Units & Measurements · Physics · JEE Advanced
MCQ (Single Correct Answer)
1
A temperature difference can generate e.m.f. in some materials. Let S be the e.m.f. produced per unit temperature difference between the ends of a wire, σ the electrical conductivity and κ the thermal conductivity of the material of the wire. Taking M, L, T, I and K as dimensions of mass, length, time, current and temperature, respectively, the dimensional formula of the quantity $Z = \frac{S^2 \sigma}{\kappa}$ is :
JEE Advanced 2025 Paper 2 Online
2
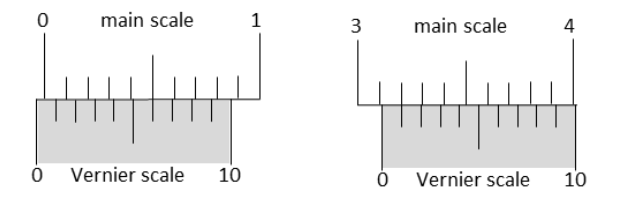
Figure 1 shows the configuration of main scale and Vernier scale before measurement. Fig. 2 shows the configuration corresponding to the measurement of diameter D of a tube. The measured value of D is:
JEE Advanced 2025 Paper 1 Online
3
A dimensionless quantity is constructed in terms of electronic charge $e$, permittivity of free space $\varepsilon_0$, Planck's constant $h$, and speed of light $c$. If the dimensionless quantity is written as $e^\alpha \varepsilon_0{ }^\beta h^\gamma c^\delta$ and $n$ is a non-zero integer, then $(\alpha, \beta, \gamma, \delta)$ is given by :
JEE Advanced 2024 Paper 1 Online
4
Young's modulus of elasticity $Y$ is expressed in terms of three derived quantities, namely, the gravitational constant $G$, Planck's constant $h$ and the speed of light $c$, as $Y=c^\alpha h^\beta G^\gamma$. Which of the following is the correct option?
JEE Advanced 2023 Paper 2 Online
5
Area of the cross-section of a wire is measured using a screw gauge. The pitch of the main scale is $0.5 \mathrm{~mm}$. The circular scale has 100 divisions and for one full rotation of the circular scale, the main scale shifts by two divisions. The measured readings are listed below.
| Measurement condition | Main scale reading | Circular scale reading |
|---|---|---|
| Two arms of gauge touching each other without wire |
0 division | 4 divisions |
| Attempt-1: With wire | 4 divisions | 20 divisions |
| Attempt-2: With wire | 4 divisions | 16 divisions |
What are the diameter and cross-sectional area of the wire measured using the screw gauge?
JEE Advanced 2022 Paper 2 Online
6
The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is
JEE Advanced 2021 Paper 1 Online
7
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
Consider the ratio $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ to be determined by measuring a dimensionless quantity $$a.$$ If the error in the measurement of $$a$$ is $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ then what is the error $$\Delta r$$ in determining $$r$$?
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
Consider the ratio $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ to be determined by measuring a dimensionless quantity $$a.$$ If the error in the measurement of $$a$$ is $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ then what is the error $$\Delta r$$ in determining $$r$$?
JEE Advanced 2018 Paper 1 Offline
8
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
JEE Advanced 2018 Paper 1 Offline
9
A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is $$\delta T = 0.01$$ seconds and he measures the depth of the well to be $$L=20$$ meters. Take the acceleration due to gravity $$g = 10m{s^{ - 2}}$$ and the velocity of sound is $$300$$ $$m{s^{ - 1}}$$. Then the fractional error in the measurement, $$\delta L/L,$$ is closest to
JEE Advanced 2017 Paper 2 Offline
10
There are two Vernier calipers both of which have 1 cm divided into 10 equal divisions on the main scale.
The Vernier scale of one of the calipers (C1) has 10 equal divisions that correspond to 9 main scale
divisions. The Vernier scale of the other caliper (C2) has 10 equal divisions that correspond to 11 main
scale divisions. The readings of the two calipers are shown in the figure. The measured values (in cm) by
calipers C1 and C2 respectively, are
JEE Advanced 2016 Paper 2 Offline
11
Match List I with List II and select the correct answer using the codes given below the lists:
Q. Coefficient of viscosity
R. Plank Constant
S. Thermal conductivity
2. [ML-1T-1]
3. [MLT-3K-1]
4. [ML2T-2K-1]
List I
P. Boltzmann ConstantQ. Coefficient of viscosity
R. Plank Constant
S. Thermal conductivity
List II
1. [ML2T-1]2. [ML-1T-1]
3. [MLT-3K-1]
4. [ML2T-2K-1]
JEE Advanced 2013 Paper 2 Offline
12
The diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero
of the Vernier scale lies between 5.10 cm and 5.15 cm of the main scale. The Vernier scale has 50 divisions
equivalent to 2.45 cm. The 24th division of the Vernier scale exactly coincides with one of the main scale
divisions. The diameter of the cylinder is
JEE Advanced 2013 Paper 1 Offline
13
In the determination of Young's modulus $$\left( {Y = {{4MLg} \over {\pi l{d^2}}}} \right)$$
by using Searle's method, a wire of length L = 2 m
and diameter d = 0.5 mm is used. For a load M = 2.5 kg, an extension l = 0.25 mm in the length of the wire
is observed. Quantities d and l are measured using a screw gauge and a micrometer, respectively. They
have the same pitch of 0.5 mm. The number of divisions on their circular scale is 100. The contributions to
the maximum probable error of the Y measurement
IIT-JEE 2012 Paper 1 Offline
14
A dense collection of equal number of electrons and positive ions is called neutral plasma. Certain solids containing
fixed positive ions surrounded by free electrons can be treated as neutral plasma. Let 'N' be the number density of
free electrons, each of mass 'm'. When the electrons are subjected to an electric field, they are displaced relatively
away from the heavy positive ions. If the electric field becomes zero, the electrons begin to oscillate about the
positive ions with a natural angular frequency '$${\omega _p}$$' which is called the plasma frequency. To sustain the oscillations,
a time varying electric field needs to be applied that has an angular frequency $$\omega $$, where a part of the energy is
absorbed and a part of it is reflected. As $$\omega $$ approaches $${\omega _p}$$ all the free electrons are set to resonance together and all
the energy is reflected. This is the explanation of high reflectivity of metals.
Taking the electronic charge as 'e' and the permittivity as $$'{\varepsilon _0}'$$. Use dimensional analysis to determine the correct expression for $${\omega _p}$$.
IIT-JEE 2011 Paper 1 Offline
15
The density of a solid ball is to be determined in an experiment. The diameter of the ball is measured with
a screw gauge, whose pitch is 0.5 mm and there are 50 divisions on the circular scale. The reading on the
main scale is 2.5 mm and that on the circular scale is 20 divisions. If the measured mass of the ball has a
relative error of 2 %, the relative percentage error in the density is
IIT-JEE 2011 Paper 2 Offline
16
A vernier calipers has 1 mm marks on the main scale. It has 20 equal divisions on the Vernier scale which match with 16 main scale divisions. For this Vernier calipers, the least count is
IIT-JEE 2010 Paper 2 Offline
17
Student I, II and III perform an experiment for measuring the acceleration due to gravity (g) using a simple pendulum. They use different length of the pendulum and/or record time for different number of oscillations. The observations area shown in the table.
Least count for length = 0.1 cm
Least count for time = 0.1 s
| Student | Length of the pendulum (cm) |
No. of oscillations (n) |
Total time for(n) oscillations (s) |
Time periods (s) |
|---|---|---|---|---|
| I | 64.0 | 8 | 128.0 | 16.0 |
| II | 64.0 | 4 | 64.0 | 16.0 |
| III | 20.0 | 4 | 36.0 | 9.0 |
If EI, EII and EIII are the percentage errors in g, i.e., $$\left(\frac{\triangle g}g\times100\right)$$ for students I, II and III, respectively,then
IIT-JEE 2008 Paper 1 Offline
18
Some physical quantities are given in Column I and some possible SI units in which these quantities may be expressed
are given in Column II. Match the physical quantities in Column I with the units in Column II.
Column I
(A) GMeMs ,
G $$ \to $$ universal gravitational constant, Me $$ \to $$ mass of the earth,
Ms $$ \to $$ mass of the Sun
(B) $${{3RT} \over M}$$,
R $$ \to $$ universal gas constant, T $$ \to $$ absolute temperature,
M $$ \to $$ molar mass
(C) $${{{F^2}} \over {{q^2}{B^2}}}$$ ,
F $$ \to $$ force, q $$ \to $$ charge, B $$ \to $$ magnetic field
(D) $${{G{M_e}} \over {{R_e}}}$$,
G $$ \to $$ universal gravitational constant,
Me $$ \to $$ mass of the earth, Re $$ \to $$ radius of the earth
Column II
(p) (volt) (coulomb) (metre)
(q) (kilogram) (metre)3 (second)−2
(r) (meter)2(second)−2
(s) (farad) (volt)2 (kg)−1
IIT-JEE 2007
19
A student performs an experiment to determine the Young's modulus of a wire, exactly 2 m long, by Searle's method. In a particular reading, the student measures the extension in the length of the wire to be 0.8 mm with an uncertainty of $$\pm0.05\;\mathrm{mm}$$ at a load of exactly 1.0 kg. The student also measures the diameter of the wire to be 0.4 mm with an uncertainty of $$\pm0.01\;\mathrm{mm}$$. Take g = 9.8 m/s2 (exact). The Young's modulus obtained from the reading is
IIT-JEE 2007 Paper 2 Offline
20
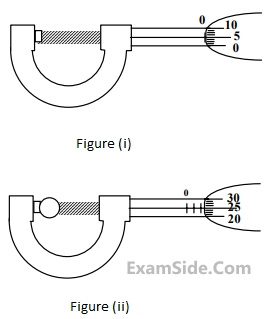
In a screw gauge, the zero of main scale coincides with the fifth division of circular scale in figure (i).The circular division of screw gauge is 50. It moves 0.5 mm on main scale in one rotation.The diameter of the ball in figure (ii) is
IIT-JEE 2006
21
A student performs an experiment for determination of $$\mathrm g\left(=\frac{4\mathrm\pi^2\mathcal l}{\mathrm T^2}\right)$$.
The error in length $$\mathcal l$$ is $$\triangle\mathcal l$$ and in the time T is $$\triangle\mathrm T$$ and n is number of times the reading is taken.The reading of g is most accurate for
IIT-JEE 2006
22
Which of the following set have different dimensions?
IIT-JEE 2005 Screening
23
A wire of length $$l = 6 \pm 0.06$$ cm and $$r = 0.5 \pm 0.005$$ cm and mass $$m = 0.3 \pm 0.003$$ gm. Maximum percentage error in density is
IIT-JEE 2004 Screening
24
Pressure depends on distance as, $$P = {\alpha \over \beta }\exp \left( { - {{\alpha z} \over {k\theta }}} \right)$$, where $$\alpha $$, $$\beta $$ are constants, z in distance, k is Boltzman's constant and $$\theta $$ is temperature. The dimention of $$\beta $$ are
IIT-JEE 2004 Screening
25
A cube has a side of length 1.2 ✕ 10-2 m. Calculate its volume.
IIT-JEE 2003 Screening
26
A quantity X is given by $${\varepsilon _0}L{{\Delta V} \over {\Delta t}}$$ where $${\varepsilon _0}$$ is the permittivity of the free space, L is a length, $${\Delta V}$$ is a potential difference and $${\Delta t}$$ is a time interval. The dimentional formula for X is the same as that of
IIT-JEE 2001 Screening
27
The dimension of $$\left( {{1 \over 2}} \right){\varepsilon _0}{E^2}$$
( $${\varepsilon _0}$$ : permittivity of free space, E electric field )
( $${\varepsilon _0}$$ : permittivity of free space, E electric field )
IIT-JEE 2000 Screening
MCQ (More than One Correct Answer)
1
Length, breadth and thickness of a strip having a uniform cross section are measured to be 10.5 cm, 0.05 mm, and 6.0 μm, respectively. Which of the following option(s) give(s) the volume of the strip in cm3 with correct significant figures:
JEE Advanced 2025 Paper 1 Online
2
A physical quantity $$\overrightarrow S $$ is defined as $$\overrightarrow S = (\overrightarrow E \times \overrightarrow B )/{\mu _0}$$, where $$\overrightarrow E $$ is electric field, $$\overrightarrow B $$ is magnetic field and $$\mu$$0 is the permeability of free space. The dimensions of $$\overrightarrow S $$ are the same as the dimensions of which of the following quantity(ies)?
JEE Advanced 2021 Paper 2 Online
3
Sometimes it is convenient to construct a system of units so that all quantities can be expressed in
terms of only one physical quantity. In one such system, dimensions of different quantities are given
in terms of a quantity X as follows: [position] = [X$$\alpha $$]; [speed] = [X$$\beta $$
]; [acceleration] = [Xp]; [linear
momentum] = [Xq]; [force] = [Xr]. Then
JEE Advanced 2020 Paper 1 Offline
4
Let us consider a system of units in which mass and angular momentum are dimensionless. If length has dimension of L, which of the following statement(s) is/are correct?
JEE Advanced 2019 Paper 1 Offline
5
In an experiment to determine the acceleration due to gravity g, the formula used for the time period of a
periodic motion is $$T = 2\pi \sqrt {{{7\left( {R - r} \right)} \over {5g}}} $$. The values of R and r are measured to be (60 $$ \pm $$ 1) mm and (10 $$ \pm $$ 1)
mm, respectively. In five successive measurements, the time period is found to be 0.52 s, 0.56 s, 0.57 s,
0.54 s and 0.59 s. The least count of the watch used for the measurement of time period is 0.01 s. Which of
the following statement(s) is(are) true?
JEE Advanced 2016 Paper 2 Offline
6
A length-scale (l) depends on the permittivity ($$\varepsilon $$) of a dielectric material, Boltzmann constant (kB), the absolute temperature (T), the number per unit volume (n) of certain charged particles, and the charge (q) carried by each of the particles. Which of the following expression(s) for I is(are) dimensionally correct?
JEE Advanced 2016 Paper 1 Offline
7
Consider a Vernier callipers in which each 1 cm on the main scale is divided into 8 equal divisions and a
screw gauge with 100 divisions on its circular scale. In the Vernier callipers, 5 divisions of the Vernier
scale coincide with 4 divisions on the main scale and in the screw gauge, one complete rotation of the
circular scale moves it by two divisions on the linear scale. Then:
JEE Advanced 2015 Paper 1 Offline
8
Planck's constant h, speed of light c and gravitational constant G are used to form a unit of length L and a
unit of mass M. Then the correct option(s) is(are)
JEE Advanced 2015 Paper 1 Offline
9
A student uses a simple pendulum of exactly 1m length to determine g, the acceleration due to gravity. He
uses a stop watch with the least count of 1 sec for this and records 40 seconds for 20 oscillations. For this
observation, which of the following statement(s) is (are) true?
IIT-JEE 2010 Paper 1 Offline
10
The SI unit of inductance, the henry can be written as
IIT-JEE 1998
11
Let [$${\mathrm\varepsilon}_\mathrm o$$] denote the dimentional formula of the permittivity of the vacuum, and [$$\mu_o$$] that of the permeability of the vacuum.If M = mass, L = length, T = time and I = electric current,
IIT-JEE 1998
12
The pairs of physical quantities that have the same dimensions is (are):
IIT-JEE 1995 Screening
13
The dimensions of the quantities in one ( or more ) of the following pairs are the same. Identify the pair(s)
IIT-JEE 1986
Numerical
1
The dimensions of a cone are measured using a scale with a least count of $2 \mathrm{~mm}$. The diameter of the base and the height are both measured to be $20.0 \mathrm{~cm}$. The maximum percentage error in the determination of the volume is _______.
JEE Advanced 2024 Paper 2 Online
2
In an experiment for determination of the focal length of a thin convex lens, the distance of the object from the lens is $10 \pm 0.1 \mathrm{~cm}$ and the distance of its real image from the lens is $20 \pm 0.2 \mathrm{~cm}$. The error in the determination of focal length of the lens is $n \%$. The value of $n$ is ______.
JEE Advanced 2023 Paper 1 Online
3
In a particular system of units, a physical quantity can be expressed in terms of the electric charge $e$, electron mass $m_{e}$, Planck's constant $h$, and Coulomb's constant $k=\frac{1}{4 \pi \epsilon_{0}}$, where $\epsilon_{0}$ is the permittivity of vacuum. In terms of these physical constants, the dimension of the magnetic field is $[B]=[e]^{\alpha}\left[m_{e}\right]^{\beta}[h]^{\gamma}[k]^{\delta}$. The value of $\alpha+\beta+\gamma+\delta$ is _______.
JEE Advanced 2022 Paper 2 Online
4
An optical bench has 1.5 m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is ..............
JEE Advanced 2019 Paper 2 Offline
5
A steel wire of diameter $$0.5$$ $$mm$$ and Young's modulus $$2 \times {10^{11}}\,\,N{m^{ - 2}}$$ carries a load of mass $$M.$$ The length of the wire with the load is $$1.0$$ $$m.A$$ vernier scale with $$10$$ divisions is attached to the end of this wire. Next to the steel wire is a reference wire to which a main scale, of least count $$1.0$$ $$mm$$ , is attached. The $$10$$ divisions of the vernier scale correspond to $$9$$ divisions of the main scale. Initially, the zero of vernier scale coincides with the zero of main scale. If the load on the steel wire is increased by $$1.2$$ $$kg,$$ the vernier scale division which coincides with a main scale division is _____________. Take $$g = 10\,m\,{s^{ - 2}}.$$ and $$\pi = 3.2.$$
JEE Advanced 2018 Paper 2 Offline
6
The energy of a system as a function of time t is given as E(t) = $${A^2}\exp \left( { - \alpha t} \right)$$, where $$\alpha = 0.2\,{s^{ - 1}}$$. The
measurement of A has an error of 1.25 %. If the error in the measurement of time is 1.50 %, the percentage
error in the value of E(t) at t = 5 s is
JEE Advanced 2015 Paper 2 Offline
7
To find the distance d over which a signal can be seen clearly in foggy conditions, a railways engineer uses
dimensional analysis and assumes that the distance depends on the mass density $$\rho $$ of the fog, intensity
(power/area) S of the light from the signal and its frequency f. The engineer finds that d is proportional to
S1/n. The value of n is
JEE Advanced 2014 Paper 1 Offline
8
During Searle's experiment, zero of the Vernier scale lies between 3.20 $$ \times $$ 10-2 m and 3.25 $$ \times $$ 10-2 m of the
main scale. The 20th division of the Vernier scale exactly coincides with one of the main scale divisions.
When an additional load of 2 kg is applied to the wire, the zero of the Vernier scale still lies between 3.20 $$ \times $$ 10-2 m and 3.25 $$ \times $$ 10-2 m of the main scale but now the 45th division of Vernier scale coincides with one of
the main scale divisions. The length of the thin metallic wire is 2 m and its cross-sectional area is 8 $$ \times $$ 10-7
m2. The least count of the Vernier scale is 1.0 $$ \times $$ 10-5 m. The maximum percentage error in the Young's
modulus of the wire is
JEE Advanced 2014 Paper 1 Offline
Subjective
1
The side of a cube is measured by vernier callipers (10 divisions of a vernier scale coincide with
9 divisions of main scale, where 1 division of main scale is 1 mm). The main scale reads 10 mm and
first division of vernier scale coincides with the main scale. Mass of the cube is 2.736 g. Find the
density of the cube in appropriate significant figures.
IIT-JEE 2005
2
In Searle's experiment, which is used to find Young's Modulus of elasticity, the diameter of experimental wire is D = 0.05 cm ( measured by a scale of least count 0.001 cm ) and length is L = 110 cm ( measured by a scale of least count 0.1 cm ). A weight of 50 N causes an extension of X = 0.125 cm (measured by a micrometer of least count 0.001 cm ). Find maximum possible error in the value of Young's modulus. Screw gauge and and meter scale are free from error.
IIT-JEE 2004
3
A screw gauge having 100 equal divisions and a pitch of length 1 mm is used to measure the diameter of a wire of length 5.6 cm. The main scale reading is 1mm and 47th circular division coincides
with the main scale. Find the curved surface area of wire in cm2 to appropriate significant figures. ( use $$\pi = {{22} \over 7}$$ )
IIT-JEE 2004
4
If nth divisions of the main scale coincide with (n+1)th divisions
of vernier scale. Given one main scale division is equal to 'a' units. Find the
least count of the vernier.
IIT-JEE 2003
5
Column - I gives the three physical quantities. Select the appropriate units for the choices given in Column - II. Some of the physical quantities may have more than one choice correct:
| Column I | Column II |
|---|---|
| Capacitance | (i) ohm-second |
| Inductance | (ii) coulomb2 - joule-1 |
| Magnetic Induction | (iii) coulomb (volt)-1 |
| (iv) newton (amp-meter)-1 | |
| (v) volt-second (ampere)-1 | |
IIT-JEE 1990
6
Match the physical quantities given in column I with dimension expressed in terms of mass (M), length (L), time (T), and charge (Q) given in column II and write the correct answer against the matched quantity in a tabular form in your answer book.
| Column I | Column II |
|---|---|
| Angular Momentum | ML2T-2 |
| Latent heat | ML2Q-2 |
| Torque | ML2T-1 |
| Capacitance | ML3T-1Q-2 |
| Inductance | M-1L-2T2Q2 |
| Resistivity | L2T-2 |
IIT-JEE 1983
7
Write the dimensions of the followings in terms of mass, time, length and charge
(i) magnetic flux
(ii) rigidity modulus
(i) magnetic flux
(ii) rigidity modulus
IIT-JEE 1982
8
A gas bubble, from an explosion under water, oscillates with a period T proportional to padbEc. Where 'P' is the static pressure, 'd' is the density of water and 'E' is the total energy of the explosion. Find the value of a, b and c.
IIT-JEE 1981
9
Give the MKS units for each of the following quantities.
(i) Young's modulus
(ii) Magnetic Induction
(iii) Power of a lens
IIT-JEE 1980
Fill in the Blanks
1
The equation of state for real gas is given by $$\left( {P + {a \over {{V^2}}}} \right)\left( {V - b} \right) = RT$$. The dimention of the constant a is ___________.
IIT-JEE 1997
2
In the formula X = 3YZ2, X and Z have dimensions of capacitance and magnetic induction respectively. The dimensions of Y in MKSQ system are _____________
IIT-JEE 1988
3
Plank' constant has dimension __________.
IIT-JEE 1985