Chemical Kinetics and Nuclear Chemistry · Chemistry · JEE Advanced
Numerical
Consider a reaction $A+R \rightarrow$ Product. The rate of this reaction is measured to be $k[A][R]$. At the start of the reaction, the concentration of $R,[R]_0$, is 10-times the concentration of $A,[A]_0$. The reaction can be considered to be a pseudo first order reaction with assumption that $k[R]=k^{\prime}$ is constant. Due to this assumption, the relative error (in %) in the rate when this reaction is $40 \%$ complete, is ___________.
[ $k$ and $k^{\prime}$ represent corresponding rate constants]
A sample initially contains only U-238 isotope of uranium. With time, some of the U-238 radioactively decays into $\mathrm{Pb}-206$ while the rest of it remains undisintegrated.
When the age of the sample is $\mathbf{P} \times 10^8$ years, the ratio of mass of $\mathrm{Pb}-206$ to that of $\mathrm{U}-238$ in the sample is found to be 7. The value of $\mathbf{P}$ is _______.
[Given: Half-life of $\mathrm{U}-238$ is $4.5 \times 10^9$ years; $\log _e 2=0.693$ ]
Consider the following reaction,
$$ 2 \mathrm{H}_2(\mathrm{~g})+2 \mathrm{NO}(\mathrm{g}) \rightarrow \mathrm{N}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) $$
which follows the mechanism given below :
$$ \begin{array}{ll} 2 \mathrm{NO}(\mathrm{g}) \stackrel{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \mathrm{N}_2 \mathrm{O}_2(\mathrm{~g}) & \text { (fast equlibrium) } \\\\ \mathrm{N}_2 \mathrm{O}_2(\mathrm{~g})+\mathrm{H}_2(\mathrm{~g}) \xrightarrow{k_2} \mathrm{~N}_2 \mathrm{O}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) & \text { (slow reaction) } \\\\ \mathrm{N}_2 \mathrm{O}(\mathrm{g})+\mathrm{H}_2(\mathrm{~g}) \xrightarrow{k_3} \mathrm{~N}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) & \text { (fast reaction) } \end{array} $$
The order of the reaction is __________.
$$2{N_2}{O_5}(g)\buildrel \Delta \over \longrightarrow 2{N_2}{O_4}(g) + {O_2}(g)$$
is started in a closed cylinder under isothermal isochoric condition at an initial pressure of 1 atm. After Y $$ \times $$ 103 s, the pressure inside the cylinder is found to be 1.45 atm. If the rate constant of the reaction is 5 $$ \times $$ 10-4s-1, assuming ideal gas behaviour, the value of Y is ...............

The rate of the reaction for [A] = 0.15 mol dm-3, [B] = 0.25 mol dm-3 and [C] = 0.15 mol dm-3 is found to be Y $$ \times $$ 10-5 mol dm-3s-1. The value of Y is .................
The activation energy of the backward reaction exceeds that of the forward reaction by $$2RT$$ (in $$J\,mo{l^{ - 1}}$$). If the pre-exponential factor of the forward reaction is $$4$$ times that of the reverse reaction, the absolute value of $$\Delta {G^ \circ }$$ (in $$J\,mo{l^{ - 1}}$$ ) for the reaction at $$300$$ $$K$$ is ____________.
(Given; $$\ln \left( 2 \right) = 0.7,RT = 2500$$ $$J\,mo{l^{ - 1}}$$ at $$300$$ $$K$$ and $$G$$ is the Gibbs energy)
$${}_{29}^{63}Cu$$ + $${}_1^1H$$ $$\to$$ $$6{}_0^1n$$ + $${}_2^4\alpha $$ + 2$${}_1^1H$$ + X
| [R] molar | 1.0 | 0.75 | 0.40 | 0.10 |
|---|---|---|---|---|
| t (min.) | 0.0 | 0.05 | 0.12 | 0.18 |
The total number of $$\alpha$$ and $$\beta$$ particles emitted in the nuclear reaction $$_{92}^{238}U \to _{82}^{214}Pb$$ is _________.
MCQ (Single Correct Answer)
Match the rate expressions in LIST-I for the decomposition of $X$ with the corresponding profiles provided in LIST-II. $X_{\mathrm{s}}$ and $\mathrm{k}$ are constants having appropriate units.
| List-I | List-II |
|---|---|
| (I) rate $=\frac{\mathrm{k}[\mathrm{X}]}{\mathrm{X}_{\mathrm{s}}+[\mathrm{X}]}$ under all possible initial concentrations of $\mathrm{X}$ |
(P)  |
| (II) rate $=\frac{k[X]}{X_{s}+[X]}$ where initial concentrations of $X$ are much less than $X_{s}$ |
(Q)  |
| (III) rate $=\frac{k[X]}{X_{s}+[X]}$ where initial concentrations of $\mathrm{X}$ are much higher than $X_{s}$ |
(R)  |
| (IV) rate $=\frac{k[X]^{2}}{X_{s}+[X]}$ where initial concentration of $X$ is much higher than $\mathrm{X}_{\mathrm{s}}$ |
(S)  |
(T)  |
The experimental value of d is found to be smaller than the estimate obtained using Graham's law. This is due to
In the reaction, P + Q $$\to$$ R + S, the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The concentration of Q varies with reaction time as shown in the figure. The overall order of the reaction is

Bombardment of aluminium by $$\alpha$$-particle leads to its artificial disintegration in two ways : (i) and (ii) as shown. Products X, Y and Z, respectively, are

Plots showing the variation of the rate constant ($$k$$) with temperature ($$T$$) are given below. The point that follows Arrhenius equation is
For a first-order reaction A $$\to$$ P, the temperature (T) dependent rate constant (k) was found to follow the equation $$\log k = - (2000){1 \over T} + 6.0$$. The pre-exponential factor A and activation energy $$E_a$$, respectively, are
Under the same reaction conditions, initial concentration of 1.386 mol dm$$^{-3}$$ of a substance becomes half in 40 seconds and 20 seconds through first order and zero order kinetics, respectively. Ratio $$\left( {{{{k_1}} \over {{k_0}}}} \right)$$ of the rate constants for first order ($$k_1$$) and zero order ($$k_0$$) of the reactions is:
MCQ (More than One Correct Answer)
$$2X + Y\buildrel k \over \longrightarrow P$$ the rate of reaction is $${{d[P]} \over {dt}} = k[X]$$. Two moles of X are mixed with one mole of Y to make 1.0 L of solution. At 50 s, 0.5 mole of Y is left in the reaction mixture. The correct statement(s) about the reaction is(are)
(Use : ln 2 = 0.693)
([P]0 is the initial concentration of P)
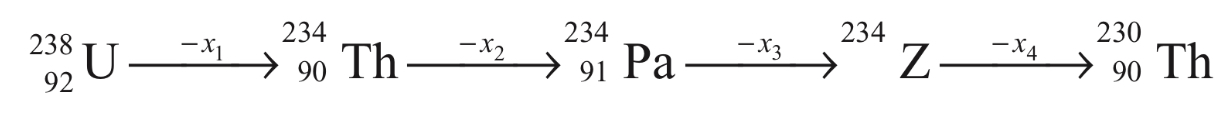
x1, x2, x3 and x4 are particles/radiation emitted by the respective isotopes. The correct option(s) is(are)
The % yield of ammonia as a function of time in the reaction
N2(g) + 3H2(g) $$\rightleftharpoons$$ 2NH3(g), $$\Delta$$H < 0 at (P, T1) is given below:

If this reactions is conducted at (P, T2), with T2 > T1, the % yield of ammonia as a function of time is represented by
9Be4 + X $$\to$$ 8Be4 + Y
(X, Y) is (are) :
2N2O5 (g) $$\to$$ 4NO2 (g) + O2 (g)
Subjective
| Observation No. | Time (in minute) | Px (in mm of Hg) |
|---|---|---|
| 1 | 0 | 800 |
| 2 | 100 | 400 |
| 3 | 200 | 200 |
(i) What is the order of the reaction to X?
(ii) Find the rate constant
(iii) Find the time for 75% completion of the reaction.
(iv) Find the total pressure when pressure of X is 700 mm of Hg
| [Ao] | [Bo] | Ro (mol L-1 s-1) | |
|---|---|---|---|
| 1 | 0.1 | 0.1 | 0.05 |
| 2 | 0.2 | 0.1 | 0.10 |
| 3 | 0.1 | 0.2 | 0.05 |
(b) Find the rate constant
2N2O5 (g) $$\to$$ 4NO2(g) + O2(g)
is a first order reaction. After 30 min. from the start of the decomposition in a closed vessel, the total pressure developed is found to be 284.5 mm of Hg and on complete decomposition, the total pressure is 584.5 mm of Hg. Calculate the rate constant of the reaction.