Heat and Thermodynamics · Physics · JEE Advanced
MCQ (More than One Correct Answer)
The efficiency of a Carnot engine operating with a hot reservoir kept at a temperature of 1000 K is 0.4 . It extracts 150 J of heat per cycle from the hot reservoir. The work extracted from this engine is being fully used to run a heat pump which has a coefficient of performance 10 . The hot reservoir of the heat pump is at a temperature of 300 K . Which of the following statements is/are correct :
In the given $P-V$ diagram, a monoatomic gas $\left(\gamma=\frac{5}{3}\right)$ is first compressed adiabatically from state $A$ to state $B$. Then it expands isothermally from state $B$ to state $C$. [Given: $\left(\frac{1}{3}\right)^{0.6} \simeq 0.5, \ln 2 \simeq 0.7$ ].

Which of the following statement(s) is(are) correct?
(Take Stefan-Boltzmann constant = 5.67 $$ \times $$ 10−8 Wm−2K−4 , Wien’s displacement constant = 2.90 $$ \times $$ 10−3 m-K, Planck’s constant = 6.63 $$ \times $$ 10−34 Js, speed of light in vacuum = 3.00 $$ \times $$ 108 ms−1)
(Given, 21.2 = 2.3; 23.2 = 9.2; R is a gas constant)


Ignoring the friction between the piston and the cylinder, the correct statements is/are

The figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously from 0 to 500 K at a constant rate. Ignoring any volume change, the following statement(s) is(are) correct to a reasonable approximation.

One mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is P0. Choose the correct option(s) from the following:

The figure shows the PV plot of an ideal gas taken through a cycle ABCDA. The part ABC is a semicircle and CDA is half of an ellipse. Then,

$$C_V$$ and $$C_P$$ denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
Numerical

Two identical plates P and Q , radiating as perfect black bodies, are kept in vacuum at constant absolute temperatures $\mathrm{T}_{\mathrm{P}}$ and $\mathrm{T}_{\mathrm{Q}}$, respectively, with $\mathrm{T}_{\mathrm{Q}}<\mathrm{T}_{\mathrm{P}}$, as shown in Fig. 1. The radiated power transferred per unit area from P to Q is $W_0$. Subsequently, two more plates, identical to P and Q , are introduced between P and Q, as shown in Fig. 2. Assume that heat transfer takes place only between adjacent plates. If the power transferred per unit area in the direction from $P$ to $Q$ (Fig. 2) in the steady state is $W_S$, then the ratio $\frac{W_0}{W_S}$ is ________.

The specific heat capacity of a substance is temperature dependent and is given by the formula $C=k T$, where $k$ is a constant of suitable dimensions in SI units, and $T$ is the absolute temperature. If the heat required to raise the temperature of $1 \mathrm{~kg}$ of the substance from $-73^{\circ} \mathrm{C}$ to $27^{\circ} \mathrm{C}$ is $n k$, the value of $n$ is ________.
[Given: $0 \mathrm{~K}=-273{ }^{\circ} \mathrm{C}$.]

The value of X is _______________.

The value of Y is _______________.
(take the acceleration due to gravity = 10 ms−2 and the universal gas constant = 8.3 J mol−1K−1).


A metal rod AB of length 10x has its one end A in ice at 0$$^\circ$$C and the other end B in water at 100$$^\circ$$C. If a point P on the rod is maintained at 400$$^\circ$$C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540 cal/g and latent heat of melting of ice is 80 cal/g. If the point P is at a distance of $$\lambda x$$ from the ice end A, find the value of $$\lambda$$. (Neglect any heat loss to the surrounding.)
MCQ (Single Correct Answer)
One mole of a monatomic ideal gas undergoes the cyclic process $\mathrm{J} \rightarrow \mathrm{K} \rightarrow \mathrm{L} \rightarrow \mathrm{M} \rightarrow \mathrm{J}$, as shown in the P-T diagram.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
[ $\mathcal{R}$ is the gas constant.]
| List-I | List-II |
|---|---|
| (P) Work done in the complete cyclic process | (1) $RT_0 - 4RT_0 \ln 2$ |
| (Q) Change in the internal energy of the gas in the process JK | (2) $0$ |
| (R) Heat given to the gas in the process KL | (3) $3RT_0$ |
| (S) Change in the internal energy of the gas in the process MJ | (4) $-2RT_0 \ln 2$ |
| (5) $-3RT_0 \ln 2$ |
[Given: Wien's constant as $2.9 \times 10^{-3} \mathrm{~m}-\mathrm{K}$ and $\frac{h c}{e}=1.24 \times 10^{-6} \mathrm{~V}-\mathrm{m}$ ]
| List - I | List - II |
|---|---|
| (P) $2000 \mathrm{~K}$ | (1) The radiation at peak wavelength can lead to emission of photoelectrons from a metal of work function $4 \mathrm{eV}$. |
| (Q) $3000 \mathrm{~K}$ | (2) The radiation at peak wavelength is visible to human eye. |
| (R) $5000 \mathrm{~K}$ | (3) The radiation at peak emission wavelength will result in the widest central maximum of a single slit diffraction. |
| (S) $10000 \mathrm{~K}$ | (4) The power emitted per unit area is $1 / 16$ of that emitted by a blackbody at temperature $6000 \mathrm{~K}$. |
| (5) The radiation at peak emission wavelength can be used to image human bones. |
List I describes thermodynamic processes in four different systems. List II gives the magnitudes (either exactly or as a close approximation) of possible changes in the internal energy of the system due to the process.
| List-I | List-II |
|---|---|
| (I) $10^{-3} \mathrm{~kg}$ of water at $100^{\circ} \mathrm{C}$ is converted to steam at the same temperature, at a pressure of $10^{5} \mathrm{~Pa}$. The volume of the system changes from $10^{-6} \mathrm{~m}^{3}$ to $10^{-3} \mathrm{~m}^{3}$ in the process. Latent heat of water $=2250\, \mathrm{~kJ} / \mathrm{kg}$. |
(P) $2 \mathrm{~kJ}$ |
| (II) $0.2$ moles of a rigid diatomic ideal gas with volume $V$ at temperature $500 \mathrm{~K}$ undergoes an isobaric expansion to volume $3 \mathrm{~V}$. Assume $R=8.0 \mathrm{Jmol}^{-1} \mathrm{~K}^{-1}$. |
(Q) $7 k J$ |
| (III) One mole of a monatomic ideal gas is compressed adiabatically from volume $V=\frac{1}{3} \mathrm{~m}^{3}$ and pressure $2 \mathrm{kPa}$ to volume $\frac{V}{8}$. |
(R) $4 \mathrm{~kJ}$ |
| (IV) Three moles of a diatomic ideal gas whose molecules can vibrate, is given $9 \mathrm{~kJ}$ of heat and undergoes isobaric expansion. |
(S) $5 \mathrm{~kJ}$ |
| (T) $3 \mathrm{~kJ}$ |
Which one of the following options is correct?

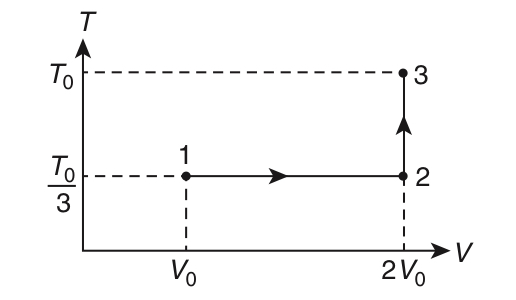
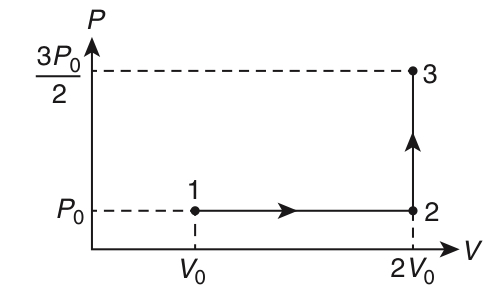
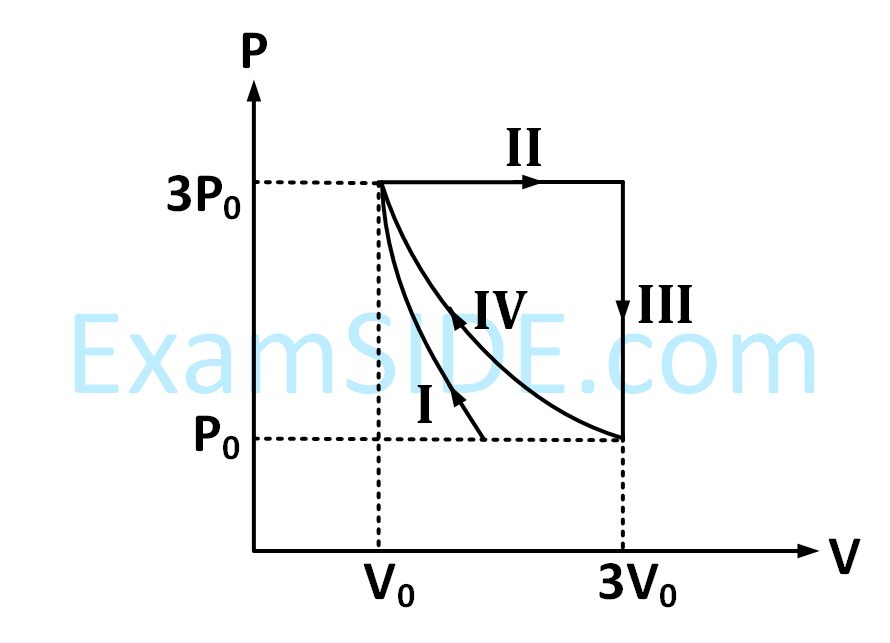
| LIST - I | LIST - II | ||
|---|---|---|---|
| P. | In process I | 1. | Work done by the gas is zero |
| Q. | In process II | 2. | Temperature of the gas remains unchanged |
| R. | In process III | 3. | No heat is exchanged between the gas and its surroundings |
| S. | In process IV | 4. | Work done by the gas is 6P0V0 |
$$\Delta U = \Delta Q - P\Delta V$$?
The temperature of water fed into the device cannot exceed 30°C and the entire stored 120 litres of water is initially cooled to 10°C. The entire system is thermally insulated. The minimum value of P (in watts) for which the device can be operated for 3 hours is :
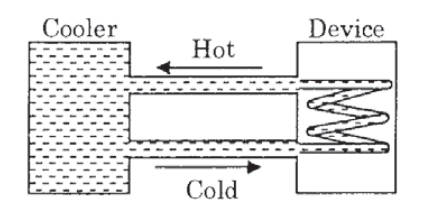
(Specific heat of water is 4.2 kJ kg−1 K−1 and the density of water is 1000 kg m−3)
Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gases will be
Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. Then total work done by the gases till the time they achieve equilibrium will be
One mole of a monatomic ideal gas is taken along two cyclic processes E $$\to$$ F $$\to$$ G $$\to$$ E and E $$\to$$ F $$\to$$ H $$\to$$ E as shown in the PV diagram. The processes involved are purely isochoric, isobaric, isothermal or adiabatic.

Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists :
| List I | List II | ||
|---|---|---|---|
| P. | $$G \to E$$ |
1. | 160$${P_0}{V_0}$$ln2 |
| Q. | $$G \to H$$ |
2. | 36$${P_0}{V_0}$$ |
| R. | $$F \to H$$ |
3. | 24$${P_0}{V_0}$$ |
| S. | $$F \to G$$ |
4. | 31$${P_0}{V_0}$$ |
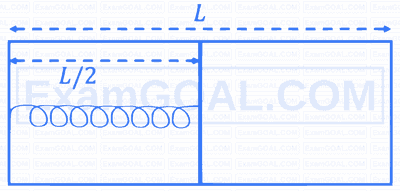
Two rectangular blocks, having identical dimensions, can be arranged in either configuration-I or configuration-II as shown in the figure. One of the blocks has thermal conductivity $$\kappa $$ and the other 2$$\kappa $$. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9 s to transport a certain amount of heat from the hot end to the cold end in configuration-I. The time to transport the same amount of heat in configuration-II is

Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surfaces and have very high thermal conductively. The first and third plates are maintained at temperatures 2T and 3T, respectively. The temperature of the middle (i.e. second) plate under steady state condition is
One mole of a monatomic gas is taken through a cycle ABCDA as shown in the PV diagram. Column II give the characteristics involved in the cycle. Match them with each of the processes given in Column I.

| Column I | Column II | ||
|---|---|---|---|
| (A) | Process A$$ \to $$ B | (P) | Internal energy decreases. |
| (B) | Process B$$ \to $$C | (Q) | Internal energy increase. |
| (C) | Process C$$ \to $$D | (R) | Heat is lost. |
| (D) | Process D$$ \to $$A | (S) | Heat is gained. |
| (T) | Work is done on the gas. |
Column II gives certain systems undergoing a process. Column I suggests changes in some of the parameters related to the system. Match the statements in Column I to the appropriate process(es) from Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | The energy of the system is increased. | (P) | System : A capacitor, initially uncharged. Process : It is connected to a battery. |
| (B) | Mechanical energy is provided to the system, which is converted into energy of random motion of its parts. | (Q) | System : A gas in an adiabatic container filled with an adiabatic piston. Process : The gas is compressed by pushing the piston. |
| (C) | Internal energy of the system is converted into its mechanical energy. | (R) | System : A gas in a rigid container. Process : The gas gets cooled due to colder atmosphere surrounding it. |
| (D) | Mass of the system is decreased. | (S) | System : A heavy nucleus, initially at rest. Process : The nucleus fissions into two fragments of nearly equal masses and some neutrons are emitted. |
| (T) | System : A resistive wire loop. Process : The loop is placed in a time varying magnetic field perpendicular to its plane. |
Column I contains a list of processes involving expansion of an ideal gas. Match this with Column II describing the thermodynamic change during this process. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | An insulated container has two chambers separated by a valve. Chamber I contains an ideal gas and the Chamber II has vacuum. The valve is opened. |
(P) | The temperature of the gas decreases |
| (B) | An ideal monatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^2}$$, where V is the volume of the gas | (Q) | The temperature of the gas increase or remains constant. |
| (C) | An ideal monoatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^{4/3}}$$, where V is its volume | (R) | The gas loses heat |
| (D) | An ideal monoatomic gas expands such that its pressure P and volume V follows the behaviour shown in the graph |
(S) | The gas gains heat |
An ideal gas is expanding such that PT$$^2$$ = constant. The coefficient of volume expansion of the gas is
STATEMENT 1
The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and its volume.
Because
STATEMENT 2
The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.