Parabola · Mathematics · JEE Advanced
MCQ (More than One Correct Answer)
1
Let $A_1, B_1, C_1$ be three points in the $x y$-plane. Suppose that the lines $A_1 C_1$ and $B_1 C_1$ are tangents to the curve $y^2=8 x$ at $A_1$ and $B_1$, respectively. If $O=(0,0)$ and $C_1=(-4,0)$, then which of the following statements is (are) TRUE?
JEE Advanced 2024 Paper 2 Online
2
Consider the parabola $$y^{2}=4 x$$. Let $$S$$ be the focus of the parabola. A pair of tangents drawn to the parabola from the point $$P=(-2,1)$$ meet the parabola at $$P_{1}$$ and $$P_{2}$$. Let $$Q_{1}$$ and $$Q_{2}$$ be points on the lines $$S P_{1}$$ and $$S P_{2}$$ respectively such that $$P Q_{1}$$ is perpendicular to $$S P_{1}$$ and $$P Q_{2}$$ is perpendicular to $$S P_{2}$$. Then, which of the following is/are TRUE?
JEE Advanced 2022 Paper 1 Online
3
Let E denote the parabola y2 = 8x. Let P = ($$-$$2, 4), and let Q and Q' be two distinct points on E such that the lines PQ and PQ' are tangents to E. Let F be the focus of E. Then which of the following statements is(are) TRUE?
JEE Advanced 2021 Paper 2 Online
4
If a chord, which is not a tangent, of the parabola y2 = 16x has the equation 2x + y = p, and mid-point (h, k), then which of the following is(are) possible value(s) of p, h and k?
JEE Advanced 2017 Paper 1 Offline
5
Let $$P$$ be the point on the parabola $${y^2} = 4x$$ which is at the shortest distance from the center $$S$$ of the circle $${x^2} + {y^2} - 4x - 16y + 64 = 0$$. Let $$Q$$ be the point on the circle dividing the line segment $$SP$$ internally. Then
JEE Advanced 2016 Paper 2 Offline
6
The circle $${C_1}:{x^2} + {y^2} = 3,$$ with centre at $$O$$, intersects the parabola $${x^2} = 2y$$ at the point $$P$$ in the first quadrant, Let the tangent to the circle $${C_1}$$, at $$P$$ touches other two circles $${C_2}$$ and $${C_3}$$ at $${R_2}$$ and $${R_3}$$, respectively. Suppose $${C_2}$$ and $${C_3}$$ have equal radil $${2\sqrt 3 }$$ and centres $${Q_2}$$ and $${Q_3}$$, respectively. If $${Q_2}$$ and $${Q_3}$$ lie on the $$y$$-axis, then
JEE Advanced 2016 Paper 1 Offline
7
Let $$P$$ and $$Q$$ be distinct points on the parabola $${y^2} = 2x$$ such that a circle with $$PQ$$ as diameter passes through the vertex $$O$$ of the parabola. If $$P$$ lies in the first quadrant and the area of the triangle $$\Delta OPQ$$ is $${3\sqrt 2 ,}$$ then which of the following is (are) the coordinates of $$P$$?
JEE Advanced 2015 Paper 1 Offline
8
Let L be a normal to the parabola y2 = 4x. If L passes through the point (9, 6), then L is given by
IIT-JEE 2011 Paper 2 Offline
9
Let $$A$$ and $$B$$ be two distinct points on the parabola $${y^2} = 4x$$. If the axis of the parabola touches a circle of radius $$r$$ having $$AB$$ as its diameter, then the slope of the line joining $$A$$ and $$B$$ can be
IIT-JEE 2010 Paper 1 Offline
10
The tangent $$PT$$ and the normal $$PN$$ to the parabola $${y^2} = 4ax$$ at a point $$P$$ on it meet its axis at points $$T$$ and $$N$$, respectively. The locus of the centroid of the triangle $$PTN$$ is a parabola whose
IIT-JEE 2009 Paper 2 Offline
11
The equations of the common tangents to the parabola $$y = {x^2}$$ and $$y = - {\left( {x - 2} \right)^2}$$ is/are
IIT-JEE 2006
Numerical
1
A normal with slope $\frac{1}{\sqrt{6}}$ is drawn from the point $(0,-\alpha)$ to the parabola $x^2=-4 a y$, where $a>0$. Let $L$ be the line passing through $(0,-\alpha)$ and parallel to the directrix of the parabola. Suppose that $L$ intersects the parabola at two points $A$ and $B$. Let $r$ denote the length of the latus rectum and $s$ denote the square of the length of the line segment $A B$. If $r: s=1: 16$, then the value of $24 a$ is _______.
JEE Advanced 2024 Paper 2 Online
2
Suppose that the foci of the ellipse $${{{x^2}} \over 9} + {{{y^2}} \over 5} = 1$$ are $$\left( {{f_1},0} \right)$$ and $$\left( {{f_2},0} \right)$$ where $${{f_1} > 0}$$ and $${{f_2} < 0}$$. Let $${P_1}$$ and $${P_2}$$ be two parabolas with a common vertex at $$(0,0)$$ and with foci at $$\left( {{f_1},0} \right)$$ and $$\left( 2{{f_2},0} \right)$$, respectively. Let $${T_1}$$ be a tangent to $${P_1}$$ which passes through $$\left( 2{{f_2},0} \right)$$ and $${T_2}$$ be a tangent to $${P_2}$$ which passes through $$\left( {{f_1},0} \right)$$. If $${m_1}$$ is the slope of $${T_1}$$ and $${m_2}$$ is the slope of $${T_2}$$, then the value of $$\left( {{1 \over {m_1^2}} + m_2^2} \right)$$ is
JEE Advanced 2015 Paper 2 Offline
3
If the normals of the parabola $${y^2} = 4x$$ drawn at the end points of its latus rectum are tangents to the circle $${\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = {r^2}$$, then the value of $${r^2}$$ is
JEE Advanced 2015 Paper 1 Offline
4
Let the curve $$C$$ be the mirror image of the parabola $${y^2} = 4x$$ with respect to the line $$x+y+4=0$$. If $$A$$ and $$B$$ are the points of intersection of $$C$$ with the line $$y=-5$$, then the distance between $$A$$ and $$B$$ is
JEE Advanced 2015 Paper 1 Offline
5
Let $$S$$ be the focus of the parabola $${y^2} = 8x$$ and let $$PQ$$ be the common chord of the circle $${x^2} + {y^2} - 2x - 4y = 0$$ and the given parabola. The area of the triangle $$PQS$$ is
IIT-JEE 2012 Paper 1 Offline
6
Consider the parabola $${y^2} = 8x$$. Let $${\Delta _1}$$ be the area of the triangle formed by the end points of its latus rectum and the point $$P\left( {{1 \over 2},2} \right)$$ on the parabola and $${\Delta _2}$$ be the area of the triangle formed by drawing tangents at $$P$$ and at the end points of the latus rectum. Then $${{{\Delta _1}} \over {{\Delta _2}}}$$ is
IIT-JEE 2011 Paper 1 Offline
MCQ (Single Correct Answer)
1
Let $P$ be a point on the parabola $y^2=4 a x$, where $a>0$. The normal to the parabola at $P$ meets the $x$-axis at a point $Q$. The area of the triangle $P F Q$, where $F$ is the focus of the parabola, is 120 . If the slope $m$ of the normal and $a$ are both positive integers, then the pair $(a, m)$ is
JEE Advanced 2023 Paper 1 Online
2
Let a, b and $$\lambda $$ be positive real numbers. Suppose P is an end point of the latus return of the
parabola y2 = 4$$\lambda $$x, and suppose the ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
parabola y2 = 4$$\lambda $$x, and suppose the ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
JEE Advanced 2020 Paper 1 Offline
3
Let the circles
C1 : x2 + y2 = 9 and C2 : (x $$-$$ 3)2 + (y $$-$$ 4)2 = 16, intersect at the points X and Y. Suppose that another circle C3 : (x $$-$$ h)2 + (y $$-$$ k)2 = r2 satisfies the following conditions :
(i) Centre of C3 is collinear with the centres of C1 and C2.
(ii) C1 and C2 both lie inside C3 and
(iii) C3 touches C1 at M and C2 at N.
Let the line through X and Y intersect C3 at Z and W, and let a common tangent of C1 and C3 be a tangent to the parabola x2 = 8$$\alpha $$y.
There are some expression given in the List-I whose values are given in List-II below.
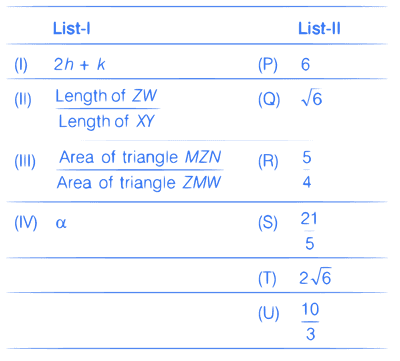
Which of the following is the only INCORRECT combination?
C1 : x2 + y2 = 9 and C2 : (x $$-$$ 3)2 + (y $$-$$ 4)2 = 16, intersect at the points X and Y. Suppose that another circle C3 : (x $$-$$ h)2 + (y $$-$$ k)2 = r2 satisfies the following conditions :
(i) Centre of C3 is collinear with the centres of C1 and C2.
(ii) C1 and C2 both lie inside C3 and
(iii) C3 touches C1 at M and C2 at N.
Let the line through X and Y intersect C3 at Z and W, and let a common tangent of C1 and C3 be a tangent to the parabola x2 = 8$$\alpha $$y.
There are some expression given in the List-I whose values are given in List-II below.
Which of the following is the only INCORRECT combination?
JEE Advanced 2019 Paper 2 Offline
4
Let the circle C1 : x2 + y2 = 9 and C2 : (x $$-$$ 3)2 + (y $$-$$ 4)2 = 16, intersect at the points X and Y. Suppose that another circle C3 : (x $$-$$ h)2 + (y $$-$$ k)2 = r2 satisfies the following conditions :
(i) centre of C3 is collinear with the centers of C1 and C2.
(ii) C1 and C2 both lie inside C3, and
(iii) C3 touches C1 at M and C2 at N.
Let the line through X and Y intersect C3 at Z and W, and let a common tangent of C1 and C3 be a tangent to the parabola x2 = 8$$\alpha $$y.
There are some expression given in the List-I whose values are given in List-II below.
Which of the following is the only CORRECT combination?
(i) centre of C3 is collinear with the centers of C1 and C2.
(ii) C1 and C2 both lie inside C3, and
(iii) C3 touches C1 at M and C2 at N.
Let the line through X and Y intersect C3 at Z and W, and let a common tangent of C1 and C3 be a tangent to the parabola x2 = 8$$\alpha $$y.
There are some expression given in the List-I whose values are given in List-II below.
Which of the following is the only CORRECT combination?
JEE Advanced 2019 Paper 2 Offline
5
If a tangent to a suitable conic (Column 1) is found to be y = x + 8 and its point of contact is (8, 16), then which of the following options is the only CORRECT combination?
JEE Advanced 2017 Paper 1 Offline
6
Let $$a, r, s, t$$ be nonzero real numbers. Let $$P\,\,\left( {a{t^2},2at} \right),\,\,Q,\,\,\,R\,\,\left( {a{r^2},2ar} \right)$$ and $$S\,\,\left( {a{s^2},2as} \right)$$ be distinct points on the parabola $${y^2} = 4ax$$. Suppose that $$PQ$$ is the focal chord and lines $$QR$$ and $$PK$$ are parallel, where $$K$$ is the point $$(2a,0)$$
The value of $$r$$ is
JEE Advanced 2014 Paper 2 Offline
7
Let $$a, r, s, t$$ be nonzero real numbers. Let $$P\,\,\left( {a{t^2},2at} \right),\,\,Q,\,\,\,R\,\,\left( {a{r^2},2ar} \right)$$ and $$S\,\,\left( {a{s^2},2as} \right)$$ be distinct points on the parabola $${y^2} = 4ax$$. Suppose that $$PQ$$ is the focal chord and lines $$QR$$ and $$PK$$ are parallel, where $$K$$ is the point $$(2a,0)$$
If $$st=1$$, then the tangent at $$P$$ and the normal at $$S$$ to the parabola meet at a point whose ordinate is
JEE Advanced 2014 Paper 2 Offline
8
A line $$L:y=mx+3$$ meets $$y$$-axis at R$$(0, 3)$$ and the arc of the parabola $${y^2} = 16x,$$ $$0 \le y \le 6$$ at the point $$F\left( {{x_0},{y_0}} \right)$$. The tangent to the parabola at $$F\left( {{x_0},{y_0}} \right)$$ intersects the $$y$$-axis at $$G\left( {0,{y_1}} \right)$$. The slope $$m$$ of the line $$L$$ is chosen such that the area of the triangle $$EFG$$ has a local maximum.
Match List $$I$$ with List $$II$$ and select the correct answer using the code given below the lists:
List $$I$$
P.$$\,\,\,m = $$
Q.$$\,\,\,$$Maximum area of $$\Delta EFG$$ is
R.$$\,\,\,$$ $${y_0} = $$
S.$$\,\,\,$$ $${y_1} = $$
List $$II$$
1.$$\,\,\,$$ $${1 \over 2}$$
2.$$\,\,\,$$ $$4$$
3.$$\,\,\,$$ $$2$$
4.$$\,\,\,$$ $$1$$
JEE Advanced 2013 Paper 2 Offline
9
Let $$PQ$$ be a focal chord of the parabola $${y^2} = 4ax$$. The tangents to the parabola at $$P$$ and $$Q$$ meet at a point lying on the line $$y=2x+a$$, $$a>0$$.
Length of chord $$PQ$$ is
JEE Advanced 2013 Paper 2 Offline
10
Let $$PQ$$ be a focal chord of the parabola $${y^2} = 4ax$$. The tangents to the parabola at $$P$$ and $$Q$$ meet at a point lying on the line $$y=2x+a$$, $$a>0$$.
If chord $$PQ$$ subtends an angle $$\theta $$ at the vertex of $${y^2} = 4ax$$, then tan $$\theta = $$
JEE Advanced 2013 Paper 2 Offline
11
Let $$(x, y)$$ be any point on the parabola $${y^2} = 4x$$. Let $$P$$ be the point that divides the line segment from $$(0, 0)$$ to $$(x, y)$$ in the ratio $$1 : 3$$. Then the locus of $$P$$ is
IIT-JEE 2011 Paper 2 Offline
12
The locus of the orthocentre of the triangle formed by the lines
$$(1 + p)x - py + p(1 + p) = 0,
$$
$$(1 + q)x - qy + q(1 + q) = 0$$
and $$y = 0$$, where $$p \ne q$$, is :
IIT-JEE 2009 Paper 2 Offline
13
STATEMENT-1: The curve $$y = {{ - {x^2}} \over 2} + x + 1$$ is symmetric with respect to the line $$x=1$$. because
STATEMENT-2: A parabola is symmetric about its axis.
IIT-JEE 2007
14
Consider the circle $${x^2} + {y^2} = 9$$ and the parabola $${y^2} = 8x$$. They intersect at $$P$$ and $$Q$$ in the first and the fourth quadrants, respectively. Tangent to the circle at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$R$$ and tangents to the parabola at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$S$$.
The radius of the circumcircle of the triangle $$PRS$$ is
IIT-JEE 2007
15
Consider the circle $${x^2} + {y^2} = 9$$ and the parabola $${y^2} = 8x$$. They intersect at $$P$$ and $$Q$$ in the first and the fourth quadrants, respectively. Tangent to the circle at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$R$$ and tangents to the parabola at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$S$$.
The radius of the incircle of the triangle $$PQR$$ is
IIT-JEE 2007
16
Consider the circle $${x^2} + {y^2} = 9$$ and the parabola $${y^2} = 8x$$. They intersect at $$P$$ and $$Q$$ in the first and the fourth quadrants, respectively. Tangent to the circle at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$R$$ and tangents to the parabola at $$P$$ and $$Q$$ intersect the $$x$$-axis at $$S$$.
The ratio of the areas of the triangles $$PQS$$ and $$PQR$$ is
IIT-JEE 2007
17
The axis of a parabola is along the line $$y = x$$ and the distances of its vertex and focus from origin are $$\sqrt 2 $$ and $$2\sqrt 2 $$ respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
IIT-JEE 2006
18
Match the following : $$(3, 0)$$ is the pt. from which three normals are drawn to the parabola $${y^2} = 4x$$ which meet the parabola in the points $$P, Q $$ and $$R$$. Then
Column $${\rm I}$$
(A) Area of $$\Delta PQR$$
(B) Radius of circumcircle of $$\Delta PQR$$
(C) Centroid of $$\Delta PQR$$
(D) Circumcentre of $$\Delta PQR$$
Column $${\rm I}$$$${\rm I}$$
(p) $$2$$
(q) $$5/2$$
(r) $$(5/2, 0)$$
(s) $$(2/3, 0)$$
IIT-JEE 2006
19
Tangent to the curve $$y = {x^2} + 6$$ at a point $$(1, 7)$$ touches the circle $${x^2} + {y^2} + 16x + 12y + c = 0$$ at a point $$Q$$. Then the coordinates of $$Q$$ are
IIT-JEE 2005 Screening
20
The angle between the tangents drawn from the point $$(1, 4)$$ to the parabola $${y^2} = 4x$$ is
IIT-JEE 2004 Screening
21
The focal chord to $${y^2} = 16x$$ is tangent to $${\left( {x - 6} \right)^2} + {y^2} = 2,$$ then the possible values of the slope of the chord, are
IIT-JEE 2003 Screening
22
The locus of the mid-point of the line segment joining the focus to a moving point on the parabola $${y^2} = 4ax$$ is another parabola with directrix
IIT-JEE 2002 Screening
23
The equation of the common tangent to the curves $${y^2} = 8x$$ and $$xy = - 1$$ is
IIT-JEE 2002 Screening
24
The equation of the directrix of the parabola $${y^2} + 4y + 4x + 2 = 0$$
IIT-JEE 2001 Screening
25
The equation of the common tangent touching the circle $${\left( {x - 3} \right)^2} + {y^2} = 9$$ and the parabola $${y^2} = 4x$$ above the $$x$$-axis is
IIT-JEE 2001 Screening
26
If the line $$x - 1 = 0$$ is the directrix of the parabola $${y^2} - kx + 8 = 0,$$ then one of the values of $$k$$ is
IIT-JEE 2000 Screening
27
If $$x + y = k$$ is normal to $${y^2} = 12x,$$ then $$k$$ is
IIT-JEE 2000 Screening
28
The curve described parametrically by $$x = {t^2} + t + 1,$$ $$y = {t^2} - t + 1 $$ represents
IIT-JEE 1999
29
Consider a circle with its centre lying on the focus of the parabola $${y^2} = 2px$$ such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is
IIT-JEE 1995 Screening
Subjective
1
Tangent is drawn to parabola $${y^2} - 2y - 4x + 5 = 0$$ at a point $$P$$ which cuts the directrix at the point $$Q$$. $$A$$ point $$R$$ is such that it divides $$QP$$ externally in the ratio $$1/2:1$$. Find the locus of point $$R$$
IIT-JEE 2004
2
Normals are drawn from the point $$P$$ with slopes $${m_1}$$, $${m_2}$$, $${m_3}$$ to the parabola $${y^2} = 4x$$. If locus of $$P$$ with $${m_1}$$ $${m_2}$$$$ = \alpha $$ is a part of the parabola itself then find $$\alpha $$.
IIT-JEE 2003
3
Let $${C_1}$$ and $${C_2}$$ be respectively, the parabolas $${x^2} = y - 1$$ and $${y^2} = x - 1$$. Let $$P$$ be any point on $${C_1}$$ and $$Q$$ be any point on $${C_2}$$. Let $${P_1}$$ and $${Q_1}$$ be the reflections of $$P$$ and $$Q$$, respectively, with respect to the line $$y=x$$. Prove that $${P_1}$$ lies on $${C_2}$$, $${Q_1}$$ lies on $${C_1}$$ and $$PQ \ge $$ min $$\left\{ {P{P_1},Q{Q_1}} \right\}$$. Hence or otherwise determine points $${P_0}$$ and $${Q_0}$$ on the parabolas $${C_1}$$ and $${C_2}$$ respectively such that $${P_0}{Q_0} \le PQ$$ for all pairs of points $$(P,Q)$$ with $$P$$ on $${C_1}$$ and $$Q$$ on $${C_2}$$.
IIT-JEE 2000
4
From a point $$A$$ common tangents are drawn to the circle $${x^2} + {y^2} = {a^2}/2$$ and parabola $${y^2} = 4ax$$. Find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola.
IIT-JEE 1996
5
Points $$A, B$$ and $$C$$ lie on the parabola $${y^2} = 4ax$$. The tangents to the parabola at $$A, B$$ and $$C$$, taken in pairs, intersect at points $$P, Q$$ and $$R$$. Determine the ratio of the areas of the triangles $$ABC$$ and $$PQR$$.
IIT-JEE 1996
6
Show that the locus of a point that divides a chord of slope $$2$$ of the parabola $${y^2} = 4x$$ internally in the ratio $$1:2$$ is a parabola. Find the vertex of this parabola.
IIT-JEE 1995
7
Through the vertex $$O$$ of parabola $${y^2} = 4x$$, chords $$OP$$ and $$OQ$$ are drawn at right angles to one another . Show that for all positions of $$P$$, $$PQ$$ cuts the axis of the parabola at a fixed point. Also find the locus of the middle point of $$PQ$$.
IIT-JEE 1994
8
Three normals are drawn from the point $$(c, 0)$$ to the curve $${y^2} = x.$$ Show that $$c$$ must be greater than $$1/2$$. One normal is always the $$x$$-axis. Find $$c$$ for which the other two normals are perpendicular to each other.
IIT-JEE 1991
9
$$A$$ is point on the parabola $${y^2} = 4ax$$. The normal at $$A$$ cuts the parabola again at point $$B$$. If $$AB$$ subtends a right angle at the vertex of the parabola. Find the slope of $$AB$$.
IIT-JEE 1982
10
Suppose that the normals drawn at three different points on the parabola $${y^2} = 4x$$ pass through the point $$(h, k)$$. Show that $$h>2$$.
IIT-JEE 1981