ExamSIDE (Powered by ExamGOAL)
Questions
PREVIOUS NEXT
1
GATE ECE 2004
MCQ (Single Correct Answer)
+2
-0.6
Consider the Bode magnitude plot shown in figure. The transfer function H(s) is GATE ECE 2004 Control Systems - Frequency Response Analysis Question 37 English
A
$${{\left( {s + 10} \right)} \over {\left( {s + 1} \right)\left( {s + 100} \right)}}$$
B
$${{10\left( {s + 1} \right)} \over {\left( {s + 10} \right)\left( {s + 100} \right)}}$$
C
$${{{{10}^2}\left( {s + 1} \right)} \over {\left( {s + 10} \right)\left( {s + 100} \right)}}$$
D
$${{{{10}^3}\left( {s + 100} \right)} \over {\left( {s + 1} \right)\left( {s + 10} \right)}}$$
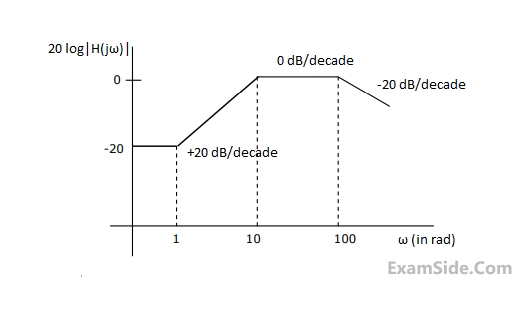
2
GATE ECE 2004
MCQ (Single Correct Answer)
+2
-0.6
A system has poles at 0.01 Hz, 1Hz and 80 Hz; zeroes at 5hz, 100 Hz and 200 Hz. The approximate phase of the system response at 20 Hz is
A
$$ - {90^0}$$
B
$$ {0^0}$$
C
$$ {90^0}$$
D
$$ {-180^0}$$
3
GATE ECE 2003
MCQ (Single Correct Answer)
+2
-0.6
The approximate Bode magnitude plot of a minimum-phase system is shown in figure. The transfer function of the system is GATE ECE 2003 Control Systems - Frequency Response Analysis Question 38 English
A
$${10^8}{{{{\left( {s + 0.1} \right)}^3}} \over {{{\left( {s + 10} \right)}^2}\left( {s + 100} \right)}}$$
B
$${10^7}{{{{\left( {s + 0.1} \right)}^3}} \over {{{\left( {s + 10} \right)}}\left( {s + 100} \right)}}$$
C
$${10^8}{{{{\left( {s + 0.1} \right)}^2}} \over {{{\left( {s + 10} \right)}^2}\left( {s + 100} \right)}}$$
D
$${10^9}{{{{\left( {s + 0.1} \right)}^3}} \over {\left( {s + 10} \right){{\left( {s + 100} \right)}^2}}}$$
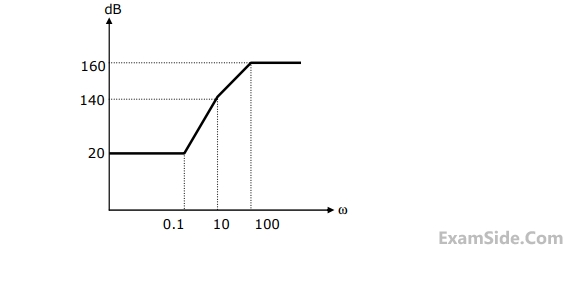
4
GATE ECE 2003
MCQ (Single Correct Answer)
+2
-0.6
The gain margin and the phase margin of a feedback system with G(s)H(s)=$${s \over {{{\left( {s + 100} \right)}^3}}}$$ are
A
0 dB, $${0^0}$$
B
$$\infty ,\infty $$
C
$$\infty ,{0^0}$$
D
88.5 dB, $$\infty $$
PREVIOUS NEXT
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
State Equations For Networks Network Elements Network Theorems Two Port Networks Transient Response Sinusoidal Steady State Response Network Graphs Miscellaneous
Control Systems
Basic of Control Systems Signal Flow Graph and Block Diagram Time Response Analysis Stability Root Locus Diagram Frequency Response Analysis Compensators State Space Analysis
Digital Circuits
Number System and Code Convertions Boolean Algebra Logic Gates Combinational Circuits Sequential Circuits Semiconductor Memories Logic Families Analog to Digital and Digital to Analog Converters
General Aptitude
Numerical Ability Logical Reasoning Verbal Ability
Electronic Devices and VLSI
PN Junction Semiconductor Physics IC Basics and MOSFET BJT and FET
Analog Circuits
Bipolar Junction Transistor FET and MOSFET Oscillators Operational Amplifier 555 Timer Frequency Response Diodes Feedback Amplifier Power Amplifier
Engineering Mathematics
Linear Algebra Calculus Vector Calculus Complex Variable Probability and Statistics Differential Equations Numerical Methods Transform Theory
Microprocessors
Pin Details of 8085 and Interfacing with 8085 Instruction Set and Programming with 8085
Communications
Analog Communication Systems Digital Communication Systems Random Signals and Noise Fundamentals of Information Theory Noise In Digital Communication
Electromagnetics
Waveguides Antennas Miscellaneous Transmission Lines Maxwell Equations Uniform Plane Waves
EXAM MAP
Joint Entrance Examination
JEE MainJEE AdvancedWB JEEBITSATMHT CETKCETCOMEDKVITEEEAP EAPCET
Medical
NEETAIIMS
Graduate Aptitude Test in Engineering
GATE CSEGATE ECEGATE EEGATE MEGATE CEGATE PIGATE IN
Civil Services
UPSC Civil Service
Defence
NDA
Staff Selection Commission
SSC CGL Tier I
CBSE
Class 12