1
GATE ECE 2009
MCQ (Single Correct Answer)
+2
-0.6
The Nyquist plot of a stable transfer function G(s) is shown in the figure. We are interested in the stability of the closed loop system in the feedback configuration shown.
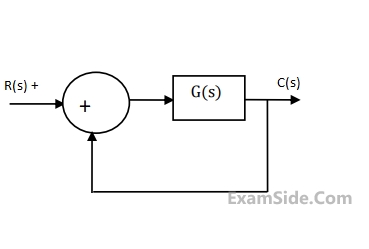
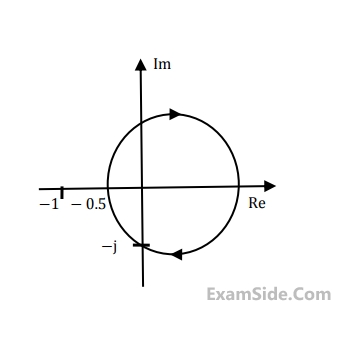 Which of the foloowing statements is true?
Which of the foloowing statements is true?

 Which of the foloowing statements is true?
Which of the foloowing statements is true?
2
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The impulse response h(t) of a linear time invariant system is given by h(t) = $${e^{ - 2t}}u(t),$$ where u(t) denotes the unit step function.
The output of this system to the sinusoidal input x(t) = 2cos(t) for all time 't' is
3
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The magnitude of frequency response of an underdamped second order system is 5 at 0 rad/sec and peaks to $${{10} \over {\sqrt 3 }}$$ at 5 $$\sqrt 2 $$ rad/sec. The transfer function of the system is
4
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The impulse response h(t) of a linear time invariant system is given by h(t) = $${e^{ - 2t}}u(t),$$ where u(t) denotes the unit step function.
The frequency response H(ω) of the system in terms of angular frequency 'ω' is given by h( ω)
Questions Asked from Frequency Response Analysis (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2023 (1)
GATE ECE 2018 (2)
GATE ECE 2017 Set 1 (1)
GATE ECE 2017 Set 2 (1)
GATE ECE 2016 Set 2 (2)
GATE ECE 2015 Set 2 (1)
GATE ECE 2014 Set 2 (1)
GATE ECE 2014 Set 1 (1)
GATE ECE 2011 (2)
GATE ECE 2009 (2)
GATE ECE 2008 (3)
GATE ECE 2007 (1)
GATE ECE 2006 (4)
GATE ECE 2005 (3)
GATE ECE 2004 (2)
GATE ECE 2003 (2)
GATE ECE 2002 (1)
GATE ECE 2001 (1)
GATE ECE 1992 (1)
GATE ECE 1991 (1)
GATE ECE 1989 (1)
GATE ECE 1987 (2)
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics