A coin has probability $$p$$ of showing head when tossed. It is tossed $$n$$ times. Let $${p_n}$$ denote the probability that no two (or more) consecutive heads occur. Prove that $${p_1} = 1,{p_2} = 1 - {p^2}$$ and $${p_n} = \left( {1 - p} \right).\,\,{p_{n - 1}} + p\left( {1 - p} \right){p_{n - 2}}$$ for all $$n \ge 3.$$

Eight players $${P_1},{P_2},.....{P_8}$$ play a knock-out tournament. It is known that whenever the players $${P_i}$$ and $${P_j}$$ play, the player $${P_i}$$ will win if $$i < j.$$ Assuming that the players are paired at random in each round, what is the probability that the player $${P_4}$$ reaches the final?

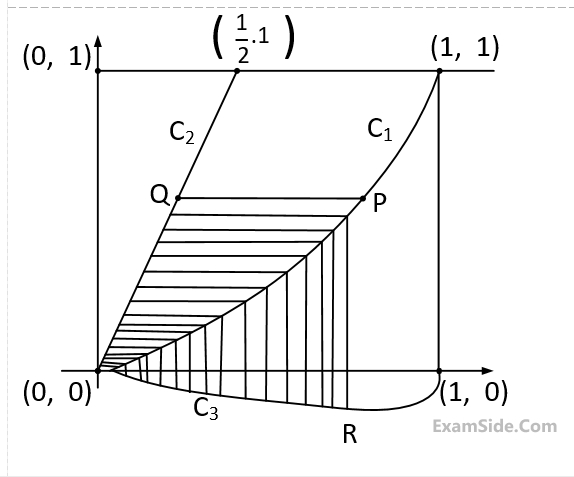
Let $${C_1}$$ and $${C_2}$$ be the graphs of the functions $$y = {x^2}$$ and $$y = 2x,$$ $$0 \le x \le 1$$ respectively. Let $${C_3}$$ be the graph of a function $$y=f(x),$$ $$0 \le x \le 1,$$ $$f(0)=0.$$ For a point $$P$$ on $${C_1},$$ let the lines through $$P,$$ parallel to the axes, meet $${C_2}$$ and $${C_3}$$ at $$Q$$ and $$R$$ respectively (see figure.) If for every position of $$P$$ (on $${C_1}$$ ), the areas of the shaded regions $$OPQ$$ and $$ORP$$ are equal, determine the function$$f(x).$$

Three players, $$A,B$$ and $$C,$$ toss a coin cyclically in that order (that is $$A, B, C, A, B, C, A, B,...$$) till a head shows. Let $$p$$ be the probability that the coin shows a head. Let $$\alpha ,\,\,\,\beta $$ and $$\gamma $$ be, respectively, the probabilities that $$A, B$$ and $$C$$ gets the first head. Prove that $$\beta = \left( {1 - p} \right)\alpha $$ Determine $$\alpha ,\beta $$ and $$\gamma $$ (in terms of $$p$$).