The electric field of a uniform plane wave travelling along the negative $$z$$ direction is given by the following equation: $$$\overrightarrow E {}_w^i = \left( {{{\widehat a}_{_x}} + j{{\widehat a}_{_y}}} \right){E_0}{e^{jkz}}$$$

This wave is incident upon a receiving antenna placed at the origin and whose radiated electric field towards the incident wave is given by the following equation:

$$${\overrightarrow E _{_a}} = \left( {{{\widehat a}_{_x}} + 2{{\widehat a}_{_y}}} \right){E_1}{1 \over r}{e^{ - jkr}}$$$

The polarization of the incident wave, the polarization of the antenna and losses due to the polarization mismatch are, respectively,

The electric field intensity of a plane wave propagating in a lossless non-magnetic medium is given by the following expression
$$\overrightarrow E \left( {z,t} \right) = {\widehat a_x}5\cos \left( {2\pi \times {{10}^9}t + \beta z} \right)$$ $$$ + {\widehat a_y}3\cos \left( {2\pi \times {{10}^9}t + \beta z - {\pi \over 2}} \right)$$$

The type of the polarization is

Consider a uniform plane wave with amplitude $$\left( {{E_0}} \right)$$ of $$10\,\,\,V/m$$ and $$1.1 GHz$$ frequency travelling in air, and incident normally on a dielectric medium with complex relative permittivity $$\left( {{\varepsilon _r}} \right)$$ and permeability $$\left( {{\mu _r}} \right)$$ as shown in the figure.

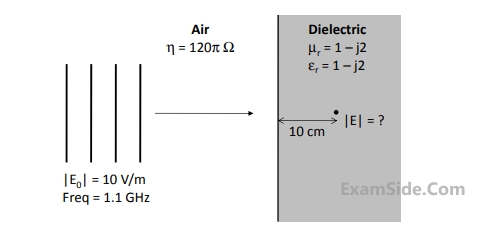
The magnitude of the transmitted electric field component (in V/m) after it has travelled a distance of $$10$$ cm inside the dielectric region is ________.

The electric field intensity of a plane wave traveling in free space is given by the following expression

$$E\left( {x,t} \right) = {\widehat a_{_y}}24\pi \,\,\cos \left( {\omega t - {k_0}x} \right)\,\,\,\left( {V/m} \right)$$. In this field, consider a square area $$10 cm$$ $$ \times $$ $$10 cm$$ on a plane $$x + y = 1$$. The total time-averaged power $$(in mW)$$ passing through the square area is ________.