GATE ECE 2013 | Uniform Plane Waves Question 21 | Electromagnetics

GATE ECE 2013

MCQ (Single Correct Answer)

-0.6

A monochromatic plane wave of wavelength $$\lambda = 600$$ is propagating in the direction as shown in the figure below. $${\overrightarrow E _i},\,{\overrightarrow E _r}$$ and $${\overrightarrow E _t}$$ denote incident, reflected, and transmitted electric field vectors associated with the wave. GATE ECE 2013 Electromagnetics - Uniform Plane Waves Question 27 English

GATE ECE 2013 Electromagnetics - Uniform Plane Waves Question 27 English

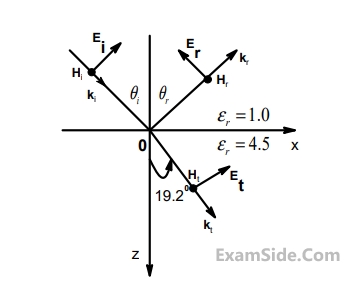
The expression for $${\overrightarrow E _r}$$ is

$$0.23{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}\left( {x - z} \right)} \over {3\sqrt 2 }}}}\,\,\,V/m$$

$$ - {{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}z} \over 3}}}\,\,\,V/m$$

$$0.44{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}\left( {x - z} \right)} \over {3\sqrt 2 }}}}\,\,\,V/m$$

$${{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}\left( {x + z} \right)} \over 3}}}\,\,V/m$$

GATE ECE 2013

MCQ (Single Correct Answer)

-0.6

GATE ECE 2013 Electromagnetics - Uniform Plane Waves Question 28 English

The angle of incidence $${\theta _i}$$ and the expression for $${\overrightarrow E _i}$$ are

$${60^ \circ }\,\,\,and\,\,{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}\left( {x + z} \right)} \over {3\sqrt 2 }}}}\,\,V/m$$

$${45^ \circ }\,\,\,and\,\,{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}z} \over 3}}}\,\,V/m$$

$${45^ \circ }\,\,\,and\,\,{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}\left( {x + z} \right)} \over {3\sqrt 2 }}}}\,\,V/m$$

$${60^ \circ }\,\,\,and\,\,{{{E_0}} \over {\sqrt 2 }}\left( {{{\widehat a}_x} - {{\widehat a}_z}} \right){e^{ - j{{\pi \times {{10}^4}z} \over 3}}}\,\,V/m$$

GATE ECE 2011

MCQ (Single Correct Answer)

-0.6

The electric and magnetic fields for a TEM wave of frequency $$14 GHz$$ in a homogeneous medium of relative permittivity $${\varepsilon _r}$$ and relative permeability $${\mu _r} = 1$$ are given by $$$\overrightarrow E = {E_p}\,\,{e^{j\left( {\omega t - 280\pi y} \right)}}\,\,{\widehat u_z}\,\,V/m$$$ $$$\overrightarrow H = \,\,3\,\,{e^{j\left( {\omega \,t - 280\,\,\pi \,y} \right)}}\,\,\widehat u{\,_x}\,\,A/m$$$

Assuming the speed of light in free space to be $$3\,\, \times {10^8}\,\,\,m/s,$$ the intrinsic impedance of free space to be $$120\,\,\,\pi $$, the relative permittivity $${\varepsilon _r}$$ of the medium and the electric field amplitude $${E_p}$$ are

$${\varepsilon _r} = 3,\,\,{E_p} = 120\,\pi $$

$${\varepsilon _r} = 3,\,\,{E_p} = 360\,\pi $$

$${\varepsilon _r} = 9,\,\,{E_p} = 360\,\pi $$

$${\varepsilon _r} = 9,\,\,{E_p} = 120\,\pi $$

GATE ECE 2010

MCQ (Single Correct Answer)

-0.6

A plane wave having the electric field component $$${\overrightarrow E _i} = 24\,\,\cos \,\,\left( {3 \times {{10}^8}\,t - \beta \,y} \right){\widehat a_z}\,\,V/m$$$
and traveling in free space is incident normally on a lossless medium with $$\mu = {\mu _0}$$ and $$\varepsilon = 9\,\,{\varepsilon _0},$$ which occupies the region $$y \ge 0.$$ The reflected magnetic field component is given by

$${1 \over {10{\mkern 1mu} \pi }}\cos {\mkern 1mu} {\mkern 1mu} \left( {3 \times {{10}^8}{\mkern 1mu} t - y} \right)\hat a{\,_x}{\mkern 1mu} {\mkern 1mu} A/m$$

$${1 \over {20{\mkern 1mu} \pi }}\cos {\mkern 1mu} {\mkern 1mu} \left( {3 \times {{10}^8}{\mkern 1mu} t - y} \right)\hat a{\,_x}{\mkern 1mu} {\mkern 1mu} A/m$$

$$ - {1 \over {20{\mkern 1mu} \pi }}\cos {\mkern 1mu} {\mkern 1mu} \left( {3 \times {{10}^8}{\mkern 1mu} t - y} \right)\hat a{\,_x}{\mkern 1mu} {\mkern 1mu} A/m$$

$$ - {1 \over {10{\mkern 1mu} \pi }}\cos {\mkern 1mu} {\mkern 1mu} \left( {3 \times {{10}^8}{\mkern 1mu} t - y} \right)\hat a{\,_x}{\mkern 1mu} {\mkern 1mu} A/m$$

PREVIOUS NEXT