A medium has breakdown strength of $$16$$ KV/m r.m.s. Its relative permeability is $$1.0$$ and relative permittivity is $$4.0$$. A plane electromagnetic wave is transmitted through the medium. Calculate the maximum possible power flow density and the associated magnetic filed.

A plane wave in free space with
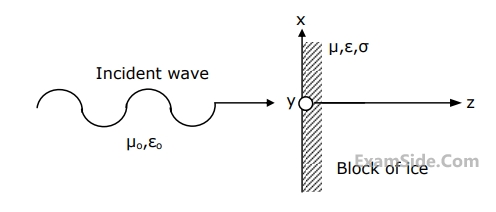
$$\overrightarrow E = \left( {\sqrt \pi } \right)\left( {10.0\,\widehat x + 11.8\,\widehat y} \right)\exp \left[ {j\left( {4\pi \times {{10}^8}\,t - k\,z} \right)} \right]$$
where $$\widehat x$$ and $$\widehat y$$ are unit vectors in the $$x$$- and $$y$$-directions respectively is incident normally on a semi-infinite block of ice as shown in Fig. For ice, $$\mu = {\mu _0},\,\,\,\sigma = 0$$ and $$\varepsilon = 9{\varepsilon _0}\left( {1 - j0.001} \right)$$.

(a) Calculate the average power density associated with the incident wave.

(b) Calculate the skin depth in ice.

(c) Estimate the average power density at a distance of 5 times the skins depth in the ice block, measured from the interface.

A plane wave with $$\overrightarrow E = 10\,{e^{j\left( {\omega t - \beta z} \right)\,}}\,\,{\overrightarrow a _{_y}}$$ is incident normally on a thick plane conductor lying in the $$X - Y$$ plane. Its conductivity is $$6 \times {10^6}\,\,\,S/m\,\,\,$$ and surface impedance is $$5 \times {0^{ - 4}}\,\angle {45^0}\Omega $$. Determine the propagation constant and the skin depth in the conductor.

The electric field vector of a wave is given as $$$\vec E = {E_0}{\mkern 1mu} {e^{j\left( {\omega t + 3x - 4y} \right)}}{\mkern 1mu} {{8{{\vec a}_x} + 6{{\vec a}_y} + 5{{\vec a}_z}} \over {\sqrt {125} }}\,\,V/m$$$

Its frequency is 10 GHz.

(i) Investigate if this wave is a plane wave.
(ii) Determine its propagation constant, and
(iii) Calculate the phase velocity in $$y$$-direction.