1
GATE ECE 2014 Set 1
Numerical
+2
-0
In spherical coordinates, let $${{{\widehat a}_{_0}},\,{{\widehat a}_{_\phi }}}$$ denote unit vectors along the $$\theta ,\,\,\phi $$directions.
$$$E = {{100} \over r}\sin \,\theta \cos \left( {\omega t - \beta r} \right){\widehat a_{_\theta }}\,\,V/m$$$
and $$$H = {{0.265} \over r}\sin \,\theta \cos \left( {\omega t - \beta r} \right){\widehat a_{_\phi }}\,\,A/m$$$
and $$$H = {{0.265} \over r}\sin \,\theta \cos \left( {\omega t - \beta r} \right){\widehat a_{_\phi }}\,\,A/m$$$
Represent the electric and magnetic field components of the EM wave at large distances $$r$$ from a dipole antenna, in free space. The average power $$(W)$$ crossing the hemispherical shell located at $$r = 1\,\,km$$, $$0 \le \theta \le \pi /2$$ _______.
Your input ____
2
GATE ECE 2014 Set 3
Numerical
+2
-0
Assume that a plane wave in air with an electric field
$$\overrightarrow E = 10\cos \left( {\omega t - 3x - \sqrt {3z} } \right){\widehat a_{_y}}\,\,\,V/m$$ is incident
on a non-magnetic dielectric slab of relative permittivity $$3$$ which covers the region $$z > 0$$ . The angle of transmission in the dielectric slab is _______ degrees.
$$\overrightarrow E = 10\cos \left( {\omega t - 3x - \sqrt {3z} } \right){\widehat a_{_y}}\,\,\,V/m$$ is incident
on a non-magnetic dielectric slab of relative permittivity $$3$$ which covers the region $$z > 0$$ . The angle of transmission in the dielectric slab is _______ degrees.
Your input ____
3
GATE ECE 2014 Set 3
MCQ (Single Correct Answer)
+2
-0.6
A region shown below contains a perfect conducting half-space and air. The surface current $${\overrightarrow K _{_s}}$$ on the surface of the perfect conductor is $${\overrightarrow K _{_s}} = \widehat x\,2$$ amperes per meter. The tangential $$\overrightarrow H $$ field in the air just above the perfect conductor is
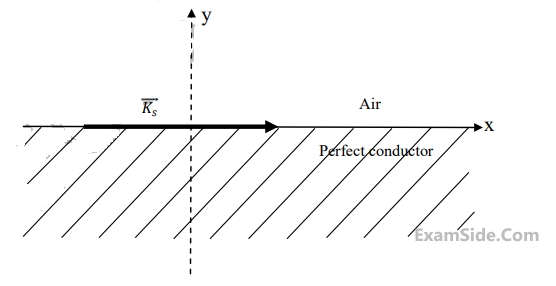

4
GATE ECE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
If the electric field of a plane wave is
$$$\overrightarrow E \left( {z,t} \right) = \widehat x3\cos \left( {\omega t - kz + {{30}^ \circ }} \right) - \widehat y4\sin \left( {\omega t - kz + {{45}^ \circ }} \right)\left( {mV/m} \right)$$$
The polarization state of the plane wave is
Questions Asked from Uniform Plane Waves (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2024 (1)
GATE ECE 2023 (2)
GATE ECE 2017 Set 1 (1)
GATE ECE 2016 Set 1 (1)
GATE ECE 2015 Set 2 (1)
GATE ECE 2015 Set 1 (2)
GATE ECE 2014 Set 1 (1)
GATE ECE 2014 Set 3 (2)
GATE ECE 2014 Set 2 (1)
GATE ECE 2013 (2)
GATE ECE 2011 (1)
GATE ECE 2010 (1)
GATE ECE 2008 (1)
GATE ECE 2007 (1)
GATE ECE 2006 (3)
GATE ECE 2004 (1)
GATE ECE 2003 (3)
GATE ECE 2002 (2)
GATE ECE 2001 (1)
GATE ECE 2000 (1)
GATE ECE 1996 (2)
GATE ECE 1993 (2)
GATE ECE 1991 (1)
GATE ECE 1989 (1)
GATE ECE 1988 (1)
GATE ECE 1987 (1)
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics