A random variable X, distributed normally as N(0, 1), undergoes the transformation Y = h(X), given in the figure. The form of the probability density function of Y is

(In the options given below, a, b, c are non-zero constants and g(y) is piece-wise continuous function)

Let X(t) be a white Gaussian noise with power spectral density $$\frac{1}{2}$$W/Hz. If X(t) is input to an LTI system with impulse response $$e^{-t}u(t)$$. The average power of the system output is ____________ W (rounded off to two decimal places).

Consider a real valued source whose samples are independent and identically distributed random variables with the probability density function, f(x), as shown in the figure.

Consider a 1 bit quantizer that maps positive samples to value $$\alpha$$ and others to value $$\beta$$. If $$\alpha$$* and $$\beta$$* are the respective choices for $$\alpha$$ and $$\beta$$ that minimize the mean square quantization error, then ($$\alpha$$* $$-$$ $$\beta$$*) = ___________ (rounded off to two decimal places).

As shown in Figure (b). The output of the low pass filter is $$y(t)$$.

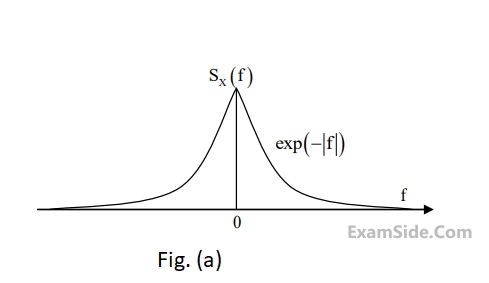
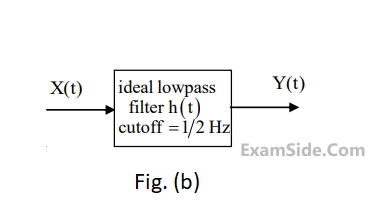
Let $$E$$ be the expectation operator and consider the following statements :
$$\left( {\rm I} \right)$$ $$E\left( {X\left( t \right)} \right) = E\left( {Y\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}} \right)$$ $$\,\,\,\,\,\,\,\,E\left( {{X^2}\left( t \right)} \right) = E\left( {{Y^2}\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}{\rm I}} \right)\,$$ $$\,\,\,\,\,\,E\left( {{Y^2}\left( t \right)} \right) = 2$$

Select the correct option: