Let $$X(t)$$ be a wide sense stationary random process with the power spectral density $${S_x}\left( f \right)$$ as shown in figure (a), where $$f$$ is in Hertz $$(Hz)$$. The random process $$X(t)$$ is input to an ideal low pass filter with the frequency response $$$H\left( f \right) = \left\{ {\matrix{ {1,} & {\left| f \right| \le {1 \over 2}Hz} \cr {0,} & {\left| f \right| > {1 \over 2}Hz} \cr } } \right.$$$

As shown in Figure (b). The output of the low pass filter is $$y(t)$$.

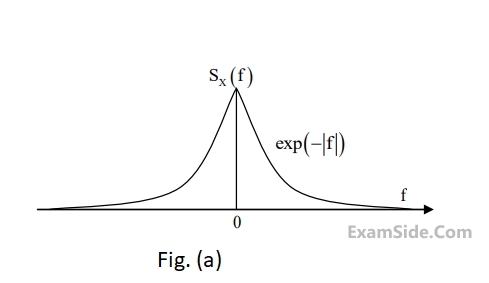
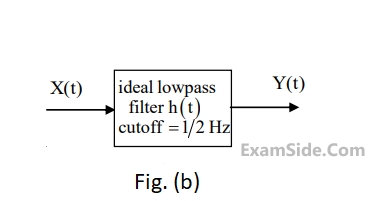
Let $$E$$ be the expectation operator and consider the following statements :
$$\left( {\rm I} \right)$$ $$E\left( {X\left( t \right)} \right) = E\left( {Y\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}} \right)$$ $$\,\,\,\,\,\,\,\,E\left( {{X^2}\left( t \right)} \right) = E\left( {{Y^2}\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}{\rm I}} \right)\,$$ $$\,\,\,\,\,\,E\left( {{Y^2}\left( t \right)} \right) = 2$$

Select the correct option:

A wide sense stationary random process $$X(t)$$ passes through the $$LTI$$ system shown in the figure. If the autocorrelation function of $$X(t)$$ is $${R_x}\left( \tau \right),$$ then the autocorrelation function $${R_x}\left( \tau \right),$$ of the output $$Y(t)$$ is equal to

An information source generates a binary sequence $$\left\{ {{\alpha _n}} \right\}.{\alpha _n}$$ can take one of the two possible values −1 and +1 with equal probability and are statistically independent and identically distributed. This sequence is pre-coded to obtain another sequence $$\left\{ {{\beta _n}} \right\},$$ as $${\beta _n} = {\alpha _n} + k{\mkern 1mu} {\alpha _{n - 3}}$$ . The sequence $$\left\{ {{\beta _n}} \right\}$$ is used to modulate a pulse $$g(t)$$ to generate the baseband signal

$$x\left( t \right) = \sum\limits_{n = - \infty }^\infty {{\beta _n}g\left( {t - nT} \right),} $$ where $$g\left( t \right) = \left\{ {\matrix{ {1,} & {0 \le t \le T} \cr 0 & {otherwise} \cr } } \right.$$

If there is a null at $$f = {1 \over {3T}}$$ in the power spectral density of $$X(t)$$, then $$k$$ is _________.

Consider random process $$X(t) = 3V(t) - 8$$, where $$V$$ $$(t)$$ is a zero mean stationary random process with autocorrelation $${R_v}\left( \tau \right) = 4{e^{ - 5\left| \tau \right|}}$$. The power of $$X(t)$$ is _______.