Bits 1 and 0 are transmitted with equal probability. At the receiver, the pdf of the respective received signals for both bits are as shown below.

The optimum threshold to achieve minimum bit error rate (BER) is

X(t) is a stationary random process with autocorrelation function R_x$$\left( \tau \right)$$= exp$$\left( { - \pi {\tau ^2}} \right)$$. This process is passed through the system shown below. The power spectral density of the output process Y(t) is

X(t) is a stationary process with the power spectral density S_x(f) > 0 for all f. The process is passed through a system shown below.

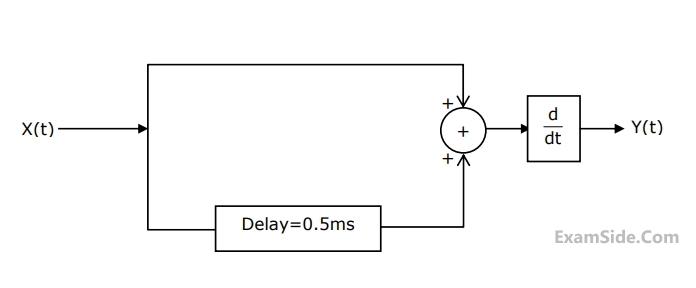
Let S_y(f) be the power spectral density of Y(t). Which one of the following statements is correct?

Noise with double-sided power spectral density of K over all frequencies is passed through a RC low pass filter with 3-dB cut-off frequency of f_c. The noise power at the filter output is