
One mole of a monatomic ideal gas undergoes the cyclic process $\mathrm{J} \rightarrow \mathrm{K} \rightarrow \mathrm{L} \rightarrow \mathrm{M} \rightarrow \mathrm{J}$, as shown in the P-T diagram.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
[ $\mathcal{R}$ is the gas constant.]
| List-I | List-II |
|---|---|
| (P) Work done in the complete cyclic process | (1) $RT_0 - 4RT_0 \ln 2$ |
| (Q) Change in the internal energy of the gas in the process JK | (2) $0$ |
| (R) Heat given to the gas in the process KL | (3) $3RT_0$ |
| (S) Change in the internal energy of the gas in the process MJ | (4) $-2RT_0 \ln 2$ |
| (5) $-3RT_0 \ln 2$ |

Four identical thin, square metal sheets, $S_1, S_2, S_3$ and $S_4$, each of side $a$ are kept parallel to each other with equal distance $d(\ll a)$ between them, as shown in the figure. Let $${C_0} = {{{\varepsilon _0}{a^2}} \over d}$$, where $\varepsilon_0$ is the permittivity of free space.
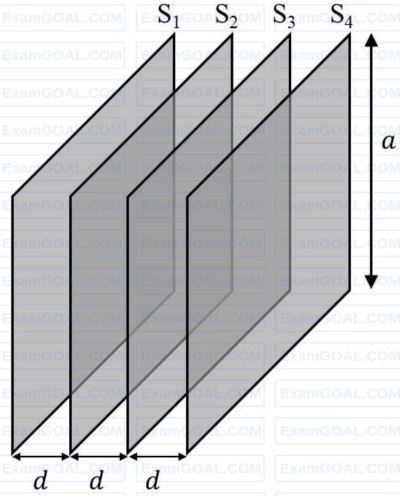
Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) The capacitance between $S_1$ and $S_4$, with $S_2$ and $S_3$ not connected, is | (1) $3C_0$ |
| (Q) The capacitance between $S_1$ and $S_4$, with $S_2$ shorted to $S_3$, is | (2) $\frac{C_0}{2}$ |
| (R) The capacitance between $S_1$ and $S_3$, with $S_2$ shorted to $S_4$, is | (3) $\frac{C_0}{3}$ |
| (S) The capacitance between $S_1$ and $S_2$, with $S_3$ shorted to $S_1$, and $S_2$ shorted to $S_4$, is | (4) $\frac{2C_0}{3}$ |
| (5) $2C_0$ |

A light ray is incident on the surface of a sphere of refractive index $n$ at an angle of incidence $\theta_0$. The ray partially refracts into the sphere with angle of refraction $\phi_0$ and then partly reflects from the back surface. The reflected ray then emerges out of the sphere after a partial refraction. The total angle of deviation of the emergent ray with respect to the incident ray is $\alpha$. Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) If $n = 2$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (1) $30^\circ$ and $0^\circ$ |
| (Q) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (2) $60^\circ$ and $0^\circ$ |
| (R) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\phi_0$ will be | (3) $45^\circ$ and $0^\circ$ |
| (S) If $n = \sqrt{2}$ and $\theta_0 = 45^\circ$, then all the possible values of $\alpha$ will be | (4) $150^\circ$ |
| (5) $0^\circ$ |

The circuit shown in the figure contains an inductor $L$, a capacitor $C_0$, a resistor $R_0$ and an ideal battery. The circuit also contains two keys $\mathrm{K}_1$ and $\mathrm{K}_2$. Initially, both the keys are open and there is no charge on the capacitor. At an instant, key $\mathrm{K}_1$ is closed and immediately after this the current in $R_0$ is found to be $I_1$. After a long time, the current attains a steady state value $I_2$. Thereafter, $\mathrm{K}_2$ is closed and simultaneously $\mathrm{K}_1$ is opened and the voltage across $C_0$ oscillates with amplitude $V_0$ and angular frequency $\omega_0$.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) The value of $I_1$ in Ampere is | (1) $0$ |
| (Q) The value of $I_2$ in Ampere is | (2) $2$ |
| (R) The value of $\omega_0$ in kilo-radians/s is | (3) $4$ |
| (S) The value of $V_0$ in Volt is | (4) $20$ |
| (5) $200$ |