In the following reaction sequence, the major product $\mathbf{Q}$ is

The species formed on fluorination of phosphorus pentachloride in a polar organic solvent are

An aqueous solution of hydrazine $\left(\mathrm{N}_2 \mathrm{H}_4\right)$ is electrochemically oxidized by $\mathrm{O}_2$, thereby releasing chemical energy in the form of electrical energy. One of the products generated from the electrochemical reaction is $\mathrm{N}_2(\mathrm{~g})$.

Choose the correct statement(s) about the above process

The option(s) with correct sequence of reagents for the conversion of $\mathbf{P}$ to $\mathbf{Q}$ is(are)

To form a complete monolayer of acetic acid on $1 \mathrm{~g}$ of charcoal, $100 \mathrm{~mL}$ of $0.5 \mathrm{M}$ acetic acid was used. Some of the acetic acid remained unadsorbed. To neutralize the unadsorbed acetic acid, 40 $\mathrm{mL}$ of $1 \mathrm{M} \mathrm{NaOH}$ solution was required. If each molecule of acetic acid occupies $\mathbf{P} \times 10^{-23} \mathrm{~m}^2$ surface area on charcoal, the value of $\mathbf{P}$ is _____.

[Use given data: Surface area of charcoal $=1.5 \times 10^2 \mathrm{~m}^2 \mathrm{~g}^{-1}$; Avogadro's number $\left(\mathrm{N}_{\mathrm{A}}\right)=6.0 \times 10^{23}$ $\left.\mathrm{mol}^{-1}\right]$

For a double strand DNA, one strand is given below:

The amount of energy required to split the double strand DNA into two single strands is _______ kcal $\operatorname{mol}^{-1}$.

[Given: Average energy per H-bond for A-T base pair $=1.0 ~\mathrm{kcal}~ \mathrm{mol}^{-1}$, G-C base pair $=1.5 ~\mathrm{kcal}$ $\mathrm{mol}^{-1}$, and A-U base pair $=1.25 ~\mathrm{kcal} ~\mathrm{mol}^{-1}$. Ignore electrostatic repulsion between the phosphate groups.]

A sample initially contains only U-238 isotope of uranium. With time, some of the U-238 radioactively decays into $\mathrm{Pb}-206$ while the rest of it remains undisintegrated.

When the age of the sample is $\mathbf{P} \times 10^8$ years, the ratio of mass of $\mathrm{Pb}-206$ to that of $\mathrm{U}-238$ in the sample is found to be 7. The value of $\mathbf{P}$ is _______.

[Given: Half-life of $\mathrm{U}-238$ is $4.5 \times 10^9$ years; $\log _e 2=0.693$ ]

An organic compound $\mathbf{P}$ having molecular formula $\mathrm{C}_6 \mathrm{H}_6 \mathrm{O}_3$ gives ferric chloride test and does not have intramolecular hydrogen bond. The compound $\mathbf{P}$ reacts with 3 equivalents of $\mathrm{NH}_2 \mathrm{OH}$ to produce oxime $\mathbf{Q}$. Treatment of $\mathbf{P}$ with excess methyl iodide in the presence of $\mathrm{KOH}$ produces compound $\mathbf{R}$ as the major product. Reaction of $\mathbf{R}$ with excess iso-butylmagnesium bromide followed by treatment with $\mathrm{H}_3 \mathrm{O}^{+}$gives compound $\mathbf{S}$ as the major product.

The total number of methyl $\left(-\mathrm{CH}_3\right)$ group(s) in compound $\mathbf{S}$ is ___.

Considering only the principal values of the inverse trigonometric functions, the value of

$$ \tan \left(\sin ^{-1}\left(\frac{3}{5}\right)-2 \cos ^{-1}\left(\frac{2}{\sqrt{5}}\right)\right) $$

is

Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function defined by

$$ f(x)=\left\{\begin{array}{cc} x^2 \sin \left(\frac{\pi}{x^2}\right), & \text { if } x \neq 0, \\ 0, & \text { if } x=0 . \end{array}\right. $$

Then which of the following statements is TRUE?

Let $S$ be the set of all $(\alpha, \beta) \in \mathbb{R} \times \mathbb{R}$ such that

$$ \lim\limits_{x \rightarrow \infty} \frac{\sin \left(x^2\right)\left(\log _e x\right)^\alpha \sin \left(\frac{1}{x^2}\right)}{x^{\alpha \beta}\left(\log _e(1+x)\right)^\beta}=0 . $$

Then which of the following is (are) correct?

Let the function $f: \mathbb{R} \rightarrow \mathbb{R}$ be defined by

$$ f(x)=\frac{\sin x}{e^{\pi x}} \frac{\left(x^{2023}+2024 x+2025\right)}{\left(x^2-x+3\right)}+\frac{2}{e^{\pi x}} \frac{\left(x^{2023}+2024 x+2025\right)}{\left(x^2-x+3\right)} . $$

Then the number of solutions of $f(x)=0$ in $\mathbb{R}$ is _________.

Let $\vec{p}=2 \hat{i}+\hat{j}+3 \hat{k}$ and $\vec{q}=\hat{i}-\hat{j}+\hat{k}$. If for some real numbers $\alpha, \beta$, and $\gamma$, we have

$$ 15 \hat{i}+10 \hat{j}+6 \hat{k}=\alpha(2 \vec{p}+\vec{q})+\beta(\vec{p}-2 \vec{q})+\gamma(\vec{p} \times \vec{q}), $$

then the value of $\gamma$ is ________.

Let the function $f:[1, \infty) \rightarrow \mathbb{R}$ be defined by

$$ f(t)=\left\{\begin{array}{cc} (-1)^{n+1} 2, & \text { if } t=2 n-1, n \in \mathbb{N}, \\ \frac{(2 n+1-t)}{2} f(2 n-1)+\frac{(t-(2 n-1))}{2} f(2 n+1), & \text { if } 2 n-1 < t < 2 n+1, n \in \mathbb{N} . \end{array}\right. $$

Define $g(x)=\int_1^x f(t) d t, x \in(1, \infty)$. Let $\alpha$ denote the number of solutions of the equation $g(x)=0$ in the interval $(1,8]$ and $\beta=\lim \limits_{x \rightarrow l+} \frac{g(x)}{x-1}$.

Then the value of $\alpha+\beta$ is equal to _______.

A region in the form of an equilateral triangle (in $x-y$ plane) of height $L$ has a uniform magnetic field $\vec{B}$ pointing in the $+z$-direction. A conducting loop $\mathrm{PQR}$, in the form of an equilateral triangle of the same height $L$, is placed in the $x-y$ plane with its vertex $\mathrm{P}$ at $x=0$ in the orientation shown in the figure. At $t=0$, the loop starts entering the region of the magnetic field with a uniform velocity $\vec{v}$ along the $+x$-direction. The plane of the loop and its orientation remain unchanged throughout its motion.

Which of the following graph best depicts the variation of the induced emf $(E)$ in the loop as a function of the distance $(x)$ starting from $x=0$ ?

A particle of mass $m$ is under the influence of the gravitational field of a body of mass $M(\gg m)$. The particle is moving in a circular orbit of radius $r_0$ with time period $T_0$ around the mass $M$. Then, the particle is subjected to an additional central force, corresponding to the potential energy $V_{\mathrm{c}}(r)=m \alpha / r^3$, where $\alpha$ is a positive constant of suitable dimensions and $r$ is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius $r_0$ in the combined gravitational potential due to $M$ and $V_{\mathrm{c}}(r)$, but with a new time period $T_1$, then $\left(T_1^2-T_0^2\right) / T_1^2$ is given by

[G is the gravitational constant.]

A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass $m$ and radius $r$ and it is in a uniform vertical magnetic field $B_0$, as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity $g$, on two conducting supports at $\mathrm{P}$ and $\mathrm{Q}$. When a current $I$ is passed through the loop, the loop turns about the line $\mathrm{PQ}$ by an angle $\theta$ given by

A small electric dipole $\vec{p}_0$, having a moment of inertia $I$ about its center, is kept at a distance $r$ from the center of a spherical shell of radius $R$. The surface charge density $\sigma$ is uniformly distributed on the spherical shell. The dipole is initially oriented at a small angle $\theta$ as shown in the figure. While staying at a distance $r$, the dipole is free to rotate about its center.

If released from rest, then which of the following statement(s) is(are) correct?

[ $\varepsilon_0$ is the permittivity of free space.]

A table tennis ball has radius $(3 / 2) \times 10^{-2} \mathrm{~m}$ and mass $(22 / 7) \times 10^{-3} \mathrm{~kg}$. It is slowly pushed down into a swimming pool to a depth of $d=0.7 \mathrm{~m}$ below the water surface and then released from rest. It emerges from the water surface at speed $v$, without getting wet, and rises up to a height $H$. Which of the following option(s) is(are) correct?

[Given: $\pi=22 / 7, g=10 \mathrm{~m} \mathrm{~s}^{-2}$, density of water $=1 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$, viscosity of water $=1 \times 10^{-3} \mathrm{~Pa}$-s.]

A positive, singly ionized atom of mass number $A_{\mathrm{M}}$ is accelerated from rest by the voltage $192 \mathrm{~V}$. Thereafter, it enters a rectangular region of width $w$ with magnetic field $\vec{B}_0=0.1 \hat{k}$ Tesla, as shown in the figure. The ion finally hits a detector at the distance $x$ below its starting trajectory.

[Given: Mass of neutron/proton $=(5 / 3) \times 10^{-27} \mathrm{~kg}$, charge of the electron $=1.6 \times 10^{-19} \mathrm{C}$.]

Which of the following option(s) is(are) correct?

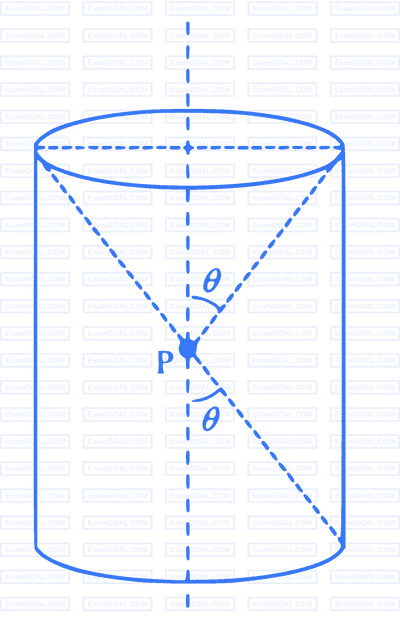
A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.

Two equilateral-triangular prisms $\mathrm{P}_1$ and $\mathrm{P}_2$ are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism $\mathrm{P}_1$ at an angle of incidence $\theta$ such that the outgoing ray undergoes minimum deviation in prism $\mathrm{P}_2$. If the respective refractive indices of $\mathrm{P}_1$ and $\mathrm{P}_2$ are $\sqrt{\frac{3}{2}}$ and $\sqrt{3}$, then $\theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \left(\frac{\pi}{\beta}\right)\right]$, where the value of $\beta$ is ____.

An infinitely long thin wire, having a uniform charge density per unit length of $5 \mathrm{nC} / \mathrm{m}$, is passing through a spherical shell of radius $1 \mathrm{~m}$, as shown in the figure. A $10 \mathrm{nC}$ charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points $\mathrm{P}$ and $\mathrm{R}$, in Volt, is ________.

[Given: In SI units $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$. Ignore the area pierced by the wire.]