IIT-JEE 2004 Screening
Paper was held on
Sun, Apr 11, 2004 9:00 AM
Chemistry
1
The radius of which of the following orbit is same as that of the first Bohr's orbit of hydrogen atom?
2
The pair of compounds having metals in their highest oxidation state is
3
According to molecular orbital theory which of the following statement about the magnetic character and bond order is correct regarding $$O_2^+$$
4
A sodium salt on treatment with MgCl3 gives white precipitate only on heating. The anion of the sodium salt is
Mathematics
1
The area enclosed between the curves $$y = a{x^2}$$ and
$$x = a{y^2}\left( {a > 0} \right)$$ is $$1$$ sq. unit, then the value of $$a$$ is
$$x = a{y^2}\left( {a > 0} \right)$$ is $$1$$ sq. unit, then the value of $$a$$ is
2
If $$f(x)$$ is differentiable and $$\int\limits_0^{{t^2}} {xf\left( x \right)dx = {2 \over 5}{t^5},} $$ then $$f\left( {{4 \over {25}}} \right)$$ equals
3
If $$y=y(x)$$ and $${{2 + \sin x} \over {y + 1}}\left( {{{dy} \over {dx}}} \right) = - \cos x,y\left( 0 \right) = 1,$$
then $$y\left( {{\pi \over 2}} \right)$$ equals
then $$y\left( {{\pi \over 2}} \right)$$ equals
4
If three distinct numbers are chosen randomly from the first $$100$$ natural numbers, then the probability that all three of them are divisible by both $$2$$ and $$3$$ is
5
If $$\overrightarrow a = \left( {\widehat i + \widehat j + \widehat k} \right),\overrightarrow a .\overrightarrow b = 1$$ and $$\overrightarrow a \times \overrightarrow b = \widehat j - \widehat k,$$ then $$\overrightarrow b $$ is
6
If the lines $${{x - 1} \over 2} = {{y + 1} \over 3} = {{z - 1} \over 4}$$ and $$\,{{x - 3} \over 1} = {{y - k} \over 2} = {z \over 1}$$ intersect, then the value of $$k$$ is
7
The unit vector which is orthogonal to the vector $$3\overrightarrow i + 2\overrightarrow j + 6\overrightarrow k $$ and is coplanar with the vectors $$\,2\widehat i + \widehat j + \widehat k$$ and $$\,\widehat i - \widehat j + \widehat k$$$$\,\,\,$$ is
8
The value of the integral $$\int\limits_0^1 {\sqrt {{{1 - x} \over {1 + x}}} dx} $$ is
9
If $$\omega $$ $$\left( { \ne 1} \right)$$ be a cube root of unity and $${\left( {1 + {\omega ^2}} \right)^n} = {\left( {1 + {\omega ^4}} \right)^n},$$ then the least positive value of n is
10
If $$f\left( x \right) = {x^a}\log x$$ and $$f\left( 0 \right) = 0,$$ then the value of $$\alpha $$ for which Rolle's theorem can be applied in $$\left[ {0,1} \right]$$ is
11
If $$f\left( x \right) = {x^3} + b{x^2} + cx + d$$ and $$0 < {b^2} < c,$$ then in $$\left( { - \infty ,\infty } \right)$$
12
The value of $$x$$ for which $$sin\left( {{{\cot }^{ - 1}}\left( {1 + x} \right)} \right) = \cos \left( {{{\tan }^{ - 1}}\,x} \right)$$ is
13
The sides of a triangle are in the ratio $$1:\sqrt 3 :2$$, then the angles of the triangle are in the ratio
14
If $$y$$ is a function of $$x$$ and log $$(x+y)-2xy=0$$, then the value of $$y'(0)$$ is equal to
15
If the line $$62x + \sqrt 6 y = 2$$ touches the hyperbola $${x^2} - 2{y^2} = 4$$, then the point of contact is
16
If tangents are drawn to the ellipse $${x^2} + 2{y^2} = 2,$$ then the locus of the mid-point of the intercept made by the tangents between the coordinate axes is
17
The angle between the tangents drawn from the point $$(1, 4)$$ to the parabola $${y^2} = 4x$$ is
18
If one of the diameters of the circle $${x^2} + {y^2} - 2x - 6y + 6 = 0$$ is a chord to the circle with centre (2, 1), then the radius of the circle is
19
Area of the triangle formed by the line $$x + y = 3$$ and angle bisectors of the pair of straight line $${x^2} - {y^2} + 2y = 1$$ is
20
An infinite G.P. has first term '$$x$$' and sum '$$5$$', then $$x$$ belongs to
21
If $${}^{n - 1}{C_r} = \left( {{k^2} - 3} \right)\,{}^n{C_{r + 1,}}$$ then $$k \in $$
22
For all $$'x',{x^2} + 2ax + 10 - 3a > 0,$$ then the interval in which '$$a$$' lies is
23
If one root is square of the other root of the equation $${x^2} + px + q = 0$$, then the realation between $$p$$ and $$q$$ is
24
Given both $$\theta $$ and $$\phi $$ are acute angles and $$\sin \,\theta = {1 \over 2},\,$$ $$\cos \,\phi = {1 \over 3},$$ then the value of $$\theta + \phi $$ belongs to
Physics
1
Pressure depends on distance as, $$P = {\alpha \over \beta }\exp \left( { - {{\alpha z} \over {k\theta }}} \right)$$, where $$\alpha $$, $$\beta $$ are constants, z in distance, k is Boltzman's constant and $$\theta $$ is temperature. The dimention of $$\beta $$ are
2
A wire of length $$l = 6 \pm 0.06$$ cm and $$r = 0.5 \pm 0.005$$ cm and mass $$m = 0.3 \pm 0.003$$ gm. Maximum percentage error in density is
3
A body starts from rest at time t = 0, the acceleration time graph is
shown in the figure. The maximum velocity attained by the body
will be
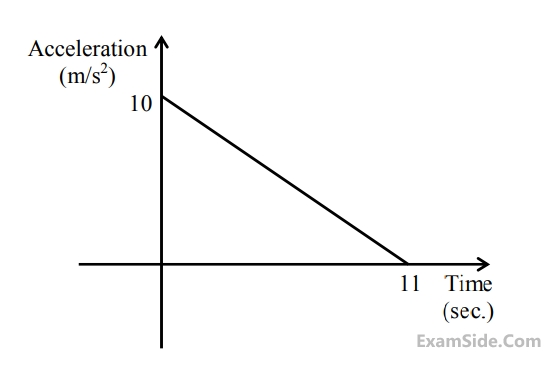

4
A particle starts sliding down a frictionless inclined plane. If Sn is the distance traveled by it from time t = n - 1 sec to t = n sec, the ratio Sn / Sn+1 is
5
A particle is acted by a force F = kx, where k is a +ve constant. Its potential energy at x = 0 is zero. Which
curve correctly represents the variation of potential energy of the block with respect to x