JEE Advanced 2020 Paper 1 Offline
Paper was held on
Sat, Sep 26, 2020 9:00 PM
Chemistry
1
If the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probable, the average, and the root mean square speeds, respectively, is


2
Which of the following liberates O2 upon hydrolysis?
3
A colourless aqueous solution contains nitrates of two metals, X and Y. When it was added to an aqueous solution of NaCl, a white precipitate was formed. This precipitate was found to be partly soluble in hot water to give a residue P and a solution Q. The residue P was soluble in aqueous NH3 and also in excess sodium thiosulphate. The hot solution Q gave a yellow precipitate with KI. The metals X and Y, respectively, are
4
Newman projections P, Q, R and S are shown below :

Which one of the following options represents identical molecules?

Which one of the following options represents identical molecules?
5
Which of the following structures has the IUPAC name
3-ethynyl-2-hydroxy-4-methylhex-3-en-5-ynoic acid?
3-ethynyl-2-hydroxy-4-methylhex-3-en-5-ynoic acid?
6
The Fischer projection of D-erythrose is shown below :

D-erythrose and its isomers are listed as P, Q, R, and S in Column - I. Choose the correct relationship of P, Q, R, and S with D-erythrose from Column - II.


D-erythrose and its isomers are listed as P, Q, R, and S in Column - I. Choose the correct relationship of P, Q, R, and S with D-erythrose from Column - II.

7
In thermodynamics, the p-V work done is given by
$$w = - \int {dV{p_{ext}}} $$
For a system undergoing a particular process, the work done is
$$w = - \int {dV\left( {{{RT} \over {V - b}} - {a \over {{V^2}}}} \right)} $$
This equation is applicable to a
$$w = - \int {dV{p_{ext}}} $$
For a system undergoing a particular process, the work done is
$$w = - \int {dV\left( {{{RT} \over {V - b}} - {a \over {{V^2}}}} \right)} $$
This equation is applicable to a
8
With respect to the compounds I-V, choose the correct statement(s).


9
In the reaction scheme shown below Q, R and S are the major products.

The correct structure of

The correct structure of
10
Choose the correct statement(s) among the following :
11
With respect to hypochlorite, chlorate and perchlorate ions, choose the correct statement(s).
12
The cubic unit cell structure of a compound containing cation M and anion X is shown below. When compared to the anion, the cation has smaller ionic radius. Choose the correct statement(s).


13
5.00 mL of 0.10 M oxalic acid solution taken in a conical flask is titrated against NaOH from a burette using phenolphthalein indicator. The volume of NaOH required for the appearance of permanent faint pink color is tabulated below for five experiments. What is the concentration, in molarity, of the NaOH solution?
| Exp. No. | Vol. of NaOH (mL) |
|---|---|
| 1 | 12.5 |
| 2 | 10.5 |
| 3 | 9.0 |
| 4 | 9.0 |
| 5 | 9.0 |
14
Consider the reaction,
A $$\rightleftharpoons $$ B
at 1000 K. At time t', the temperature of the system was increased to 2000 K and the system was allowed to reach equilibrium. Throughout this experiment the partial pressure of A was maintained at 1 bar. Given, below is the plot of the partial pressure of B with time. What is the ratio of the standard Gibbs energy of the reaction at 1000 K to that at 2000 K?

A $$\rightleftharpoons $$ B
at 1000 K. At time t', the temperature of the system was increased to 2000 K and the system was allowed to reach equilibrium. Throughout this experiment the partial pressure of A was maintained at 1 bar. Given, below is the plot of the partial pressure of B with time. What is the ratio of the standard Gibbs energy of the reaction at 1000 K to that at 2000 K?

15
Consider a 70% efficient hydrogen-oxygen fuel cell working under standard conditions at 1 bar and 298 K. Its cell reaction is
$${H_2}(g) + {1 \over 2}{O_2}(g)\buildrel {} \over \longrightarrow {H_2}O(l)$$
The work derived from the cell on the consumption of 1.0 $$ \times $$ 10$$-$$3 mole of H2(g) is used to compress 1.00 mole of a monoatomic ideal gas in a thermally insulated container. What is the change in the temperature (in K) of the ideal gas?
The standard reduction potentials for the two half-cells are given below :
$${O_2}(g) + 4{H^ + }(aq) + 4{e^ - }\buildrel {} \over \longrightarrow 2{H_2}O(l),$$
$${E^o} = 1.23V$$
$$2{H^ + }(aq) + 2{e^ - }\buildrel {} \over \longrightarrow {H_2}(g),$$
$${E^o} = 0.00\,V$$
Use, $$F = 96500\,C\,mo{l^{ - 1}}$$, $$R = 8.314\,J\,mo{l^{ - 1}}\,{K^{ - 1}}$$.
$${H_2}(g) + {1 \over 2}{O_2}(g)\buildrel {} \over \longrightarrow {H_2}O(l)$$
The work derived from the cell on the consumption of 1.0 $$ \times $$ 10$$-$$3 mole of H2(g) is used to compress 1.00 mole of a monoatomic ideal gas in a thermally insulated container. What is the change in the temperature (in K) of the ideal gas?
The standard reduction potentials for the two half-cells are given below :
$${O_2}(g) + 4{H^ + }(aq) + 4{e^ - }\buildrel {} \over \longrightarrow 2{H_2}O(l),$$
$${E^o} = 1.23V$$
$$2{H^ + }(aq) + 2{e^ - }\buildrel {} \over \longrightarrow {H_2}(g),$$
$${E^o} = 0.00\,V$$
Use, $$F = 96500\,C\,mo{l^{ - 1}}$$, $$R = 8.314\,J\,mo{l^{ - 1}}\,{K^{ - 1}}$$.
16
Aluminium reacts with sulphuric acid to form aluminium sulphate and hydrogen. What is the volume of hydrogen gas in litre (L) produced at 300 K and 1.0 atm pressure, when 5.4 g of aluminium and 50.0 mL of 5.0 M sulphuric acid are combined for the reaction?
(Use molar mass of aluminium as 27.0 g mol$$-$$1, R = 0.082 atm L mol$$-$$1 K$$-$$1)
(Use molar mass of aluminium as 27.0 g mol$$-$$1, R = 0.082 atm L mol$$-$$1 K$$-$$1)
17
$$_{92}^{238}U$$ is known to undergo radioactive decay to form $$_{82}^{206}Pb$$ by emitting alpha and beta particles. A rock initially contained 68 $$ \times $$ 10$$-$$6 g of $$_{92}^{238}U$$. If the number of alpha particles that it would emit during its radioactive decay of $$_{92}^{238}U$$ to $$_{82}^{206}Pb$$ in three half-lives is Z $$ \times $$ 1018, then what is the value of Z?
18
In the following reaction, compound Q is obtained from compound P via an ionic intermediate

What is the degree of unsaturation of Q?

What is the degree of unsaturation of Q?
Mathematics
1
Suppose a, b denote the distinct real roots of the quadratic polynomial x2 + 20x $$-$$ 2020 and suppose c, d denote the distinct complex roots of the quadratic polynomial x2 $$-$$ 20x + 2020. Then the value of
ac(a $$-$$ c) + ad(a $$-$$ d) + bc(b $$-$$ c) + bd(b $$-$$ d) is
ac(a $$-$$ c) + ad(a $$-$$ d) + bc(b $$-$$ c) + bd(b $$-$$ d) is
2
If the function f : R $$ \to $$ R is defined by f(x) = |x| (x $$-$$ sin x), then which of the following statements is TRUE?
3
Let the functions f : R $$ \to $$ R and g : R $$ \to $$ R be defined by
f(x) = ex $$-$$ 1 $$-$$ e$$-$$|x $$-$$ 1|
and g(x) = $${1 \over 2}$$(ex $$-$$ 1 + e1 $$-$$ x).
The the area of the region in the first quadrant bounded by the curves y = f(x), y = g(x) and x = 0 is
f(x) = ex $$-$$ 1 $$-$$ e$$-$$|x $$-$$ 1|
and g(x) = $${1 \over 2}$$(ex $$-$$ 1 + e1 $$-$$ x).
The the area of the region in the first quadrant bounded by the curves y = f(x), y = g(x) and x = 0 is
4
Let a, b and $$\lambda $$ be positive real numbers. Suppose P is an end point of the latus return of the
parabola y2 = 4$$\lambda $$x, and suppose the ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
parabola y2 = 4$$\lambda $$x, and suppose the ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
5
Let C1 and C2 be two biased coins such that the probabilities of getting head in a single toss are $${{2 \over 3}}$$ and $${{1 \over 3}}$$, respectively. Suppose $$\alpha $$ is the number of heads that appear when C1 is tossed twice, independently, and suppose $$\beta $$ is the number of heads that appear when C2 is tossed twice, independently. Then the probability that the roots of the quadratic polynomial x2 $$-$$ ax + $$\beta $$ are real and equal, is
6
Consider the rectangles lying the region
$$\left\{ {(x,y) \in R \times R:0\, \le \,x\, \le \,{\pi \over 2}} \right.$$ and $$\left. {0\, \le \,y\, \le \,2\sin (2x)} \right\}$$
and having one side on the X-axis. The area of the rectangle which has the maximum perimeter among all such rectangles, is
$$\left\{ {(x,y) \in R \times R:0\, \le \,x\, \le \,{\pi \over 2}} \right.$$ and $$\left. {0\, \le \,y\, \le \,2\sin (2x)} \right\}$$
and having one side on the X-axis. The area of the rectangle which has the maximum perimeter among all such rectangles, is
7
Let the function f : R $$ \to $$ R be defined by f(x) = x3 $$-$$ x2 + (x $$-$$ 1)sin x and let g : R $$ \to $$ R be an arbitrary function. Let fg : R $$ \to $$ R be the product function defined by (fg)(x) = f(x)g(x). Then which of the following statements is/are TRUE?
8
Let M be a 3 $$ \times $$ 3 invertible matrix with real entries and let I denote the 3 $$ \times $$ 3 identity matrix. If M$$-$$1 = adj(adj M), then which of the following statements is/are ALWAYS TRUE?
9
Let S be the set of all complex numbers z
satisfying |z2 + z + 1| = 1. Then which of the following statements is/are TRUE?
satisfying |z2 + z + 1| = 1. Then which of the following statements is/are TRUE?
10
Let x, y and z be positive real numbers. Suppose x, y and z are the lengths of the sides of a triangle opposite to its angles X, Y, and Z, respectively. If
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$, then which of the following statements is/are TRUE?
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$, then which of the following statements is/are TRUE?
11
Let L1 and L2 be the following straight lines.
$${L_1}:{{x - 1} \over 1} = {y \over { - 1}} = {{z - 1} \over 3}$$ and $${L_2}:{{x - 1} \over { - 3}} = {y \over { - 1}} = {{z - 1} \over 1}$$.
Suppose the straight line
$$L:{{x - \alpha } \over l} = {{y - 1} \over m} = {{z - \gamma } \over { - 2}}$$
lies in the plane containing L1 and L2 and passes through the point of intersection of L1 and L2. If the line L bisects the acute angle between the lines L1 and L2, then which of the following statements is/are TRUE?
$${L_1}:{{x - 1} \over 1} = {y \over { - 1}} = {{z - 1} \over 3}$$ and $${L_2}:{{x - 1} \over { - 3}} = {y \over { - 1}} = {{z - 1} \over 1}$$.
Suppose the straight line
$$L:{{x - \alpha } \over l} = {{y - 1} \over m} = {{z - \gamma } \over { - 2}}$$
lies in the plane containing L1 and L2 and passes through the point of intersection of L1 and L2. If the line L bisects the acute angle between the lines L1 and L2, then which of the following statements is/are TRUE?
12
Which of the following inequalities is/are TRUE?
13
Let m be the minimum possible value of $${\log _3}({3^{{y_1}}} + {3^{{y_2}}} + {3^{{y_3}}})$$, where $${y_1},{y_2},{y_3}$$ are real numbers for which $${{y_1} + {y_2} + {y_3}}$$ = 9. Let M be the maximum possible value of $$({\log _3}{x_1} + {\log _3}{x_2} + {\log _3}{x_3})$$, where $${x_1},{x_2},{x_3}$$ are positive real numbers for which $${{x_1} + {x_2} + {x_3}}$$ = 9. Then the value of $${\log _2}({m^3}) + {\log _3}({M^2})$$ is ...........
14
Let a1, a2, a3, .... be a sequence of positive integers in arithmetic progression with common difference 2. Also, let b1, b2, b3, .... be a sequence of positive integers in geometric progression with common ratio 2. If a1 = b1 = c, then the number of all possible values of c, for which the equality 2(a1 + a2 + ... + an) = b1 + b2 + ... + bn holds for some positive integer n, is ...........
15
Let f : [0, 2] $$ \to $$ R be the function defined by
$$f(x) = (3 - \sin (2\pi x))\sin \left( {\pi x - {\pi \over 4}} \right) - \sin \left( {3\pi x + {\pi \over 4}} \right)$$
If $$\alpha ,\,\beta \in [0,2]$$ are such that $$\{ x \in [0,2]:f(x) \ge 0\} = [\alpha ,\beta ]$$, then the value of $$\beta - \alpha $$ is ..........
$$f(x) = (3 - \sin (2\pi x))\sin \left( {\pi x - {\pi \over 4}} \right) - \sin \left( {3\pi x + {\pi \over 4}} \right)$$
If $$\alpha ,\,\beta \in [0,2]$$ are such that $$\{ x \in [0,2]:f(x) \ge 0\} = [\alpha ,\beta ]$$, then the value of $$\beta - \alpha $$ is ..........
16
In a triangle PQR, let a = QR, b = RP, and c = PQ. If |a| = 3, |b| = 4
and $${{a\,.(\,c - \,b)} \over {c\,.\,(a - \,b)}} = {{|a|} \over {|a| + |b|}}$$, then the value of |a $$ \times $$ b|2 is ......
and $${{a\,.(\,c - \,b)} \over {c\,.\,(a - \,b)}} = {{|a|} \over {|a| + |b|}}$$, then the value of |a $$ \times $$ b|2 is ......
17
For a polynomial g(x) with real coefficients, let mg denote the number of distinct real roots of g(x). Suppose S is the set of polynomials with real coefficients defined by
$$S = \{ {({x^2} - 1)^2}({a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3}):{a_0},{a_1},{a_2},{a_3} \in R\} $$;
For a polynomial f, let f' and f'' denote its first and second order derivatives, respectively. Then the minimum possible value of (mf' + mf''), where f $$ \in $$ S, is ..............
$$S = \{ {({x^2} - 1)^2}({a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3}):{a_0},{a_1},{a_2},{a_3} \in R\} $$;
For a polynomial f, let f' and f'' denote its first and second order derivatives, respectively. Then the minimum possible value of (mf' + mf''), where f $$ \in $$ S, is ..............
18
let e denote the base of the natural logarithm. The value of the real number a for which the right hand limit
$$\mathop {\lim }\limits_{x \to {0^ + }} {{{{(1 - x)}^{1/x}} - {e^{ - 1}}} \over {{x^a}}}$$
is equal to a non-zero real number, is .............
$$\mathop {\lim }\limits_{x \to {0^ + }} {{{{(1 - x)}^{1/x}} - {e^{ - 1}}} \over {{x^a}}}$$
is equal to a non-zero real number, is .............
Physics
1
A small roller of diameter 20 cm has an axle of diameter 10 cm (see figure below on the left). It is
on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale
on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it
moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has
moved 50 cm, the position of the scale will look like (figures are schematic and not drawn to scale)


2
A football of radius R is kept on a hole of radius r (r < R) made on a plank kept horizontally. One
end of the plank is now lifted so that it gets tilted making an angle $$\theta $$ from the horizontal as shown in
the figure below. The maximum value of $$\theta $$ so that the football does not start rolling down the plank
satisfies (figure is schematic and not drawn to scale)
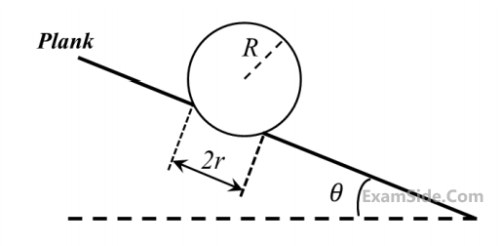

3
A stationary tuning fork is in resonance with an air column in a pipe. If the tuning fork is moved with
a speed of 2 ms−1
in front of the open end of the pipe and parallel to it, the length of the pipe should
be changed for the resonance to occur with the moving tuning fork. If the speed of sound in air is
320 ms−1, the smallest value of the percentage change required in the length of the pipe is
____________.
4
A circular disc of radius R carries surface charge density
$$\sigma \left( r \right) = {\sigma _0}\left( {1 - {r \over R}} \right)$$, where $$\sigma $$0 is a constant and r is the distance from the center of the disc. Electric flux through a large spherical surface that encloses the charged disc completely is $$\phi $$0. Electric flux through another spherical surface of radius $${R \over 4}$$ and concentric with the disc is $$\phi $$. Then the ratio $${{{\phi _0}} \over \phi }$$ is ________.
$$\sigma \left( r \right) = {\sigma _0}\left( {1 - {r \over R}} \right)$$, where $$\sigma $$0 is a constant and r is the distance from the center of the disc. Electric flux through a large spherical surface that encloses the charged disc completely is $$\phi $$0. Electric flux through another spherical surface of radius $${R \over 4}$$ and concentric with the disc is $$\phi $$. Then the ratio $${{{\phi _0}} \over \phi }$$ is ________.
5
As shown schematically in the figure, two vessels contain water solutions (at temperature T) of
potassium permanganate (KMnO4) of different concentrations n1 and n2 (n1 > n2) molecules per
unit volume with $$\Delta $$n = (n1 − n2) << n1. When they are connected by a tube of small length l and
cross-sectional area S, KMnO4 starts to diffuse from the left to the right vessel through the tube.
Consider the collection of molecules to behave as dilute ideal gases and the difference in their partial
pressure in the two vessels causing the diffusion. The speed v of the molecules is limited by the
viscous force −$$\beta $$v on each molecule, where $$\beta $$ is a constant. Neglecting all terms of the order ($$\Delta $$n)2,
which of the following is/are correct? (kB is the Boltzmann constant)


6
When water is filled carefully in a glass, one can fill it to a height h above the rim of the glass due to
the surface tension of water. To calculate h just before water starts flowing, model the shape of the
water above the rim as a disc of thickness h having semicircular edges, as shown schematically in the
figure. When the pressure of water at the bottom of this disc exceeds what can be withstood due to
the surface tension, the water surface breaks near the rim and water starts flowing from there. If the
density of water, its surface tension and the acceleration
due to gravity are 103 kg m−3 , 0.07 Nm−1 and 10 ms−2 , respectively, the value of h (in mm) is _________.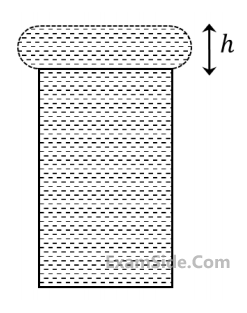
due to gravity are 103 kg m−3 , 0.07 Nm−1 and 10 ms−2 , respectively, the value of h (in mm) is _________.

7
Put a uniform meter scale horizontally on your extended index fingers with the left one at 0.00 cm
and the right one at 90.00 cm. When you attempt to move both the fingers slowly towards the center,
initially only the left finger slips with respect to the scale and the right finger does not. After some
distance, the left finger stops and the right one starts slipping. Then the right finger stops at a distance
xR from the center (50.00 cm) of the scale and the left one starts slipping again. This happens
because of the difference in the frictional forces on the two fingers. If the coefficients of static and
dynamic friction between the fingers and the scale are 0.40 and 0.32, respectively, the value of xR (in
cm) is ______.
8
One end of a spring of negligible unstretched length and spring constant k is fixed at the origin (0, 0).
A point particle of mass m carrying a positive charge q is attached at its other end. The entire system
is kept on a smooth horizontal surface. When a point dipole $$\overrightarrow p $$ pointing towards the charge q is fixed
at the origin, the spring gets stretched to a length l and attains a new equilibrium position (see figure
below). If the point mass is now displaced slightly by $$\Delta $$l << l from its equilibrium position and
released, it is found to oscillate at frequency $${1 \over \delta }\sqrt {{k \over m}} $$. The value of $$\delta $$ is ______.


9
Consider one mole of helium gas enclosed in a container at initial pressure P1 and volume V1. It
expands isothermally to volume 4V1. After this, the gas expands adiabatically and its volume becomes
32V1. The work done by the gas during isothermal and adiabatic expansion processes are Wiso and
Wadia, respectively. If the ratio $${{{W_{iso}}} \over {{W_{adia}}}}$$ = f ln 2, then f is ______.
10
Shown in the figure is a semicircular metallic strip that has thickness t and resistivity $$\rho $$. Its inner
radius is R1 and outer radius is R2. If a voltage V0 is applied between its two ends, a current I flows
in it. In addition, it is observed that a transverse voltage $$\Delta $$V develops between its inner and outer
surfaces due to purely kinetic effects of moving electrons (ignore any role of the magnetic field due
to the current). Then (figure is schematic and not drawn to scale)


11
A particle of mass m moves in circular orbits with potential energy V(r) = Fr, where F is a positive
constant and r is its distance from the origin. Its energies are calculated using the Bohr model. If the
radius of the particle’s orbit is denoted by R and its speed and energy are denoted by v and E,
respectively, then for the nth orbit (here h is the Planck’s constant)
12
Sometimes it is convenient to construct a system of units so that all quantities can be expressed in
terms of only one physical quantity. In one such system, dimensions of different quantities are given
in terms of a quantity X as follows: [position] = [X$$\alpha $$]; [speed] = [X$$\beta $$
]; [acceleration] = [Xp]; [linear
momentum] = [Xq]; [force] = [Xr]. Then
13
The filament of a light bulb has surface area 64 mm2
. The filament can be considered as a black
body at temperature 2500 K emitting radiation like a point source when viewed from far. At night
the light bulb is observed from a distance of 100 m. Assume the pupil of the eyes of the observer to
be circular with radius 3 mm. Then
(Take Stefan-Boltzmann constant = 5.67 $$ \times $$ 10−8 Wm−2K−4 , Wien’s displacement constant = 2.90 $$ \times $$ 10−3 m-K, Planck’s constant = 6.63 $$ \times $$ 10−34 Js, speed of light in vacuum = 3.00 $$ \times $$ 108 ms−1)
(Take Stefan-Boltzmann constant = 5.67 $$ \times $$ 10−8 Wm−2K−4 , Wien’s displacement constant = 2.90 $$ \times $$ 10−3 m-K, Planck’s constant = 6.63 $$ \times $$ 10−34 Js, speed of light in vacuum = 3.00 $$ \times $$ 108 ms−1)
14
An open-ended U-tube of uniform cross-sectional area contains water (density 103 kg m−3
). Initially the
water level stands at 0.29 m from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of
density 800 kg m−3
is added to the left arm until its length is 0.1 m, as shown in the schematic figure
below. The ratio $$\left( {{{{h_1}} \over {{h_2}}}} \right)$$ of the heights of the liquid in the two arms is :


15
A light disc made of aluminium (a nonmagnetic material) is kept horizontally and is free to rotate
about its axis as shown in the figure. A strong magnet is held vertically at a point above the disc away
from its axis. On revolving the magnet about the axis of the disc, the disc will (figure is schematic
and not drawn to scale)


16
A circular coil of radius R and N turns has negligible resistance. As shown in the schematic figure,
its two ends are connected to two wires and it is hanging by those wires with its plane being vertical.
The wires are connected to a capacitor with charge Q through a switch. The coil is in a horizontal
uniform magnetic field Bo parallel to the plane of the coil. When the switch is closed, the capacitor
gets discharged through the coil in a very short time. By the time the capacitor is discharged fully,
magnitude of the angular momentum gained by the coil will be (assume that the discharge time is so
short that the coil has hardly rotated during this time)


17
A parallel beam of light strikes a piece of transparent glass having cross section as shown in the figure
below. Correct shape of the emergent wavefront will be (figures are schematic and not drawn to
scale)


18
A uniform electric field, $$\overrightarrow E = - 400\sqrt 3 \widehat y$$ NC−1
is applied in a region. A charged particle of mass m
carrying positive charge q is projected in this region with an initial speed of 2$$\sqrt {10} $$ $$ \times $$ 106 ms−1
. This
particle is aimed to hit a target T, which is 5 m away from its entry point into the field as shown
schematically in the figure.
Take $${q \over m}$$ = 1010 Ckg−1 . Then
Take $${q \over m}$$ = 1010 Ckg−1 . Then
