Chemistry


(L= H2NCH2CH2O-) is (are)...
The increasing order of atomic radii of the following group 13 elements is
On complete hydrogenation, natural rubber produces
Among [Ni(CO)4], [NiCl4]2$$-$$, [Co(NH3)4)Cl2]Cl, Na3[CoF6], Na2O2 and CsO2, the total number of paramagnetic compound is
The correct statements about of the following reaction sequence is (are)
Cumene (C9H12) $$\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{(ii)\,{H_3}{O^ + }}^{(i)\,{O_2}}} $$ P $$\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{}^{CHC{l_3}/NaOH}} $$ Q (major) + R (minor)
Q $$\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{PhC{H_2}Br}^{NaOH}} $$ S
Mathematics
$$ = 10P$$ (computer turns out to be defective given that it is produced in plant $${T_2}$$),
where $$P(E)$$ denotes the probability of an event $$E$$. A computer produced in the factory is randomly selected and it does not turn out to be defective. Then the probability that it is produced in plant $${T_2}$$ is
$$\int\limits_0^x {{{{t^2}} \over {1 + {t^4}}}} dt = 2x - 1$$
$$\left( {{x^2} + xy + 4x + 2y + 4} \right){{dy} \over {dx}} - {y^2} = 0,$$ $$x>0,$$ passes through the
point $$(1,3)$$. Then the solution curve
If $${{s - x} \over 4} = {{s - y} \over 3} = {{s - z} \over 2}$$ and area of incircle of the triangle $$XYZ$$ is $${{8\pi } \over 3}$$, then
Let $$f:(0,\infty ) \to R$$ be a differentiable function such that $$f'(x) = 2 - {{f(x)} \over x}$$ for all $$x \in (0,\infty )$$ and $$f(1) \ne 1$$. Then
Let $$P = \left[ {\matrix{ 3 & { - 1} & { - 2} \cr 2 & 0 & \alpha \cr 3 & { - 5} & 0 \cr } } \right]$$, where $$\alpha$$ $$\in$$ R. Suppose $$Q = [{q_{ij}}]$$ is a matrix such that PQ = kl, where k $$\in$$ R, k $$\ne$$ 0 and I is the identity matrix of order 3. If $${q_{23}} = - {k \over 8}$$ and $$\det (Q) = {{{k^2}} \over 2}$$, then
The total number of distinct x $$\in$$ R for which
$$\left| {\matrix{ x & {{x^2}} & {1 + {x^3}} \cr {2x} & {4{x^2}} & {1 + 8{x^3}} \cr {3x} & {9{x^2}} & {1 + 27{x^3}} \cr } } \right| = 10$$ is ______________.
Let $$z = {{ - 1 + \sqrt 3 i} \over 2}$$, where $$i = \sqrt { - 1} $$, and r, s $$\in$$ {1, 2, 3}. Let $$P = \left[ {\matrix{ {{{( - z)}^r}} & {{z^{2s}}} \cr {{z^{2s}}} & {{z^r}} \cr } } \right]$$ and I be the identity matrix of order 2. Then the total number of ordered pairs (r, s) for which P2 = $$-$$I is ____________.
Let $$\alpha$$, $$\beta$$ $$\in$$ R be such that $$\mathop {\lim }\limits_{x \to 0} {{{x^2}\sin (\beta x)} \over {\alpha x - \sin x}} = 1$$. Then 6($$\alpha$$ + $$\beta$$) equals _________.
Physics

| $$\lambda \left( {\mu m} \right)$$ | V0(Volt) |
|---|---|
| 0.3 | 2.0 |
| 0.4 | 1.0 |
| 0.5 | 0.4 |
Given that c = 3 $$ \times $$ 108 ms-1 and e = 1.6 $$ \times $$ 10-19 C, Planck's constant (in units of J-s) found from such an experiment is) :
The temperature of water fed into the device cannot exceed 30°C and the entire stored 120 litres of water is initially cooled to 10°C. The entire system is thermally insulated. The minimum value of P (in watts) for which the device can be operated for 3 hours is :
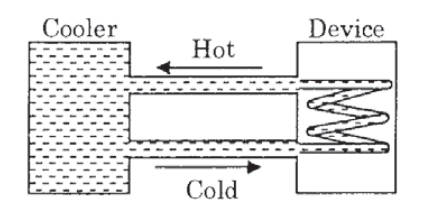
(Specific heat of water is 4.2 kJ kg−1 K−1 and the density of water is 1000 kg m−3)

Let v(t) represent the beat frequency measured by a person sitting in the car at time t. Let vP, vQ and vR be the beat frequencies measured at locations P, Q and R respectively. The speed of sound in air is 330 ms$$-$$1. Which of the following statement(s) is (are) true regarding the sound heard by the person?

Which of the following statement(s) is (are) true?
Taking hc = 1.237 $$\times$$ 10$$-$$6 eVm and the ground state energy of hydrogen atom as $$-$$ 13.6 eV, the number of lines present in the emission spectrum is