Chemistry
A closed vessel contains $10 \mathrm{~g}$ of an ideal gas $\mathbf{X}$ at $300 \mathrm{~K}$, which exerts $2 \mathrm{~atm}$ pressure. At the same temperature, $80 \mathrm{~g}$ of another ideal gas $\mathbf{Y}$ is added to it and the pressure becomes $6 \mathrm{~atm}$. The ratio of root mean square velocities of $\mathbf{X}$ and $\mathbf{Y}$ at $300 \mathrm{~K}$ is
At room temperature, disproportionation of an aqueous solution of in situ generated nitrous acid $\left(\mathrm{HNO}_2\right)$ gives the species

Among the following options, select the option in which each complex in Set-I shows geometrical isomerism and the two complexes in Set-II are ionization isomers of each other.
$$ \text { [en }=\mathrm{H}_2 \mathrm{NCH}_2 \mathrm{CH}_2 \mathrm{NH}_2 \text { ] } $$
Among the following, the correct statement(s) for electrons in an atom is(are)
Reaction of iso-propylbenzene with $\mathrm{O}_2$ followed by the treatment with $\mathrm{H}_3 \mathrm{O}^{+}$forms phenol and a by-product $\mathbf{P}$. Reaction of $\mathbf{P}$ with 3 equivalents of $\mathrm{Cl}_2$ gives compound $\mathbf{Q}$. Treatment of $\mathbf{Q}$ with $\mathrm{Ca}(\mathrm{OH})_2$ produces compound $\mathbf{R}$ and calcium salt $\mathbf{S}$.
The correct statement(s) regarding $\mathbf{P}, \mathbf{Q}, \mathbf{R}$ and $\mathbf{S}$ is(are)
The option(s) in which at least three molecules follow Octet Rule is(are)
Consider the following volume-temperature $(\mathrm{V}-\mathrm{T})$ diagram for the expansion of 5 moles of an ideal monoatomic gas.

Considering only $\mathrm{P}-\mathrm{V}$ work is involved, the total change in enthalpy (in Joule) for the transformation of state in the sequence $\mathbf{X} \rightarrow \mathbf{Y} \rightarrow \mathbf{Z}$ is ____________.
[Use the given data: Molar heat capacity of the gas for the given temperature range, $\mathrm{C}_{\mathrm{V}, \mathrm{m}}=12 \mathrm{~J} \mathrm{~K}^{-1}$ $\mathrm{mol}^{-1}$ and gas constant, $\left.\mathrm{R}=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right]$
Consider the following reaction,
$$ 2 \mathrm{H}_2(\mathrm{~g})+2 \mathrm{NO}(\mathrm{g}) \rightarrow \mathrm{N}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) $$
which follows the mechanism given below :
$$ \begin{array}{ll} 2 \mathrm{NO}(\mathrm{g}) \stackrel{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \mathrm{N}_2 \mathrm{O}_2(\mathrm{~g}) & \text { (fast equlibrium) } \\\\ \mathrm{N}_2 \mathrm{O}_2(\mathrm{~g})+\mathrm{H}_2(\mathrm{~g}) \xrightarrow{k_2} \mathrm{~N}_2 \mathrm{O}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) & \text { (slow reaction) } \\\\ \mathrm{N}_2 \mathrm{O}(\mathrm{g})+\mathrm{H}_2(\mathrm{~g}) \xrightarrow{k_3} \mathrm{~N}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) & \text { (fast reaction) } \end{array} $$
The order of the reaction is __________.
Complete reaction of acetaldehyde with excess formaldehyde, upon heating with conc. $\mathrm{NaOH}$ solution, gives $\mathbf{P}$ and $\mathbf{Q}$. Compound $\mathbf{P}$ does not give Tollens' test, whereas $\mathbf{Q}$ on acidification gives positive Tollens' test. Treatment of $\mathbf{P}$ with excess cyclohexanone in the presence of catalytic amount of $p$-toluenesulfonic acid (PTSA) gives product $\mathbf{R}$.
Sum of the number of methylene groups $\left(-\mathrm{CH}_2-\right)$ and oxygen atoms in $\mathbf{R}$ is __________.
Among $\mathrm{V}(\mathrm{CO})_6, \mathrm{Cr}(\mathrm{CO})_5, \mathrm{Cu}(\mathrm{CO})_3, \mathrm{Mn}(\mathrm{CO})_5, \mathrm{Fe}(\mathrm{CO})_5,\left[\mathrm{Co}(\mathrm{CO})_3\right]^{3-},\left[\mathrm{Cr}(\mathrm{CO})_4\right]^{4-}$, and $\operatorname{Ir}(\mathrm{CO})_3$, the total number of species isoelectronic with $\mathrm{Ni}(\mathrm{CO})_4$ is _________.
[Given, atomic number: $\mathrm{V}=23, \mathrm{Cr}=24, \mathrm{Mn}=25, \mathrm{Fe}=26, \mathrm{Co}=27, \mathrm{Ni}=28, \mathrm{Cu}=29, \mathrm{Ir}=77$ ]
In the following reaction sequence, the major product $\mathbf{P}$ is formed.

Glycerol reacts completely with excess $\mathbf{P}$ in the presence of an acid catalyst to form $\mathbf{Q}$. Reaction of $\mathbf{Q}$ with excess $\mathrm{NaOH}$ followed by the treatment with $\mathrm{CaCl}_2$ yields Ca-soap $\mathbf{R}$, quantitatively. Starting with one mole of $\mathbf{Q}$, the amount of $\mathbf{R}$ produced in gram is __________.
[Given, atomic weight: $\mathrm{H}=1, \mathrm{C}=12, \mathrm{~N}=14, \mathrm{O}=16, \mathrm{Na}=23, \mathrm{Cl}=35, \mathrm{Ca}=40$ ]
Among the following complexes, the total number of diamagnetic species is ___________.
$\left[\mathrm{Mn}\left(\mathrm{NH}_3\right)_6\right]^{3+},\left[\mathrm{MnCl}_6\right]^{3-},\left[\mathrm{FeF}_6\right]^{3-},\left[\mathrm{CoF}_6\right]^{3-},\left[\mathrm{Fe}\left(\mathrm{NH}_3\right)_6\right]^{3+}$, and $\left[\mathrm{Co}(\mathrm{en})_3\right]^{3+}$
[Given, atomic number: $\mathrm{Mn}=25, \mathrm{Fe}=26, \mathrm{Co}=27$;
$$ \text { en } \left.=\mathrm{H}_2 \mathrm{NCH}_2 \mathrm{CH}_2 \mathrm{NH}_2\right] $$
In a conductometric titration, small volume of titrant of higher concentration is added stepwise to a larger volume of titrate of much lower concentration, and the conductance is measured after each addition.
The limiting ionic conductivity $\left(\Lambda_0\right)$ values (in $\mathrm{mS} \mathrm{m}{ }^2 \mathrm{~mol}^{-1}$ ) for different ions in aqueous solutions are given below:
$$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \text { Ions } & \mathrm{Ag}^{+} & \mathrm{K}^{+} & \mathrm{Na}^{+} & \mathrm{H}^{+} & \mathrm{NO}_3^{-} & \mathrm{Cl}^{-} & \mathrm{SO}_4^{2-} & \mathrm{OH}^{-} & \mathrm{CH}_3 \mathrm{COO}^{-} \\ \hline \Lambda_0 & 6.2 & 7.4 & 5.0 & 35.0 & 7.2 & 7.6 & 16.0 & 19.9 & 4.1 \\ \hline \end{array} $$
For different combinations of titrates and titrants given in List-I, the graphs of 'conductance' versus 'volume of titrant' are given in List-II.
Match each entry in List-I with the appropriate entry in List-II and choose the correct option.
| LIST-I | LIST-II |
|---|---|
| (P) Titrate: KCl Titrant: AgNO$_3$ |

|
| (Q) Titrate: AgNO$_3$ Titrant: KCl |

|
| (R) Titrate: NaOH Titrant: HCl |

|
| (S) Titrate: NaOH Titrant: CH$_3$COOH |

|

|
Based on VSEPR model, match the xenon compounds given in List-I with the corresponding geometries and the number of lone pairs on xenon given in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) XeF$_2$ | (1) Trigonal bipyramidal and two lone pair of electrons |
| (Q) XeF$_4$ | (2) Tetrahedral and one lone pair of electrons |
| (R) XeO$_3$ | (3) Octahedral and two lone pair of electrons |
| (S) XeO$_3$F$_2$ | (4) Trigonal bipyramidal and no lone pair of electrons |
| (5) Trigonal bipyramidal and three lone pair of electrons |
List-I contains various reaction sequences and List-II contains the possible products. Match each entry in List-I with the appropriate entry in List-II and choose the correct option.
| List-I | List-II |
|---|---|

|

|

|

|

|

|

|

|

|
List-I contains various reaction sequences and List-II contains different phenolic compounds. Match each entry in List-I with the appropriate entry in List-II and choose the correct option.
| List-I | List-II |
|---|---|

|

|

|

|

|

|

|

|

|
Mathematics
Let $f(x)$ be a continuously differentiable function on the interval $(0, \infty)$ such that $f(1)=2$ and
$$ \lim\limits_{t \rightarrow x} \frac{t^{10} f(x)-x^{10} f(t)}{t^9-x^9}=1 $$
for each $x>0$. Then, for all $x>0, f(x)$ is equal to :
A student appears for a quiz consisting of only true-false type questions and answers all the questions. The student knows the answers of some questions and guesses the answers for the remaining questions. Whenever the student knows the answer of a question, he gives the correct answer. Assume that the probability of the student giving the correct answer for a question, given that he has guessed it, is $\frac{1}{2}$. Also assume that the probability of the answer for a question being guessed, given that the student's answer is correct, is $\frac{1}{6}$. Then the probability that the student knows the answer of a randomly chosen question is :
Let $\frac{\pi}{2} < x < \pi$ be such that $\cot x=\frac{-5}{\sqrt{11}}$. Then
$$ \left(\sin \frac{11 x}{2}\right)(\sin 6 x-\cos 6 x)+\left(\cos \frac{11 x}{2}\right)(\sin 6 x+\cos 6 x) $$
is equal to :
Consider the ellipse $\frac{x^2}{9}+\frac{y^2}{4}=1$. Let $S(p, q)$ be a point in the first quadrant such that $\frac{p^2}{9}+\frac{q^2}{4}>1$. Two tangents are drawn from $S$ to the ellipse, of which one meets the ellipse at one end point of the minor axis and the other meets the ellipse at a point $T$ in the fourth quadrant. Let $R$ be the vertex of the ellipse with positive $x$-coordinate and $O$ be the center of the ellipse. If the area of the triangle $\triangle O R T$ is $\frac{3}{2}$, then which of the following options is correct?
Let $\mathbb{R}^2$ denote $\mathbb{R} \times \mathbb{R}$. Let
$$ S=\left\{(a, b, c): a, b, c \in \mathbb{R} \text { and } a x^2+2 b x y+c y^2>0 \text { for all }(x, y) \in \mathbb{R}^2-\{(0,0)\}\right\} . $$
Then which of the following statements is (are) TRUE?
Let $\mathbb{R}^3$ denote the three-dimensional space. Take two points $P=(1,2,3)$ and $Q=(4,2,7)$. Let $\operatorname{dist}(X, Y)$ denote the distance between two points $X$ and $Y$ in $\mathbb{R}^3$. Let
$$ \begin{gathered} S=\left\{X \in \mathbb{R}^3:(\operatorname{dist}(X, P))^2-(\operatorname{dist}(X, Q))^2=50\right\} \text { and } \\ T=\left\{Y \in \mathbb{R}^3:(\operatorname{dist}(Y, Q))^2-(\operatorname{dist}(Y, P))^2=50\right\} . \end{gathered} $$
Then which of the following statements is (are) TRUE?
Let $a=3 \sqrt{2}$ and $b=\frac{1}{5^{1 / 6} \sqrt{6}}$. If $x, y \in \mathbb{R}$ are such that
$$ \begin{aligned} & 3 x+2 y=\log _a(18)^{\frac{5}{4}} \quad \text { and } \\ & 2 x-y=\log _b(\sqrt{1080}), \end{aligned} $$
then $4 x+5 y$ is equal to __________.
Let $f(x)=x^4+a x^3+b x^2+c$ be a polynomial with real coefficients such that $f(1)=-9$. Suppose that $i \sqrt{3}$ is a root of the equation $4 x^3+3 a x^2+2 b x=0$, where $i=\sqrt{-1}$. If $\alpha_1, \alpha_2, \alpha_3$, and $\alpha_4$ are all the roots of the equation $f(x)=0$, then $\left|\alpha_1\right|^2+\left|\alpha_2\right|^2+\left|\alpha_3\right|^2+\left|\alpha_4\right|^2$ is equal to ____________.
Let $S=\left\{A=\left(\begin{array}{lll}0 & 1 & c \\ 1 & a & d \\ 1 & b & e\end{array}\right): a, b, c, d, e \in\{0,1\}\right.$ and $\left.|A| \in\{-1,1\}\right\}$, where $|A|$ denotes the determinant of $A$. Then the number of elements in $S$ is __________.
A group of 9 students, $s_1, s_2, \ldots, s_9$, is to be divided to form three teams $X, Y$, and $Z$ of sizes 2,3 , and 4 , respectively. Suppose that $s_1$ cannot be selected for the team $X$, and $s_2$ cannot be selected for the team $Y$. Then the number of ways to form such teams, is ____________.
Let $\overrightarrow{O P}=\frac{\alpha-1}{\alpha} \hat{i}+\hat{j}+\hat{k}, \overrightarrow{O Q}=\hat{i}+\frac{\beta-1}{\beta} \hat{j}+\hat{k}$ and $\overrightarrow{O R}=\hat{i}+\hat{j}+\frac{1}{2} \hat{k}$ be three vectors, where $\alpha, \beta \in \mathbb{R}-\{0\}$ and $O$ denotes the origin. If $(\overrightarrow{O P} \times \overrightarrow{O Q}) \cdot \overrightarrow{O R}=0$ and the point $(\alpha, \beta, 2)$ lies on the plane $3 x+3 y-z+l=0$, then the value of $l$ is ____________.
Let $X$ be a random variable, and let $P(X=x)$ denote the probability that $X$ takes the value $x$. Suppose that the points $(x, P(X=x)), x=0,1,2,3,4$, lie on a fixed straight line in the $x y$-plane, and $P(X=x)=0$ for all $x \in \mathbb{R}-\{0,1,2,3,4\}$. If the mean of $X$ is $\frac{5}{2}$, and the variance of $X$ is $\alpha$, then the value of $24 \alpha$ is _____________.
Match each entry in List-I to the correct entry in List-II.
| List-I | List-II |
|---|---|
| (P) The number of matrices $ M = (a_{ij})_{3x3} $ with all entries in $ T $ such that $ R_i = C_j = 0 $ for all $ i, j $, is | (1) 1 |
| (Q) The number of symmetric matrices $ M = (a_{ij})_{3x3} $ with all entries in $ T $ such that $ C_j = 0 $ for all $ j $, is | (2) 12 |
| (R) Let $ M = (a_{ij})_{3x3} $ be a skew symmetric matrix such that $ a_{ij} \in T $ for $ i > j $. Then the number of elements in the set $ \left\{ \begin{pmatrix} x \\ y \\ z \end{pmatrix} : x, y, z \in \mathbb{R}, M \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} a_{12} \\ 0 \\ a_{13} \end{pmatrix} \right\} $ is |
(3) infinite |
| (S) Let $ M = (a_{ij})_{3x3} $ be a matrix with all entries in $ T $ such that $ R_i = 0 $ for all $ i $. Then the absolute value of the determinant of $ M $ is | (4) 6 |
The correct option is
Let the straight line $y=2 x$ touch a circle with center $(0, \alpha), \alpha>0$, and radius $r$ at a point $A_1$. Let $B_1$ be the point on the circle such that the line segment $A_1 B_1$ is a diameter of the circle. Let $\alpha+r=5+\sqrt{5}$.
Match each entry in List-I to the correct entry in List-II.
| List-I | List-II |
|---|---|
| (P) $\alpha$ equals | (1) $(-2, 4)$ |
| (Q) $r$ equals | (2) $\sqrt{5}$ |
| (R) $A_1$ equals | (3) $(-2, 6)$ |
| (S) $B_1$ equals | (4) $5$ |
| (5) $(2, 4)$ |
The correct option is
Let $\gamma \in \mathbb{R}$ be such that the lines $L_1: \frac{x+11}{1}=\frac{y+21}{2}=\frac{z+29}{3}$ and $L_2: \frac{x+16}{3}=\frac{y+11}{2}=\frac{z+4}{\gamma}$ intersect. Let $R_1$ be the point of intersection of $L_1$ and $L_2$. Let $O=(0,0,0)$, and $\hat{n}$ denote a unit normal vector to the plane containing both the lines $L_1$ and $L_2$.
Match each entry in List-I to the correct entry in List-II.
| List-I | List-II |
|---|---|
| (P) $\gamma$ equals | (1) $-\hat{i} - \hat{j} + \hat{k}$ |
| (Q) A possible choice for $\hat{n}$ is | (2) $\sqrt{\frac{3}{2}}$ |
| (R) $\overrightarrow{OR_1}$ equals | (3) $1$ |
| (S) A possible value of $\overrightarrow{OR_1} \cdot \hat{n}$ is | (4) $\frac{1}{\sqrt{6}} \hat{i} - \frac{2}{\sqrt{6}} \hat{j} + \frac{1}{\sqrt{6}} \hat{k}$ |
| (5) $\sqrt{\frac{2}{3}}$ |
The correct option is :
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ be functions defined by
$$ f(x)=\left\{\begin{array}{ll} x|x| \sin \left(\frac{1}{x}\right), & x \neq 0, \\ 0, & x=0, \end{array} \quad \text { and } g(x)= \begin{cases}1-2 x, & 0 \leq x \leq \frac{1}{2}, \\ 0, & \text { otherwise } .\end{cases}\right. $$
Let $a, b, c, d \in \mathbb{R}$. Define the function $h: \mathbb{R} \rightarrow \mathbb{R}$ by
$$ h(x)=a f(x)+b\left(g(x)+g\left(\frac{1}{2}-x\right)\right)+c(x-g(x))+d g(x), x \in \mathbb{R} . $$
Match each entry in List-I to the correct entry in List-II.
| List-I | List-II |
|---|---|
| (P) If $a = 0$, $b = 1$, $c = 0$, and $d = 0$, then | (1) $h$ is one-one. |
| (Q) If $a = 1$, $b = 0$, $c = 0$, and $d = 0$, then | (2) $h$ is onto. |
| (R) If $a = 0$, $b = 0$, $c = 1$, and $d = 0$, then | (3) $h$ is differentiable on $\mathbb{R}$. |
| (S) If $a = 0$, $b = 0$, $c = 0$, and $d = 1$, then | (4) the range of $h$ is $[0, 1]$. |
| (5) the range of $h$ is $\{0, 1\}$. |
The correct option is
Physics
A dimensionless quantity is constructed in terms of electronic charge $e$, permittivity of free space $\varepsilon_0$, Planck's constant $h$, and speed of light $c$. If the dimensionless quantity is written as $e^\alpha \varepsilon_0{ }^\beta h^\gamma c^\delta$ and $n$ is a non-zero integer, then $(\alpha, \beta, \gamma, \delta)$ is given by :
An infinitely long wire, located on the $z$-axis, carries a current $I$ along the $+z$-direction and produces the magnetic field $\vec{B}$. The magnitude of the line integral $\int \vec{B} \cdot \overrightarrow{d l}$ along a straight line from the point $(-\sqrt{3} a, a, 0)$ to $(a, a, 0)$ is given by
[ $\mu_0$ is the magnetic permeability of free space.]
Two beads, each with charge $q$ and mass $m$, are on a horizontal, frictionless, non-conducting, circular hoop of radius $a$. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by
[ $\varepsilon_0$ is the permittivity of free space.]
A block of mass $5 \mathrm{~kg}$ moves along the $x$-direction subject to the force $F=(-20 x+10) \mathrm{N}$, with the value of $x$ in metre. At time $t=0 \mathrm{~s}$, it is at rest at position $x=1 \mathrm{~m}$. The position and momentum of the block at $t={\pi \over 4} \mathrm{s}$ are
A particle of mass $m$ is moving in a circular orbit under the influence of the central force $F(r)=-k r$, corresponding to the potential energy $V(r)=k r^2 / 2$, where $k$ is a positive force constant and $r$ is the radial distance from the origin. According to the Bohr's quantization rule, the angular momentum of the particle is given by $L=n \hbar$, where $\hbar=h /(2 \pi), h$ is the Planck's constant, and $n$ a positive integer. If $v$ and $E$ are the speed and total energy of the particle, respectively, then which of the following expression(s) is(are) correct?
Two uniform strings of mass per unit length $\mu$ and $4 \mu$, and length $L$ and $2 L$, respectively, are joined at point $\mathrm{O}$, and tied at two fixed ends $\mathrm{P}$ and $\mathrm{Q}$, as shown in the figure. The strings are under a uniform tension $T$. If we define the frequency $v_0=\frac{1}{2 L} \sqrt{\frac{T}{\mu}}$, which of the following statement(s) is(are) correct?

A glass beaker has a solid, plano-convex base of refractive index 1.60, as shown in the figure. The radius of curvature of the convex surface (SPU) is $9 \mathrm{~cm}$, while the planar surface (STU) acts as a mirror. This beaker is filled with a liquid of refractive index $n$ up to the level QPR. If the image of a point object $\mathrm{O}$ at a height of $h$ (OT in the figure) is formed onto itself, then, which of the following option(s) is(are) correct?

The specific heat capacity of a substance is temperature dependent and is given by the formula $C=k T$, where $k$ is a constant of suitable dimensions in SI units, and $T$ is the absolute temperature. If the heat required to raise the temperature of $1 \mathrm{~kg}$ of the substance from $-73^{\circ} \mathrm{C}$ to $27^{\circ} \mathrm{C}$ is $n k$, the value of $n$ is ________.
[Given: $0 \mathrm{~K}=-273{ }^{\circ} \mathrm{C}$.]



One mole of a monatomic ideal gas undergoes the cyclic process $\mathrm{J} \rightarrow \mathrm{K} \rightarrow \mathrm{L} \rightarrow \mathrm{M} \rightarrow \mathrm{J}$, as shown in the P-T diagram.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
[ $\mathcal{R}$ is the gas constant.]
| List-I | List-II |
|---|---|
| (P) Work done in the complete cyclic process | (1) $RT_0 - 4RT_0 \ln 2$ |
| (Q) Change in the internal energy of the gas in the process JK | (2) $0$ |
| (R) Heat given to the gas in the process KL | (3) $3RT_0$ |
| (S) Change in the internal energy of the gas in the process MJ | (4) $-2RT_0 \ln 2$ |
| (5) $-3RT_0 \ln 2$ |
Four identical thin, square metal sheets, $S_1, S_2, S_3$ and $S_4$, each of side $a$ are kept parallel to each other with equal distance $d(\ll a)$ between them, as shown in the figure. Let $${C_0} = {{{\varepsilon _0}{a^2}} \over d}$$, where $\varepsilon_0$ is the permittivity of free space.
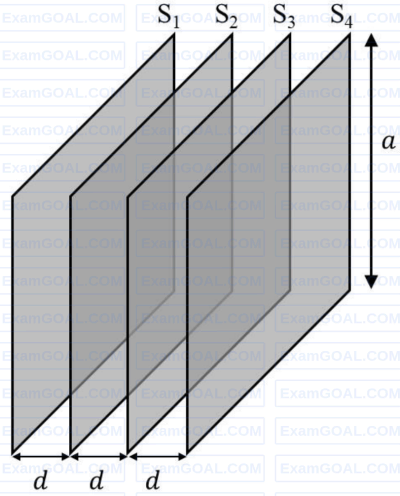
Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) The capacitance between $S_1$ and $S_4$, with $S_2$ and $S_3$ not connected, is | (1) $3C_0$ |
| (Q) The capacitance between $S_1$ and $S_4$, with $S_2$ shorted to $S_3$, is | (2) $\frac{C_0}{2}$ |
| (R) The capacitance between $S_1$ and $S_3$, with $S_2$ shorted to $S_4$, is | (3) $\frac{C_0}{3}$ |
| (S) The capacitance between $S_1$ and $S_2$, with $S_3$ shorted to $S_1$, and $S_2$ shorted to $S_4$, is | (4) $\frac{2C_0}{3}$ |
| (5) $2C_0$ |
A light ray is incident on the surface of a sphere of refractive index $n$ at an angle of incidence $\theta_0$. The ray partially refracts into the sphere with angle of refraction $\phi_0$ and then partly reflects from the back surface. The reflected ray then emerges out of the sphere after a partial refraction. The total angle of deviation of the emergent ray with respect to the incident ray is $\alpha$. Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) If $n = 2$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (1) $30^\circ$ and $0^\circ$ |
| (Q) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (2) $60^\circ$ and $0^\circ$ |
| (R) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\phi_0$ will be | (3) $45^\circ$ and $0^\circ$ |
| (S) If $n = \sqrt{2}$ and $\theta_0 = 45^\circ$, then all the possible values of $\alpha$ will be | (4) $150^\circ$ |
| (5) $0^\circ$ |
The circuit shown in the figure contains an inductor $L$, a capacitor $C_0$, a resistor $R_0$ and an ideal battery. The circuit also contains two keys $\mathrm{K}_1$ and $\mathrm{K}_2$. Initially, both the keys are open and there is no charge on the capacitor. At an instant, key $\mathrm{K}_1$ is closed and immediately after this the current in $R_0$ is found to be $I_1$. After a long time, the current attains a steady state value $I_2$. Thereafter, $\mathrm{K}_2$ is closed and simultaneously $\mathrm{K}_1$ is opened and the voltage across $C_0$ oscillates with amplitude $V_0$ and angular frequency $\omega_0$.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) The value of $I_1$ in Ampere is | (1) $0$ |
| (Q) The value of $I_2$ in Ampere is | (2) $2$ |
| (R) The value of $\omega_0$ in kilo-radians/s is | (3) $4$ |
| (S) The value of $V_0$ in Volt is | (4) $20$ |
| (5) $200$ |