The correct statement(s) related to processes involved in the extraction of metals is(are) :

In the following reactions, $\mathbf{P}, \mathbf{Q}, \mathbf{R}$, and $\mathbf{S}$ are the major products.


The correct statement(s) about $\mathbf{P}, \mathbf{Q}, \mathbf{R}$, and $\mathbf{S}$ is(are) :

Consider the following reaction scheme and choose the correct option(s) for the major products $\mathbf{Q}$, $\mathbf{R}$ and $\mathbf{S}$.

In the scheme given below, $\mathbf{X}$ and $\mathbf{Y}$, respectively, are

Plotting $1 / \Lambda_{\mathrm{m}}$ against $\mathrm{c} \Lambda_{\mathrm{m}}$ for aqueous solutions of a monobasic weak acid $(\mathrm{HX})$ resulted in a straight line with $\mathrm{y}$-axis intercept of $\mathrm{P}$ and slope of $\mathrm{S}$. The ratio $\mathrm{P} / \mathrm{S}$ is

$$ \begin{aligned} & {\left[\Lambda_{\mathrm{m}}=\right.\text { molar conductivity }} \\\\ & \Lambda_{\mathrm{m}}^{\mathrm{o}}=\text { limiting molar conductivity } \\\\ & \mathrm{c}=\text { molar concentration } \\\\ & \left.\mathrm{K}_{\mathrm{a}}=\text { dissociation constant of } \mathrm{HX}\right] \end{aligned} $$

On decreasing the $p \mathrm{H}$ from 7 to 2 , the solubility of a sparingly soluble salt (MX) of a weak acid (HX) increased from $10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}$ to $10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}$. The $p \mathrm{~K}_{\mathrm{a}}$ of $\mathrm{HX}$ is

In the given reaction scheme, $\mathbf{P}$ is a phenyl alkyl ether, $\mathbf{Q}$ is an aromatic compound; $\mathbf{R}$ and $\mathbf{S}$ are the major products.


The correct statement about $\mathbf{S}$ is :

The stoichiometric reaction of $516 \mathrm{~g}$ of dimethyldichlorosilane with water results in a tetrameric cyclic product $\mathbf{X}$ in $75 \%$ yield. The weight (in g) of $\mathbf{X}$ obtained is _______.

[Use, molar mass $\left(\mathrm{g} ~\mathrm{mol}^{-1}\right): \mathrm{H}=1, \mathrm{C}=12, \mathrm{O}=16, \mathrm{Si}=28, \mathrm{Cl}=35.5$ ]

A gas has a compressibility factor of 0.5 and a molar volume of $0.4 ~\mathrm{dm}^3 \mathrm{~mol}^{-1}$ at a temperature of $800 \mathrm{~K}$ and pressure $\mathbf{x}$ atm. If it shows ideal gas behaviour at the same temperature and pressure, the molar volume will be $\mathbf{y} ~\mathrm{dm}^3 \mathrm{~mol}^{-1}$. The value of $\mathbf{x} / \mathbf{y}$ is __________.

[Use: Gas constant, $\mathrm{R}=8 \times 10^{-2} \mathrm{~L}$ atm $\mathrm{K}^{-1} \mathrm{~mol}^{-1}$ ]

The plot of $\log k_f$ versus $1 / T$ for a reversible reaction $\mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g})$ is shown.


Pre-exponential factors for the forward and backward reactions are $10^{15} \mathrm{~s}^{-1}$ and $10^{11} \mathrm{~s}^{-1}$, respectively. If the value of $\log K$ for the reaction at $500 \mathrm{~K}$ is 6 , the value of $\left|\log k_b\right|$ at $250 \mathrm{~K}$ is ______.

$$ \begin{aligned} & {[K=\text { equilibrium constant of the reaction }} \\\\ & k_f=\text { rate constant of forward reaction } \\\\ & \left.k_b=\text { rate constant of backward reaction }\right] \end{aligned} $$

One mole of an ideal monoatomic gas undergoes two reversible processes $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ as shown in the given figure:


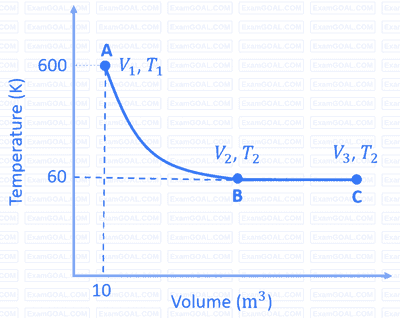
$\mathrm{A} \rightarrow \mathrm{B}$ is an adiabatic process. If the total heat absorbed in the entire process $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ is $\mathrm{R} T_2 \ln 10$, the value of $2 \log V_3$ is _______.

[Use, molar heat capacity of the gas at constant pressure, $C_{\mathrm{p}, \mathrm{m}}=\frac{5}{2} \mathrm{R}$ ]

In a one-litre flask, 6 moles of $A$ undergoes the reaction $A(\mathrm{~g}) \rightleftharpoons P(\mathrm{~g})$. The progress of product formation at two temperatures (in Kelvin), $\mathrm{T}_1$ and $\mathrm{T}_2$, is shown in the figure:


If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.

$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]

The total number of $s p^2$ hybridised carbon atoms in the major product $\mathbf{P}$ (a non-heterocyclic compound) of the following reaction is ______.

Match the reactions (in the given stoichiometry of the reactants) in List-I with one of their products given in List-II and choose the correct option.

List - I	List - II
(P) $\mathrm{P}_2 \mathrm{O}_3+3 \mathrm{H}_2 \mathrm{O} \rightarrow$	(1) $\mathrm{P}(\mathrm{O})\left(\mathrm{OCH}_3\right) \mathrm{Cl}_2$
(Q) $\mathrm{P}_4+3 \mathrm{NaOH}+3 \mathrm{H}_2 \mathrm{O} \rightarrow$	(2) $\mathrm{H}_3 \mathrm{PO}_3$
(R) $\mathrm{PCl}_5+\mathrm{CH}_3 \mathrm{COOH} \rightarrow$	(3) $\mathrm{PH}_3$
(S) $\mathrm{H}_3 \mathrm{PO}_2+2 \mathrm{H}_2 \mathrm{O}+4 \mathrm{AgNO}_3 \rightarrow$	(4) $\mathrm{POCl}_3$
	(5) $\mathrm{H}_3 \mathrm{PO}_4$

Match the electronic configurations in List-I with appropriate metal complex ions in List-II and choose the correct option.

[Atomic Number: $\mathrm{Fe}=26, \mathrm{Mn}=25, \mathrm{Co}=27$ ]

List - I	List - II
(P) $t_{2 g}^6 e_g^0$	(1) $\left[\mathrm{Fe}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}$
(Q) $t_{2 g}^3 e_g^2$	(2) $\left[\mathrm{Mn}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}$
(R) $\mathrm{e}^2 \mathrm{t}_2^3$	(3) $\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_6\right]^{3+}$
(S) $t_{2 g}^4 e_g^2$	(4) $\left[\mathrm{FeCl}_4\right]^{-}$
	(5) $\left[\mathrm{CoCl}_4\right]^{2-}$

Match the reactions in List-I with the features of their products in List-II and choose the correct option.

List - I	List - II
(P)	(1) Inversion of configuration
(Q)	(2) Retention of configuration
(R)	(3) Mixture of enantiomers
(S)	(4) Mixture of structural isomers
	(5) Mixture of diastereomers

The major products obtained from the reactions in List-II are the reactants for the named reactions mentioned in List-I. Match List-I with List-II and choose the correct option.

List - I	List - II
(P) Etard reaction	(1) Acetophenone $\stackrel{\mathrm{Zn}-\mathrm{Hg}, \mathrm{HCl}}{\longrightarrow}$
(Q) Gattermann reaction	(2) $$ \text { Toluene } \underset{\text { (ii) } \mathrm{SOCl}_2}{\stackrel{\text { (i) } \mathrm{KMnO}_4, \mathrm{KOH}, \Delta}{\longrightarrow}} $$
(R) Gattermann-Koch reaction	(3) $$ \text { Benzene } \underset{\text { anhyd. } \mathrm{AlCl}_3}{\stackrel{\mathrm{CH}_3 \mathrm{Cl}}{\longrightarrow}} $$
(S) Rosenmund reduction	(4) $$ \text { Aniline } \underset{273-278 \mathrm{~K}}{\stackrel{\mathrm{NaNO}_2 / \mathrm{HCl}}{\longrightarrow}} $$
	(5) $$ \text { Phenol } \stackrel{\mathrm{Zn}, \Delta}{\longrightarrow} $$

Let $S=(0,1) \cup(1,2) \cup(3,4)$ and $T=\{0,1,2,3\}$. Then which of the following statements is(are) true?

Let $T_1$ and $T_2$ be two distinct common tangents to the ellipse $E: \frac{x^2}{6}+\frac{y^2}{3}=1$ and the parabola $P: y^2=12 x$. Suppose that the tangent $T_1$ touches $P$ and $E$ at the points $A_1$ and $A_2$, respectively and the tangent $T_2$ touches $P$ and $E$ at the points $A_4$ and $A_3$, respectively. Then which of the following statements is(are) true?

Let $f:[0,1] \rightarrow[0,1]$ be the function defined by $f(x)=\frac{x^3}{3}-x^2+\frac{5}{9} x+\frac{17}{36}$. Consider the square region $S=[0,1] \times[0,1]$. Let $G=\{(x, y) \in S: y>f(x)\}$ be called the green region and $R=\{(x, y) \in S: y < f(x)\}$ be called the red region. Let $L_h=\{(x, h) \in S: x \in[0,1]\}$ be the horizontal line drawn at a height $h \in[0,1]$. Then which of the following statements is(are) true?

Let $f:(0,1) \rightarrow \mathbb{R}$ be the function defined as $f(x)=\sqrt{n}$ if $x \in\left[\frac{1}{n+1}, \frac{1}{n}\right)$ where $n \in \mathbb{N}$. Let $g:(0,1) \rightarrow \mathbb{R}$ be a function such that $\int\limits_{x^2}^x \sqrt{\frac{1-t}{t}} d t < g(x) < 2 \sqrt{x}$ for all $x \in(0,1)$. Then $\lim\limits_{x \rightarrow 0} f(x) g(x)$

Let $Q$ be the cube with the set of vertices $\left\{\left(x_1, x_2, x_3\right) \in \mathbb{R}^3: x_1, x_2, x_3 \in\{0,1\}\right\}$. Let $F$ be the set of all twelve lines containing the diagonals of the six faces of the cube $Q$. Let $S$ be the set of all four lines containing the main diagonals of the cube $Q$; for instance, the line passing through the vertices $(0,0,0)$ and $(1,1,1)$ is in $S$. For lines $\ell_1$ and $\ell_2$, let $d\left(\ell_1, \ell_2\right)$ denote the shortest distance between them. Then the maximum value of $d\left(\ell_1, \ell_2\right)$, as $\ell_1$ varies over $F$ and $\ell_2$ varies over $S$, is :

Let $X=\left\{(x, y) \in \mathbb{Z} \times \mathbb{Z}: \frac{x^2}{8}+\frac{y^2}{20}<1\right.$ and $\left.y^2<5 x\right\}$. Three distinct points $P, Q$ and $R$ are randomly chosen from $X$. Then the probability that $P, Q$ and $R$ form a triangle whose area is a positive integer, is :

Let $P$ be a point on the parabola $y^2=4 a x$, where $a>0$. The normal to the parabola at $P$ meets the $x$-axis at a point $Q$. The area of the triangle $P F Q$, where $F$ is the focus of the parabola, is 120 . If the slope $m$ of the normal and $a$ are both positive integers, then the pair $(a, m)$ is

Let $\tan ^{-1}(x) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, for $x \in \mathbb{R}$. Then the number of real solutions of the equation $\sqrt{1+\cos (2 x)}=\sqrt{2} \tan ^{-1}(\tan x)$ in the set $\left(-\frac{3 \pi}{2},-\frac{\pi}{2}\right) \cup\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)$ is equal to :

Let $n \geq 2$ be a natural number and $f:[0,1] \rightarrow \mathbb{R}$ be the function defined by

$$ f(x)= \begin{cases}n(1-2 n x) & \text { if } 0 \leq x \leq \frac{1}{2 n} \\\\ 2 n(2 n x-1) & \text { if } \frac{1}{2 n} \leq x \leq \frac{3}{4 n} \\\\ 4 n(1-n x) & \text { if } \frac{3}{4 n} \leq x \leq \frac{1}{n} \\\\ \frac{n}{n-1}(n x-1) & \text { if } \frac{1}{n} \leq x \leq 1\end{cases} $$

If $n$ is such that the area of the region bounded by the curves $x=0, x=1, y=0$ and $y=f(x)$ is 4 , then the maximum value of the function $f$ is :

Let $7 \overbrace{5 \cdots 5}^r 7$ denote the $(r+2)$ digit number where the first and the last digits are 7 and the remaining $r$ digits are 5 . Consider the sum $S=77+757+7557+\cdots+7 \overbrace{5 \cdots 5}^{98}7$. If $S=\frac{7 \overbrace{5 \cdots 5}^{99}7+m}{n}$, where $m$ and $n$ are natural numbers less than 3000 , then the value of $m+n$ is

Let $A=\left\{\frac{1967+1686 i \sin \theta}{7-3 i \cos \theta}: \theta \in \mathbb{R}\right\}$. If $A$ contains exactly one positive integer $n$, then the value of $n$ is

Let $P$ be the plane $\sqrt{3} x+2 y+3 z=16$ and let $S=\left\{\alpha \hat{i}+\beta \hat{j}+\gamma \hat{k}: \alpha^2+\beta^2+\gamma^2=1\right.$ and the distance of $(\alpha, \beta, \gamma)$ from the plane $P$ is $\left.\frac{7}{2}\right\}$. Let $\vec{u}, \vec{v}$ and $\vec{w}$ be three distinct vectors in $S$ such that $|\vec{u}-\vec{v}|=|\vec{v}-\vec{w}|=|\vec{w}-\vec{u}|$. Let $V$ be the volume of the parallelepiped determined by vectors $\vec{u}, \vec{v}$ and $\vec{w}$. Then the value of $\frac{80}{\sqrt{3}} V$ is :

Let $a$ and $b$ be two nonzero real numbers. If the coefficient of $x^5$ in the expansion of $\left(a x^2+\frac{70}{27 b x}\right)^4$ is equal to the coefficient of $x^{-5}$ in the expansion of $\left(a x-\frac{1}{b x^2}\right)^7$, then the value of $2 b$ is :

Let $\alpha, \beta$ and $\gamma$ be real numbers. Consider the following system of linear equations

$$ \begin{aligned} & x+2 y+z=7 \\\\ & x+\alpha z=11 \\\\ & 2 x-3 y+\beta z=\gamma \end{aligned} $$

Match each entry in List-I to the correct entries in List-II.

List - I	List - II
(P) If $\beta=\frac{1}{2}(7 \alpha-3)$ and $\gamma=28$, then the system has	(1) a unique solution
(Q) If $\beta=\frac{1}{2}(7 \alpha-3)$ and $\gamma \neq 28$, then the system has	(2) no solution
(R) If $\beta \neq \frac{1}{2}(7 \alpha-3)$ where $\alpha=1$ and $\gamma \neq 28$, then the system has	(3) infinitely many solutions
(S) If $\beta \neq \frac{1}{2}(7 \alpha-3)$ where $\alpha=1$ and $\gamma=28$, then the system has	(4) $x=11, y=-2$ and $z=0$ as a solution
	(5) $x=-15, y=4$ and $z=0$ as a solution

The correct option is:

Consider the given data with frequency distribution

$$ \begin{array}{ccccccc} x_i & 3 & 8 & 11 & 10 & 5 & 4 \\ f_i & 5 & 2 & 3 & 2 & 4 & 4 \end{array} $$

Match each entry in List-I to the correct entries in List-II.

List - I	List - II
(P) The mean of the above data is	(1) 2.5
(Q) The median of the above data is	(2) 5
(R) The mean deviation about the mean of the above data is	(3) 6
(S) The mean deviation about the median of the above data is	(4) 2.7
	(5) 2.4

The correct option is:

Let $\ell_1$ and $\ell_2$ be the lines $\vec{r}_1=\lambda(\hat{i}+\hat{j}+\hat{k})$ and $\vec{r}_2=(\hat{j}-\hat{k})+\mu(\hat{i}+\hat{k})$, respectively. Let $X$ be the set of all the planes $H$ that contain the line $\ell_1$. For a plane $H$, let $d(H)$ denote the smallest possible distance between the points of $\ell_2$ and $H$. Let $H_0$ be a plane in $X$ for which $d\left(H_0\right)$ is the maximum value of $d(H)$ as $H$ varies over all planes in $X$.

Match each entry in List-I to the correct entries in List-II.

List - I	List - II
(P) The value of $d\left(H_0\right)$ is	(1) $\sqrt{3}$
(Q) The distance of the point $(0,1,2)$ from $H_0$ is	(2) $\frac{1}{\sqrt{3}}$
(R) The distance of origin from $H_0$ is	(3) 0
(S) The distance of origin from the point of intersection of planes $y=z, x=1$ and $H_0$ is	(4) $\sqrt{2}$
	(5) $\frac{1}{\sqrt{2}}$

The correct option is:

Let $z$ be a complex number satisfying $|z|^3+2 z^2+4 \bar{z}-8=0$, where $\bar{z}$ denotes the complex conjugate of $z$. Let the imaginary part of $z$ be nonzero.

Match each entry in List-I to the correct entries in List-II.

List - I	List - II
(P) $|z|^2$ is equal to	(1) 12
(Q) $|z-\bar{z}|^2$ is equal to	(2) 4
(R) $|z|^2+|z+\bar{z}|^2$ is equal to	(3) 8
(S) $|z+1|^2$ is equal to	(4) 10
	(5) 7

The correct option is:

A slide with a frictionless curved surface, which becomes horizontal at its lower end, is fixed on the terrace of a building of height $3 h$ from the ground, as shown in the figure. A spherical ball of mass $m$ is released on the slide from rest at a height $h$ from the top of the terrace. The ball leaves the slide with a velocity $\vec{u}_0=u_0 \hat{x}$ and falls on the ground at a distance $d$ from the building making an angle $\theta$ with the horizontal. It bounces off with a velocity $\vec{v}$ and reaches a maximum height $h_1$. The acceleration due to gravity is $g$ and the coefficient of restitution of the ground is $1 / \sqrt{3}$. Which of the following statement(s) is(are) correct?

A plane polarized blue light ray is incident on a prism such that there is no reflection from the surface of the prism. The angle of deviation of the emergent ray is $\delta=60^{\circ}$ (see Figure-1). The angle of minimum deviation for red light from the same prism is $\delta_{\min }=30^{\circ}$ (see Figure-2). The refractive index of the prism material for blue light is $\sqrt{3}$. Which of the following statement(s) is(are) correct?

In a circuit shown in the figure, the capacitor $C$ is initially uncharged and the key $K$ is open. In this condition, a current of $1 \mathrm{~A}$ flows through the $1 \Omega$ resistor. The key is closed at time $t=t_0$. Which of the following statement(s) is(are) correct?

[Given: $e^{-1}=0.36$ ]

A bar of mass $M=1.00 \mathrm{~kg}$ and length $L=0.20 \mathrm{~m}$ is lying on a horizontal frictionless surface. One end of the bar is pivoted at a point about which it is free to rotate. A small mass $m=0.10 \mathrm{~kg}$ is moving on the same horizontal surface with $5.00 \mathrm{~m} \mathrm{~s}^{-1}$ speed on a path perpendicular to the bar. It hits the bar at a distance $L / 2$ from the pivoted end and returns back on the same path with speed v. After this elastic collision, the bar rotates with an angular velocity $\omega$.

Which of the following statement is correct?

A container has a base of $50 \mathrm{~cm} \times 5 \mathrm{~cm}$ and height $50 \mathrm{~cm}$, as shown in the figure. It has two parallel electrically conducting walls each of area $50 \mathrm{~cm} \times 50 \mathrm{~cm}$. The remaining walls of the container are thin and non-conducting. The container is being filled with a liquid of dielectric constant 3 at a uniform rate of $250 \mathrm{~cm}^3 \mathrm{~s}^{-1}$. What is the value of the capacitance of the container after 10 seconds?

[Given: Permittivity of free space $\epsilon_0=9 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}$, the effects of the non-conducting walls on the capacitance are negligible]

One mole of an ideal gas expands adiabatically from an initial state $\left(T_{\mathrm{A}}, V_0\right)$ to final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. Another mole of the same gas expands isothermally from a different initial state $\left(T_{\mathrm{B}}, V_0\right)$ to the same final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. The ratio of the specific heats at constant pressure and constant volume of this ideal gas is $\gamma$. What is the ratio $T_{\mathrm{A}} / T_{\mathrm{B}}$ ?

Two satellites $\mathrm{P}$ and $\mathrm{Q}$ are moving in different circular orbits around the Earth (radius $R$ ). The heights of $\mathrm{P}$ and $\mathrm{Q}$ from the Earth surface are $h_{\mathrm{P}}$ and $h_{\mathrm{Q}}$, respectively, where $h_{\mathrm{P}}=R / 3$. The accelerations of $\mathrm{P}$ and $\mathrm{Q}$ due to Earth's gravity are $g_{\mathrm{P}}$ and $g_{\mathrm{Q}}$, respectively. If $g_{\mathrm{P}} / g_{\mathrm{Q}}=36 / 25$, what is the value of $h_{\mathrm{Q}}$ ?

A Hydrogen-like atom has atomic number $Z$. Photons emitted in the electronic transitions from level $n=4$ to level $n=3$ in these atoms are used to perform photoelectric effect experiment on a target metal. The maximum kinetic energy of the photoelectrons generated is $1.95 \mathrm{eV}$. If the photoelectric threshold wavelength for the target metal is $310 \mathrm{~nm}$, the value of $Z$ is _________.

[Given: $h c=1240 \mathrm{eV}-\mathrm{nm}$ and $R h c=13.6 \mathrm{eV}$, where $R$ is the Rydberg constant, $h$ is the Planck's constant and $c$ is the speed of light in vacuum]

An optical arrangement consists of two concave mirrors $M_1$ and $M_2$, and a convex lens $L$ with a common principal axis, as shown in the figure. The focal length of $\mathrm{L}$ is $10 \mathrm{~cm}$. The radii of curvature of $M_1$ and $M_2$ are $20 \mathrm{~cm}$ and $24 \mathrm{~cm}$, respectively. The distance between $L$ and $M_2$ is $20 \mathrm{~cm}$. A point object $S$ is placed at the mid-point between $\mathrm{L}$ and $M_2$ on the axis. When the distance between $\mathrm{L}$ and $\mathrm{M}_1$ is $n / 7 \mathrm{~cm}$, one of the images coincides with $\mathrm{S}$. The value of $n$ is _______.

In an experiment for determination of the focal length of a thin convex lens, the distance of the object from the lens is $10 \pm 0.1 \mathrm{~cm}$ and the distance of its real image from the lens is $20 \pm 0.2 \mathrm{~cm}$. The error in the determination of focal length of the lens is $n \%$. The value of $n$ is ______.

A closed container contains a homogeneous mixture of two moles of an ideal monatomic gas $(\gamma=5 / 3)$ and one mole of an ideal diatomic gas $(\gamma=7 / 5)$. Here, $\gamma$ is the ratio of the specific heats at constant pressure and constant volume of an ideal gas. The gas mixture does a work of 66 Joule when heated at constant pressure. The change in its internal energy is _______ Joule.

A person of height $1.6 \mathrm{~m}$ is walking away from a lamp post of height $4 \mathrm{~m}$ along a straight path on the flat ground. The lamp post and the person are always perpendicular to the ground. If the speed of the person is $60 \mathrm{~cm} \mathrm{~s}^{-1}$, the speed of the tip of the person's shadow on the ground with respect to the person is ____________ $\mathrm{cm}~ \mathrm{s}^{-1}$.

Two point-like objects of masses $20 ~\mathrm{gm}$ and $30 ~\mathrm{gm}$ are fixed at the two ends of a rigid massless rod of length $10 \mathrm{~cm}$. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is $1.2 \times 10^{-8} \mathrm{~N} \mathrm{~m} ~\mathrm{rad}^{-1}$. The angular frequency of the oscillations in $n \times 10^{-3} ~\mathrm{rad} ~\mathrm{s}^{-1}$. The value of $n$ is _________ .

List-I shows different radioactive decay processes and List-II provides possible emitted particles. Match each entry in List-I with an appropriate entry from List-II, and choose the correct option.

List - I	List - II
(P) ${ }_{92}^{238} U \rightarrow{ }_{91}^{234} \mathrm{~Pa}$	(1) one $\alpha$ particle and one $\beta^{+}$particle
(Q) ${ }_{82}^{214} \mathrm{~Pb} \rightarrow{ }_{82}^{210} \mathrm{~Pb}$	(2) three $\beta^{-}$particles and one $\alpha$ particle
(R) ${ }_{81}^{210} \mathrm{Tl} \rightarrow{ }_{82}^{206} \mathrm{~Pb}$	(3) two $\beta^{-}$particles and one $\alpha$ particle
(S) ${ }_{91}^{228} \mathrm{~Pa} \rightarrow{ }_{88}^{224} \mathrm{Ra}$	(4) one $\alpha$ particle and one $\beta^{-}$particle
	(5) one $\alpha$ particle and two $\beta^{+}$particles

Match the temperature of a black body given in List-I with an appropriate statement in List-II, and choose the correct option.

[Given: Wien's constant as $2.9 \times 10^{-3} \mathrm{~m}-\mathrm{K}$ and $\frac{h c}{e}=1.24 \times 10^{-6} \mathrm{~V}-\mathrm{m}$ ]

List - I	List - II
(P) $2000 \mathrm{~K}$	(1) The radiation at peak wavelength can lead to emission of photoelectrons from a metal of work function $4 \mathrm{eV}$.
(Q) $3000 \mathrm{~K}$	(2) The radiation at peak wavelength is visible to human eye.
(R) $5000 \mathrm{~K}$	(3) The radiation at peak emission wavelength will result in the widest central maximum of a single slit diffraction.
(S) $10000 \mathrm{~K}$	(4) The power emitted per unit area is $1 / 16$ of that emitted by a blackbody at temperature $6000 \mathrm{~K}$.
	(5) The radiation at peak emission wavelength can be used to image human bones.

A series LCR circuit is connected to a $45 \sin (\omega t)$ Volt source. The resonant angular frequency of the circuit is $10^5 ~\mathrm{rad}~ \mathrm{s}^{-1}$ and current amplitude at resonance is $I_0$. When the angular frequency of the source is $\omega=8 \times 10^4 ~\mathrm{rad} ~\mathrm{s}^{-1}$, the current amplitude in the circuit is $0.05 I_0$. If $L=50 ~\mathrm{mH}$, match each entry in List-I with an appropriate value from List-II and choose the correct option.

List - I	List - II
(P) $I_0$ in $\mathrm{mA}$	(1) 44.4
(Q) The quality factor of the circuit	(2) 18
(R) The bandwidth of the circuit in $\mathrm{rad}~ \mathrm{s}^{-1}$	(3) 400
(S) The peak power dissipated at resonance in Watt	(4) 2250
	(5) 500

A thin conducting rod $M N$ of mass $20 ~\mathrm{gm}$, length $25 \mathrm{~cm}$ and resistance $10 ~\Omega$ is held on frictionless, long, perfectly conducting vertical rails as shown in the figure. There is a uniform magnetic field $B_0=4 \mathrm{~T}$ directed perpendicular to the plane of the rod-rail arrangement. The rod is released from rest at time $t=0$ and it moves down along the rails. Assume air drag is negligible. Match each quantity in List-I with an appropriate value from List-II, and choose the correct option.

[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ and $e^{-1}=0.4$ ]

List - I	List - II
(P) At $t=0.2 \mathrm{~s}$, the magnitude of the induced emf in Volt	(1) 0.07
(Q) At $t=0.2 \mathrm{~s}$, the magnitude of the magnetic force in Newton	(2) 0.14
(R) At $t=0.2 \mathrm{~s}$, the power dissipated as heat in Watt	(3) 1.20
(S) The magnitude of terminal velocity of the rod in $\mathrm{m} \mathrm{s}^{-1}$	(4) 0.12
	(5) 2.00