Bombardment of aluminium by $$\alpha$$-particle leads to its artificial disintegration in two ways : (i) and (ii) as shown. Products X, Y and Z, respectively, are

AgNO₃(aq.) was added to an aqueous KCl solution gradually and the conductivity of the solution was measured. The plot of conductance ($$\Lambda $$) versus the volume of AgNO₃ is

The major product of the following reaction is

Extra very pure N₂ can be obtained by heating

Among the given options, the compound(s) in which all the atoms are in one plane in all the possible conformations (if any) is(are)

The structure of compound P is

The structure of the compound Q is

The compound N is

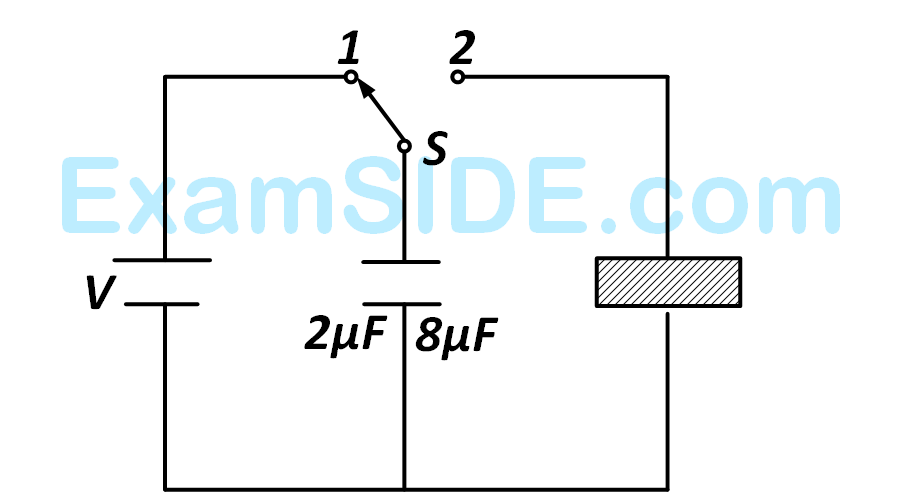
The final solution contains :

Reaction of Br₂ with Na₂CO₃ in aqueous solution gives sodium bromide and sodium bromate with evolution of CO₂ gas. The number of sodium bromide molecules involved in the balanced chemical equation is ________.

The total number of alkenes possible by dehydrobromination of 3-bromo-3-cyclopentylhexane using alcoholic KOH is _______.

A decapeptide (mol. wt. 796) on complete hydrolysis gives glycine (mol. wt. 75), alanine and phenylalanine. Glycine contributes 47.0% to the total weight of the hydrolysed products. The number of glycine units present in the decapeptide is _________.

The probability of the drawn ball from $${U_2}$$ being white is

Given that the drawn ball from $${U_2}$$ is white, the probability that head appeared on the coin is

Then the value of $${d \over {d\left( {\tan \theta } \right)}}\left( {f\left( \theta \right)} \right)$$ is

Let $$P = \{ \theta :\sin \theta - \cos \theta = \sqrt 2 \cos \theta \} $$ and $$Q = \{ \theta :\sin \theta + \cos \theta = \sqrt 2 \sin \theta \} $$ be two sets. Then

Let f : R $$\to$$ R be a function such that $$f(x + y) = f(x) + f(y),\,\forall x,y \in R$$. If f(x) is differentiable at x = 0, then

Let M and N be two 3 $$\times$$ 3 non-singular skew symmetric matrices such that MN = NM. If P^T denotes the transpose of P, then M²N²(M^TN)^$$-$$1(MN^$$-$$1)^T is equal to

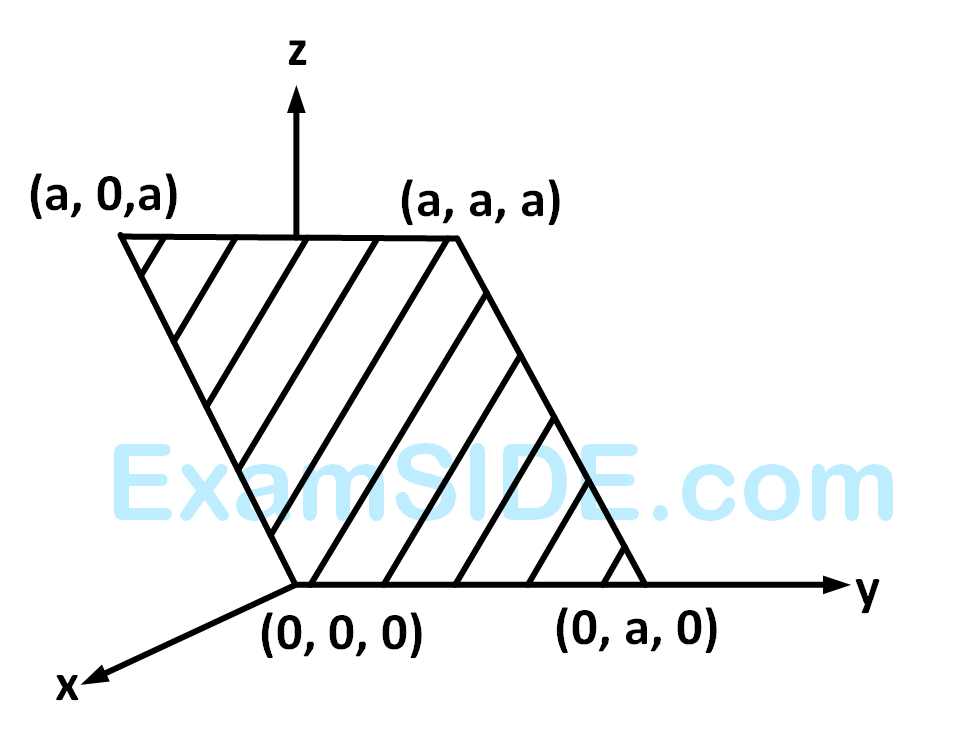
If the point P(a, b, c), with reference to (E), lies on the plane 2x + y + z = 1, then the value of 7a + b + c is

Let $$\omega$$ be a solution of $${x^3} - 1 = 0$$ with $${\mathop{\rm Im}\nolimits} (\omega ) > 0$$. If a = 2 with b and c satisfying (E), then the value of $${3 \over {{\omega ^a}}} + {1 \over {{\omega ^b}}} + {3 \over {{\omega ^c}}}$$ is equal to

Let b = 6, with a and c satisfying (E). If $$\alpha$$ and $$\beta$$ are the roots of the quadratic equation ax² + bx + c = 0, then $$\sum\limits_{n = 0}^\infty {{{\left( {{1 \over \alpha } + {1 \over \beta }} \right)}^n}} $$ is

Let $$f:[1,\infty ) \to [2,\infty )$$ be a differentiable function such that $$f(1) = 2$$. If $$6\int\limits_1^x {f(t)dt = 3xf(x) - {x^3} - 5} $$ for all $$x \ge 1$$, then the value of f(2) is ___________.

Taking the electronic charge as 'e' and the permittivity as $$'{\varepsilon _0}'$$. Use dimensional analysis to determine the correct expression for $${\omega _p}$$.

Estimate the wavelength at which plasma reflection will occur for a metal having the density of electrons N $$ \approx $$ 4 $$ \times $$ 10²⁷ m^-3. Taking $${{\varepsilon _0}}$$ = 10^{- 11} and m $$ \approx $$ 10^{- 30}, where these quantities are in proper SI units.

A ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in radian/s) is

Four solid spheres each of diameter $$\sqrt 5 $$ cm and mass 0.5 kg are placed with their centers at the corners of a square of side 4 cm. The moment of inertia of the system about the diagonal of the square is N $$ \times $$ 10⁻⁴ kg-m², then N is

The wavelength of the first spectral line in the Balmer series of hydrogen atom is 6561 $$\mathop A\limits^o $$. The wavelength of the second spectral line in the Balmer series of singly-ionized helium atom is

A meter bridge is set up as shown, to determine an unknown resistance X using a standard 10 $$\Omega$$ resistor. The galvanometer shows null point when tapping-key is at 52 cm mark. The end-corrections are 1 cm and 2 cm, respectively, for the ends A and B. The determined value of X is

A metal rod of length L and mass m is pivoted at one end. A thin disk of mass M and radius R ( < L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached : (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its centre. The rod-disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is(are) true?

A composite block is made of slabs A, B, C, D and E of different thermal conductivities (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat Q flows only from left to right through the blocks. Then, in steady-state

An electron and a proton are moving on straight parallel paths with same velocity. They enter a semi-infinite region of uniform magnetic field perpendicular to the velocity. Which of the following statement(s) is/are true?

The phase space diagram for a ball thrown vertically up from ground is

The phase space diagram for simple harmonic motion is a circle centred at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and E₁ and E₂ are the total mechanical energies respectively. Then

Consider the spring-mass system, with the mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is

A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2 N on the ring and rolls it without slipping with an acceleration of 0.2 m/s². The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is (P/10). The value of P is _________.

Four point charges, each of +q, are rigidly fixed at the four corners of a square planar soap film of side a. The surface tension of the soap film is $$\gamma$$. The system of charges and planar film are in equilibrium, and $$a = k{\left[ {{{{q^2}} \over \gamma }} \right]^{1/N}}$$, where k is a constant. Then N is __________.

The activity of a freshly prepared radioactive sample is 10¹⁰ disintegrations per second, whose mean life is 10⁹ s. The mass of an atom of this radioisotope is 10^$$-$$25 kg. The mass (in mg) of the radioactive sample is _________.

A long circular tube of length 10 m and radius 0.3 m carries a current I along its curved surface as shown. A wire-loop of resistance 0.005 $$\Omega$$ and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $$I = {I_0}\cos (300t)$$, where I₀ is constant. If the magnetic moment of the loop is $$N{\mu _0}{I_0}\sin (300t)$$, then N is ___________.