Chemistry
During sodium nitroprusside test of sulphide ion in an aqueous solution, one of the ligands coordinated to the metal ion is converted to
The complete hydrolysis of ICl, ClF3 and BrF5, respectively, gives :
Monocyclic compounds $\mathbf{P}, \mathbf{Q}, \mathbf{R}$ and $\mathbf{S}$ are the major products formed in the reaction sequences given below.


The product having the highest number of unsaturated carbon atom(s) is :
The correct statement(s) about intermolecular forces is(are)
The compound(s) with P–H bond(s) is(are)
For the reaction sequence given below, the correct statement(s) is(are):

For the reaction sequence given below, the correct statement(s) is(are)

The density (in $\mathrm{g} \mathrm{cm}^{-3}$ ) of the metal which forms a cubic close packed (ccp) lattice with an axial distance (edge length) equal to 400 pm is ___________.
Use: Atomic mass of metal $=105.6 \mathrm{amu}$ and Avogadro's constant $=6 \times 10^{23} \mathrm{~mol}^{-1}$
The solubility of barium iodate in an aqueous solution prepared by mixing 200 mL of 0.010 M barium nitrate with 100 mL of 0.10 M sodium iodate is $\boldsymbol{X} \times 10^{-6} \mathrm{~mol} \mathrm{dm}^{-3}$. The value of $\boldsymbol{X}$ is ____________.
Use: Solubility product constant $\left(K_{\mathrm{sp}}\right)$ of barium iodate $=1.58 \times 10^{-9}$
Adsorption of phenol from its aqueous solution on to fly ash obeys Freundlich isotherm. At a given temperature, from $10 \mathrm{mg} \mathrm{g}^{-1}$ and $16 \mathrm{mg} \mathrm{g}^{-1}$ aqueous phenol solutions, the concentrations of adsorbed phenol are measured to be $4 \mathrm{mg} \mathrm{g}^{-1}$ and $10 \mathrm{mg} \mathrm{g}^{-1}$, respectively. At this temperature, the concentration (in $\mathrm{mg} \mathrm{g}^{-1}$ ) of adsorbed phenol from $20 \mathrm{mg} \mathrm{g}^{-1}$ aqueous solution of phenol will be ______________.
Use: $\log _{10} 2=0.3$
Consider a reaction $A+R \rightarrow$ Product. The rate of this reaction is measured to be $k[A][R]$. At the start of the reaction, the concentration of $R,[R]_0$, is 10-times the concentration of $A,[A]_0$. The reaction can be considered to be a pseudo first order reaction with assumption that $k[R]=k^{\prime}$ is constant. Due to this assumption, the relative error (in %) in the rate when this reaction is $40 \%$ complete, is ___________.
[ $k$ and $k^{\prime}$ represent corresponding rate constants]
At 300 K , an ideal dilute solution of a macromolecule exerts osmotic pressure that is expressed in terms of the height $(h)$ of the solution (density $=1.00 \mathrm{~g} \mathrm{~cm}^{-3}$ ) where $h$ is equal to 2.00 cm . If the concentration of the dilute solution of the macromolecule is $2.00 \mathrm{~g} \mathrm{dm}^{-3}$, the molar mass of the macromolecule is calculated to be $\boldsymbol{X} \times 10^4 \mathrm{~g} \mathrm{~mol}^{-1}$. The value of $\boldsymbol{X}$ is __________.
Use: Universal gas constant $(R)=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$ and acceleration due to gravity $(g)=10 \mathrm{~m} \mathrm{~s}^{-2}$
An electrochemical cell is fueled by the combustion of butane at 1 bar and 298 K . Its cell potential is $\frac{\boldsymbol{X}}{F} \times 10^3$ volts, where $F$ is the Faraday constant. The value of $\boldsymbol{X}$ is _____________.
Use: Standard Gibbs energies of formation at 298 K are: $\Delta_f G_{\mathrm{CO}_2}^o=-394 \mathrm{~kJ} \mathrm{~mol}^{-1} ; \Delta_f G_{\text {water }}^o=$ $-237 \mathrm{~kJ} \mathrm{~mol}^{-1} ; \Delta_f G_{\text {butane }}^o=-18 \mathrm{~kJ} \mathrm{~mol}^{-1}$
A linear octasaccharide (molar mass $=1024 \mathrm{~g} \mathrm{~mol}^{-1}$ ) on complete hydrolysis produces three monosaccharides: ribose, 2-deoxyribose and glucose. The amount of 2-deoxyribose formed is $58.26 \%(\mathrm{w} / \mathrm{w})$ of the total amount of the monosaccharides produced in the hydrolyzed products. The number of ribose unit(s) present in one molecule of octasaccharide is $\qquad$ .
Use: Molar mass $\left(\right.$ in g $\left.\mathrm{mol}^{-1}\right)$ : ribose $=150,2$-deoxyribose $=134$, glucose $=180$;
Atomic mass (in amu): $\mathrm{H}=1, \mathrm{O}=16$
Mathematics
Let $x_0$ be the real number such that $e^{x_0} + x_0 = 0$. For a given real number $\alpha$, define
$$g(x) = \frac{3x e^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)}$$
for all real numbers $x$.
Then which one of the following statements is TRUE?
Let ℝ denote the set of all real numbers. Then the area of the region
$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x}, 5x - 4y - 1 > 0, 4x + 4y - 17 < 0 \right\} $
is
The total number of real solutions of the equation
$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1}\left(\frac{6 \tan \theta}{9 + \tan^2 \theta}\right) $
is
(Here, the inverse trigonometric functions $\sin^{-1} x$ and $\tan^{-1} x$ assume values in $[ -\frac{\pi}{2}, \frac{\pi}{2}]$ and $( -\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)
Let S denote the locus of the point of intersection of the pair of lines
$4x - 3y = 12\alpha$,
$4\alpha x + 3\alpha y = 12$,
where $\alpha$ varies over the set of non-zero real numbers. Let T be the tangent to S passing through the points $(p, 0)$ and $(0, q)$, $q > 0$, and parallel to the line $4x - \frac{3}{\sqrt{2}} y = 0$.
Then the value of $pq$ is :
Then which of the following statements is (are) TRUE?
Let $S$ denote the locus of the mid-points of those chords of the parabola $y^2=x$, such that the area of the region enclosed between the parabola and the chord is $\frac{4}{3}$. Let $\mathcal{R}$ denote the region lying in the first quadrant, enclosed by the parabola $y^2=x$, the curve $S$, and the lines $x=1$ and $x=4$.
Then which of the following statements is (are) TRUE?
Let $P\left(x_1, y_1\right)$ and $Q\left(x_2, y_2\right)$ be two distinct points on the ellipse
$$ \frac{x^2}{9}+\frac{y^2}{4}=1 $$
such that $y_1>0$, and $y_2>0$. Let $C$ denote the circle $x^2+y^2=9$, and $M$ be the point $(3,0)$.
Suppose the line $x=x_1$ intersects $C$ at $R$, and the line $x=x_2$ intersects C at $S$, such that the $y$-coordinates of $R$ and $S$ are positive. Let $\angle R O M=\frac{\pi}{6}$ and $\angle S O M=\frac{\pi}{3}$, where $O$ denotes the origin $(0,0)$. Let $|X Y|$ denote the length of the line segment $X Y$.
Then which of the following statements is (are) TRUE?
Let ℝ denote the set of all real numbers. Let f: ℝ → ℝ be defined by
$f(x) = \begin{cases} \dfrac{6x + \sin x}{2x + \sin x}, & \text{if } x \neq 0, \\ \dfrac{7}{3}, & \text{if } x = 0. \end{cases}$
Then which of the following statements is (are) TRUE?
Let $y(x)$ be the solution of the differential equation
$$ x^2 \frac{d y}{d x}+x y=x^2+y^2, \quad x>\frac{1}{e} $$
satisfying $y(1)=0$. Then the value of $2 \frac{(y(e))^2}{y\left(e^2\right)}$ is ____________.
Let $a_0, a_1, \ldots, a_{23}$ be real numbers such that
$$ \left(1+\frac{2}{5} x\right)^{23}=\sum\limits_{i=0}^{23} a_i x^i $$
for every real number $x$. Let $a_r$ be the largest among the numbers $a_j$ for $0 \leq j \leq 23$. Then the value of $r$ is ____________.
A factory has a total of three manufacturing units, $M_1, M_2$, and $M_3$, which produce bulbs independent of each other. The units $M_1, M_2$, and $M_3$ produce bulbs in the proportions of $2: 2: 1$, respectively. It is known that $20 \%$ of the bulbs produced in the factory are defective. It is also known that, of all the bulbs produced by $M_1, 15 \%$ are defective. Suppose that, if a randomly chosen bulb produced in the factory is found to be defective, the probability that it was produced by $M_2$ is $\frac{2}{5}$.
If a bulb is chosen randomly from the bulbs produced by $M_3$, then the probability that it is defective is __________.
Consider the vectors
$$ \vec{x}=\hat{\imath}+2 \hat{\jmath}+3 \hat{k}, \quad \vec{y}=2 \hat{\imath}+3 \hat{\jmath}+\hat{k}, \quad \text { and } \quad \vec{z}=3 \hat{\imath}+\hat{\jmath}+2 \hat{k} $$
For two distinct positive real numbers $\alpha$ and $\beta$, define
$$ \vec{X}=\alpha \vec{x}+\beta \vec{y}-\vec{z}, \quad \vec{Y}=\alpha \vec{y}+\beta \vec{z}-\vec{x}, \quad \text { and } \quad \vec{Z}=\alpha \vec{z}+\beta \vec{x}-\vec{y} . $$
If the vectors $\vec{X}, \vec{Y}$, and $\vec{Z}$ lie in a plane, then the value of $\alpha+\beta-3$ is ____________.
For a non-zero complex number $z$, let $\arg (z)$ denote the principal argument of $z$, with $-\pi<\arg (z) \leq \pi$. Let $\omega$ be the cube root of unity for which $0<\arg (\omega)<\pi$. Let
$$ \alpha=\arg \left(\sum\limits_{n=1}^{2025}(-\omega)^n\right) $$
Then the value of $\frac{3 \alpha}{\pi}$ is ________________.
Let $\mathbb{R}$ denote the set of all real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow(0,4)$ be functions defined by
$$ f(x)=\log _e\left(x^2+2 x+4\right), \text { and } g(x)=\frac{4}{1+e^{-2 x}} $$
Define the composite function $f \circ g^{-1}$ by $\left(f \circ g^{-1}\right)(x)=f\left(g^{-1}(x)\right)$, where $g^{-1}$ is the inverse of the function $g$.
Then the value of the derivative of the composite function $f \circ g^{-1}$ at $x=2$ is ________________.
Let
$$ \alpha=\frac{1}{\sin 60^{\circ} \sin 61^{\circ}}+\frac{1}{\sin 62^{\circ} \sin 63^{\circ}}+\cdots+\frac{1}{\sin 118^{\circ} \sin 119^{\circ}} $$
Then the value of
$$ \left(\frac{\operatorname{cosec} 1^{\circ}}{\alpha}\right)^2 $$
is _____________.
If
$$ \alpha=\int\limits_{\frac{1}{2}}^2 \frac{\tan ^{-1} x}{2 x^2-3 x+2} d x $$
then the value of $\sqrt{7} \tan \left(\frac{2 \alpha \sqrt{7}}{\pi}\right)$ is _________.
(Here, the inverse trigonometric function $\tan ^{-1} x$ assumes values in $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.)
Physics
A temperature difference can generate e.m.f. in some materials. Let S be the e.m.f. produced per unit temperature difference between the ends of a wire, σ the electrical conductivity and κ the thermal conductivity of the material of the wire. Taking M, L, T, I and K as dimensions of mass, length, time, current and temperature, respectively, the dimensional formula of the quantity $Z = \frac{S^2 \sigma}{\kappa}$ is :
Two co-axial conducting cylinders of same length $\ell$ with radii $\sqrt{2}R$ and $2R$ are kept, as shown in Fig. 1. The charge on the inner cylinder is $Q$ and the outer cylinder is grounded. The annular region between the cylinders is filled with a material of dielectric constant $\kappa=5$. Consider an imaginary plane of the same length $\ell$ at a distance $R$ from the common axis of the cylinders. This plane is parallel to the axis of the cylinders. The cross-sectional view of this arrangement is shown in Fig. 2. Ignoring edge effects, the flux of the electric field through the plane is ($\epsilon_0$ is the permittivity of free space):

As shown in the figures, a uniform rod OO' of length l is hinged at the point O and held in place vertically between two walls using two massless springs of same spring constant. The springs are connected at the midpoint and at the top-end (O') of the rod, as shown in Fig. 1 and the rod is made to oscillate by a small angular displacement. The frequency of oscillation of the rod is f₁. On the other hand, if both the springs are connected at the midpoint of the rod, as shown in Fig. 2 and the rod is made to oscillate by a small angular displacement, then the frequency of oscillation is f₂. Ignoring gravity and assuming motion only in the plane of the diagram, the value of $ \frac{f_1}{f_2} $ is:

Consider a star of mass m2 kg revolving in a circular orbit around another star of mass m1 kg with m1 \gg m2. The heavier star slowly acquires mass from the lighter star at a constant rate of $\gamma$ kg/s. In this transfer process, there is no other loss of mass. If the separation between the centers of the stars is r, then its relative rate of change $\frac{1}{r}\frac{dr}{dt}$ (in s−1) is given by:
A positive point charge of $10^{-8}$ C is kept at a distance of 20 cm from the center of a neutral conducting sphere of radius 10 cm. The sphere is then grounded and the charge on the sphere is measured. The grounding is then removed and subsequently the point charge is moved by a distance of 10 cm further away from the center of the sphere along the radial direction. Taking $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9$ Nm$^2$/C$^2$ (where $\epsilon_0$ is the permittivity of free space), which of the following statements is/are correct:
Two identical concave mirrors each of focal length f are facing each other as shown in the schematic diagram. The focal length f is much larger than the size of the mirrors. A glass slab of thickness t and refractive index n_0 is kept equidistant from the mirrors and perpendicular to their common principal axis. A monochromatic point light source S is embedded at the center of the slab on the principal axis, as shown in the schematic diagram. For the image to be formed on S itself, which of the following distances between the two mirrors is/are correct:
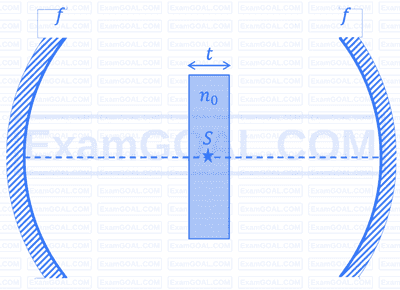
Six infinitely large and thin non-conducting sheets are fixed in configurations I and II. As shown in the figure, the sheets carry uniform surface charge densities which are indicated in terms of $\sigma_0$. The separation between any two consecutive sheets is $1~\mu \text{m}$. The various regions between the sheets are denoted as 1, 2, 3, 4 and 5. If $\sigma_0 = 9~\mu\text{C/m}^2$, then which of the following statements is/are correct:
(Take permittivity of free space $\epsilon_0 = 9 \times 10^{-12}$ F/m)

The efficiency of a Carnot engine operating with a hot reservoir kept at a temperature of 1000 K is 0.4 . It extracts 150 J of heat per cycle from the hot reservoir. The work extracted from this engine is being fully used to run a heat pump which has a coefficient of performance 10 . The hot reservoir of the heat pump is at a temperature of 300 K . Which of the following statements is/are correct :