Chemistry
Pt(s) | H2 (g, 1 bar) | H+ (aq, 1 M) || M4+ (aq), M2+ (aq) | Pt (s)
Ecell = 0.092 V when $${{\left[ {{M^{2 + }}(aq)} \right]} \over {\left[ {{M^{4 + }}(aq)} \right]}}$$ = 10x
Give, $$E_{{M^{4+}}/{M^{2 + }}}^o$$ = 0.151 V; 2.303 RT/F = 0.059 V
The value of x is
Thermal decomposition of gaseous X2 to gaseous X at 298 K takes place according to the following equations:
X2 (g) $$\leftrightharpoons$$ 2X (g)
The standard reaction Gibbs energy, $$\Delta _rG^o$$, of this reaction is positive. At the start of the reaction, there is one mole of X2 and no X. As the reaction proceeds, the number of moles of X formed is given by $$\beta$$. Thus, $$\beta _{equilibrium}$$ is the number of moles of X formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally. (Given R = 0.083 L bar K-1 mol-1)
Question
The INCORRECT statement among the following for this reaction, is
Thermal decomposition of gaseous X2 to gaseous X at 298 K takes place according to the following equations:
X2 (g) $$\leftrightharpoons$$ 2X (g)
The standard reaction Gibbs energy, $$\Delta _rG^o$$, of this reaction is positive. At the start of the reaction, there is one mole of X2 and no X. As the reaction proceeds, the number of moles of X formed is given by $$\beta$$. Thus, $$\beta _{equilibrium}$$ is the number of moles of X formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally. (Given R = 0.083 L bar K-1 mol-1)
Question
The equilibrium constant Kp for this reaction at 298 K, in terms of $$\beta _{equilibrium}$$, is
The correct order of acidity for the following compounds is

The major product of the following reaction sequence is:

In the following reaction, sequence in aqueous solution, the species X, Y and Z, respectively, are
$${S_2}O_3^{2 - }\buildrel {A{g^ + }} \over \longrightarrow \mathop X\limits_{Clear\,solution} \buildrel {A{g^ + }} \over \longrightarrow \mathop Y\limits_{White\,precipitate} \buildrel {With\,time} \over \longrightarrow \mathop Z\limits_{Black\,precipitate} $$
The qualitative sketches I, II and III given below show the variation of surface tension with molar concentration of three different aqueous solutions of KCl, CH3OH and CH3(CH2)11 OSO$$_3^ - $$ Na+ at room temperature. The correct assignment of the sketches is

For "invert sugar", the correct statement(s) is(are)
(Given : specific rotations of (+)-sucrose, (+)-maltose, L-($$-$$)-glucose and L-(+)-fructose in aqueous solution are +66$$^\circ$$, +140$$^\circ$$, $$-$$52$$^\circ$$ and +92$$^\circ$$, respectively.)
Among the following reaction(s), which gives(give) tert-butyl benzene as the major product is(are)
Reagent(s) which can be used to bring about the following transformation is(are)

The nitrogen containing compound produced in the reaction of HNO3 with P4O10
The compound R is
The compound T is
Mathematics
$$S = \left\{ {Z \in C:Z = {1 \over {a + ibt}}, + \in R,t \ne 0} \right\}$$, where $$i = \sqrt { - 1} $$. Ifz = x + iy and z $$ \in $$ S, then (x, y) lies on
$$\sum\limits_{k = 1}^{13} {{1 \over {\sin \left( {{\pi \over 4} + {{\left( {k - 1} \right)\pi } \over 6}} \right)\sin \left( {{\pi \over 4} + {{k\pi } \over 6}} \right)}}} $$ is equal to
$$\widehat w = {1 \over {\sqrt 6 }}\left( {\widehat i + \widehat j + 2\widehat k} \right).$$ Given that there exists a vector $${\overrightarrow v }$$ in $${{R^3}}$$ such that $$\left| {\widehat u \times \overrightarrow v } \right| = 1$$ and $$\widehat w.\left( {\widehat u \times \overrightarrow v } \right) = 1.$$ Which of the following statement(s) is (are) correct?
$$P\,\left( {X = Y} \right)$$ is
$$\,\,\,\,P\,\left( {X > Y} \right)$$ is
$$f\left( x \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {{{{n^n}\left( {x + n} \right)\left( {x + {n \over 2}} \right)...\left( {x + {n \over n}} \right)} \over {n!\left( {{x^2} + {n^2}} \right)\left( {{x^2} + {{{n^2}} \over 4}} \right)....\left( {{x^2} + {{{n^2}} \over {{n^2}}}} \right)}}} \right)^{{x \over n}}},$$ for
all $$x>0.$$ Then
$$\left\{ {\left( {x,y} \right) \in {R^2}:y \ge \sqrt {\left| {x + 3} \right|} ,5y \le x + 9 \le 15} \right\}$$
is equal to
$$\mathop {\lim }\limits_{x \to 2} {{f\left( x \right)g\left( x \right)} \over {f'\left( x \right)g'\left( x \right)}} = 1,$$ then
The orthocentre of the triangle $${F_1}MN$$ is
If the tangents to the ellipse at $$M$$ and $$N$$ meet at $$R$$ and the normal to the parabola at $$M$$ meets the $$x$$-axis at $$Q$$, then the ratio of area of the triangle $$MQR$$ to area of the quadrilateral $$M{F_1}N{F_2}$$is
Let $$P = \left[ {\matrix{ 1 & 0 & 0 \cr 4 & 1 & 0 \cr {16} & 4 & 1 \cr } } \right]$$ and I be the identity matrix of order 3. If $$Q = [{q_{ij}}]$$ is a matrix such that $${P^{50}} - Q = I$$ and $${{{q_{31}} + {q_{32}}} \over {{q_{21}}}}$$ equals
Let bi > 1 for I = 1, 2, ......, 101. Suppose logeb1, logeb2, ......., logeb101 are in Arithmetic Progression (A.P.) with the common difference loge2. Suppose a1, a2, ......, a101 are in A.P. such that a1 = b1 and a51 = b51. If t = b1 + b2 + .... + b51 and s = a1 + a2 + ..... + a51, then
Let a, b $$\in$$ R and f : R $$\to$$ R be defined by $$f(x) = a\cos (|{x^3} - x|) + b|x|\sin (|{x^3} + x|)$$. Then f is
Let a, $$\lambda$$, m $$\in$$ R. Consider the system of linear equations
ax + 2y = $$\lambda$$
3x $$-$$ 2y = $$\mu$$
Which of the following statements is(are) correct?
Let $$f:\left[ { - {1 \over 2},2} \right] \to R$$ and $$g:\left[ { - {1 \over 2},2} \right] \to R$$ be function defined by $$f(x) = [{x^2} - 3]$$ and $$g(x) = |x|f(x) + |4x - 7|f(x)$$, where [y] denotes the greatest integer less than or equal to y for $$y \in R$$. Then
Physics
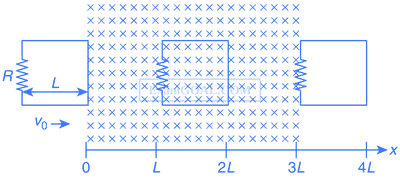
(i) when the block is at x0; and
(ii) when the block is at x = x0 + A.
In both cases, a particle with mass m( < M) is softly placed on the block after which they stick on each other. Which of the following statement(s) is(are) true about the motion after the mass m is placed on the mass M?


The measured masses of the neutron, $$_1^1H$$, $$_7^{15}N$$ and $$_8^{15}O$$ are 1.008665u, 1.007825u, 15.000109u and 15.003065u, respectively. Given that the radii of both the $$_7^{15}N$$ and $$_8^{15}O$$ nuclei are same, 1 u = 931.5 MeV/c2 (c is the speed of light) and e2/(4$$\pi$$$${{\varepsilon _0}}$$) = 1.44 MeV fm. Assuming that the difference between the binding energies of $$_7^{15}N$$ and $$_8^{15}O$$ is purely due to the electrostatic energy, the radius of either of the nuclei is (1 fm = 10$$-$$15 m)
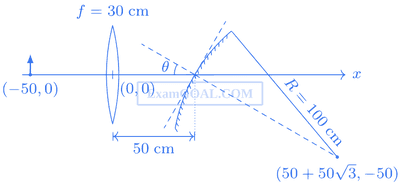
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x, y) at which the image is formed are
Which of the following schematic plot(s) is (are) correct? (Ignore gravity)

Which of the following is(are) true of the intensity pattern on the screen?

$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The distance r of the block at time t is
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The net reaction of the disc on the block is

Which one of the following statement is correct?

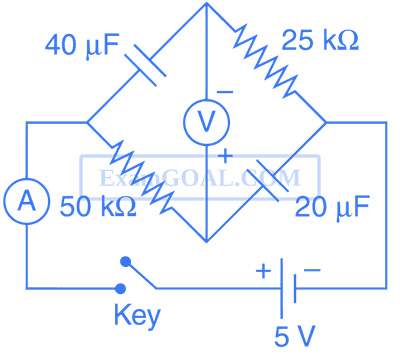
The average current in the steady state registered by the ammeter in the circuit will be