JEE Advanced 2021 Paper 2 Online
Paper was held on
Sun, Oct 3, 2021 2:30 AM
Chemistry
1
The reaction sequence(s) that would lead to o-xylene as the major product is(are)
2
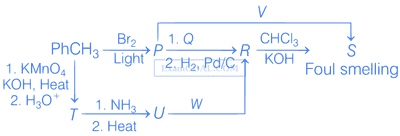
Correct option(s) for the following sequence of reactions is(are)

3
For the following reaction,
$$2X + Y\buildrel k \over \longrightarrow P$$ the rate of reaction is $${{d[P]} \over {dt}} = k[X]$$. Two moles of X are mixed with one mole of Y to make 1.0 L of solution. At 50 s, 0.5 mole of Y is left in the reaction mixture. The correct statement(s) about the reaction is(are)
(Use : ln 2 = 0.693)
$$2X + Y\buildrel k \over \longrightarrow P$$ the rate of reaction is $${{d[P]} \over {dt}} = k[X]$$. Two moles of X are mixed with one mole of Y to make 1.0 L of solution. At 50 s, 0.5 mole of Y is left in the reaction mixture. The correct statement(s) about the reaction is(are)
(Use : ln 2 = 0.693)
4
Some standard electrode potentials at 298 K are given below :
Pb2+ /Pb = $$- $$0.13 V
Ni2+ /Ni = $$-$$ 0.24 V
Cd2+ /Cd = $$-$$ 0.40 V
Fe2+ /Fe = $$-$$ 0.44 V
To a solution containing 0.001 M of X2+ and 0.1 M of Y2+, the metal rods X and Y are inserted (at 298 K) and connected by a conducting wire. This resulted in dissolution of X. The correct combination(s) of X and Y, respectively, is(are)
(Given : Gas constant, R = 8.314 J K$$-$$ mol$$-$$1, Faraday constant, F = 96500 C mol$$-$$1)
Pb2+ /Pb = $$- $$0.13 V
Ni2+ /Ni = $$-$$ 0.24 V
Cd2+ /Cd = $$-$$ 0.40 V
Fe2+ /Fe = $$-$$ 0.44 V
To a solution containing 0.001 M of X2+ and 0.1 M of Y2+, the metal rods X and Y are inserted (at 298 K) and connected by a conducting wire. This resulted in dissolution of X. The correct combination(s) of X and Y, respectively, is(are)
(Given : Gas constant, R = 8.314 J K$$-$$ mol$$-$$1, Faraday constant, F = 96500 C mol$$-$$1)
5
The pair(s) of complexes wherein both exhibit tetrahedral geometry is(are)
(Note : py = pyridine)
Given : Atomic numbers of Fe, Co, Ni and Cu are 26, 27, 28 and 29, respectively)
(Note : py = pyridine)
Given : Atomic numbers of Fe, Co, Ni and Cu are 26, 27, 28 and 29, respectively)
6
The correct statement(s) related to oxoacids of phosphorous is(are)
7
At 298 K, the limiting molar conductivity of a weak monobasic acid is 4 $$\times$$ 102 S cm2 mol$$-$$1. At 298 K, for an aqueous solution of the acid the degree of dissociation is $$\alpha$$ and the molar conductivity is y $$\times$$ 102 S cm2 mol$$-$$1. At 298 K, upon 20 times dilution with water, the molar conductivity of the solution becomes 3y $$\times$$ 102 S cm2 mol$$-$$1.
The value of $$\alpha$$ is __________.
The value of $$\alpha$$ is __________.
8
At 298 K, the limiting molar conductivity of a weak monobasic acid is 4 $$\times$$ 102 S cm2 mol$$-$$1. At 298 K, for an aqueous solution of the acid the degree of dissociation is $$\alpha$$ and the molar conductivity is y $$\times$$ 102 S cm2 mol$$-$$1. At 298 K, upon 20 times dilution with water, the molar conductivity of the solution becomes 3y $$\times$$ 102 S cm2 mol$$-$$1.
The value of y is __________.
The value of y is __________.
9
Reaction of x g of Sn with HCl quantitatively produced a salt. Entire amount of the salt reacted with y g of nitrobenzene in the presence of required amount of HCl to produce 1.29 g of an organic salt (quantitatively).
(Use Molar masses (in g mol$$-$$1) of H, C, N, O, Cl and Sn as 1, 12, 14, 16, 35 and 119, respectively).
The value of x is _________.
(Use Molar masses (in g mol$$-$$1) of H, C, N, O, Cl and Sn as 1, 12, 14, 16, 35 and 119, respectively).
The value of x is _________.
10
Reaction of x g of Sn with HCl quantitatively produced a salt. Entire amount of the salt reacted with y g of nitrobenzene in the presence of required amount of HCl to produce 1.29 g of an organic salt (quantitatively).
(Use Molar masses (in g mol$$-$$1) of H, C, N, O, Cl and Sn as 1, 12, 14, 16, 35 and 119, respectively).
The value of y is _________.
(Use Molar masses (in g mol$$-$$1) of H, C, N, O, Cl and Sn as 1, 12, 14, 16, 35 and 119, respectively).
The value of y is _________.
11
A sample (5.6 g) containing iron is completely dissolved in cold dilute HCl to prepare a 250 mL of solution. Titration of 25.0 mL of this solution requires 12.5 mL of 0.03 M KMnO4 solution to reach the end point. Number of moles of Fe2+ present in 250 mL solution is x $$\times$$ 10$$-$$2 (consider complete dissolution of FeCl2). The amount of iron present in the sample is y% by weight.
(Assume : KMnO4 reacts only with Fe2+ in the solution
Use : Molar mass of iron as 56 g mol$$-$$1)
The value of x is ______.
(Assume : KMnO4 reacts only with Fe2+ in the solution
Use : Molar mass of iron as 56 g mol$$-$$1)
The value of x is ______.
12
A sample (5.6 g) containing iron is completely dissolved in cold dilute HCl to prepare a 250 mL of solution. Titration of 25.0 mL of this solution requires 12.5 mL of 0.03 M KMnO4 solution to reach the end point. Number of moles of Fe2+ present in 250 mL solution is x $$\times$$ 10$$-$$2 (consider complete dissolution of FeCl2). The amount of iron present in the sample is y% by weight.
(Assume : KMnO4 reacts only with Fe2+ in the solution
Use : Molar mass of iron as 56 g mol$$-$$1)
The value of y is ______.
(Assume : KMnO4 reacts only with Fe2+ in the solution
Use : Molar mass of iron as 56 g mol$$-$$1)
The value of y is ______.
13
Correct match of the C-H bonds (shown in bold) in Column J with their BDE in Column K is
| Column J Molecule |
Column K BDE (kcal $$mo{l^{ - 1}}$$) |
|---|---|
| (P) H-CH($$C{H_3}$$)$$_2$$ | (i) 132 |
| (Q) H-CH$$_2$$Ph | (ii) 110 |
| (R) H-CH=CH$$_2$$ | (iii) 95 |
| (S) H-C $$ \equiv $$ CH | (iv) 88 |
14
For the following reaction
CH4(g) + Cl2(g) $$\buildrel {light} \over \longrightarrow $$ CH3Cl(g) + HCl (g)
the correct statement is
CH4(g) + Cl2(g) $$\buildrel {light} \over \longrightarrow $$ CH3Cl(g) + HCl (g)
the correct statement is
15
Precipitate X is
16
Among the following, the brown ring is due to the formation of
17
One mole of an ideal gas at 900 K, undergoes two reversible processes, I followed by II, as shown below. If the work done by the gas in the two processes are same, the value of $$\ln {{{V_3}} \over {{V_2}}}$$ is _________.
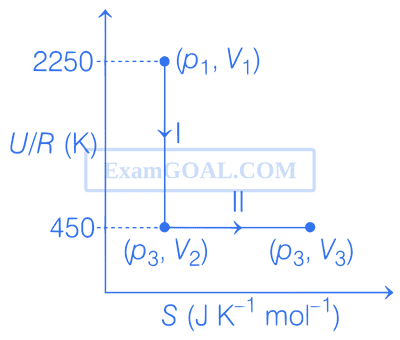
(U : internal energy, S : entropy, p : pressure, V : volume, R : gas constant)
(Given : molar heat capacity at constant volume, CV,m of the gas is $${5 \over 2}$$R)

(U : internal energy, S : entropy, p : pressure, V : volume, R : gas constant)
(Given : molar heat capacity at constant volume, CV,m of the gas is $${5 \over 2}$$R)
18
Consider a helium (He) atom that absorbs a photon of wavelength 330 nm. The change in the velocity (in cm s$$-$$1) of He atom after the photon absorption is __________.
(Assume : Momentum is conserved when photon is absorbed.
Use : Planck constant = 6.6 $$\times$$ 10$$-$$34 J s, Avogadro number = 6 $$\times$$ 1023 mol$$-$$1, Molar mass of He = 4 g mol$$-$$1)
(Assume : Momentum is conserved when photon is absorbed.
Use : Planck constant = 6.6 $$\times$$ 10$$-$$34 J s, Avogadro number = 6 $$\times$$ 1023 mol$$-$$1, Molar mass of He = 4 g mol$$-$$1)
19
Ozonolysis of ClO2 produces an oxide of chlorine. The average oxidation state of chlorine in this oxide is __________.
Mathematics
1
Let
$${S_1} = \left\{ {(i,j,k):i,j,k \in \{ 1,2,....,10\} } \right\}$$,
$${S_2} = \left\{ {(i,j):1 \le i < j + 2 \le 10,i,j \in \{ 1,2,...,10\} } \right\}$$,
$${S_3} = \left\{ {(i,j,k,l):1 \le i < j < k < l,i,j,k,l \in \{ 1,2,...,10\} } \right\}$$ and
$${S_4} = \{ (i,j,k,l):i,j,k$$ and $$l$$ are distinct elements in {1, 2, ...., 10}.
If the total number of elements in the set Sr is nr, r = 1, 2, 3, 4, then which of the following statements is(are) TRUE?
$${S_1} = \left\{ {(i,j,k):i,j,k \in \{ 1,2,....,10\} } \right\}$$,
$${S_2} = \left\{ {(i,j):1 \le i < j + 2 \le 10,i,j \in \{ 1,2,...,10\} } \right\}$$,
$${S_3} = \left\{ {(i,j,k,l):1 \le i < j < k < l,i,j,k,l \in \{ 1,2,...,10\} } \right\}$$ and
$${S_4} = \{ (i,j,k,l):i,j,k$$ and $$l$$ are distinct elements in {1, 2, ...., 10}.
If the total number of elements in the set Sr is nr, r = 1, 2, 3, 4, then which of the following statements is(are) TRUE?
2
Consider a triangle PQR having sides of lengths p, q and r opposite to the angles P, Q and R, respectively. Then which of the following statements is (are) TRUE?
3
Let $$f:\left[ { - {\pi \over 2},{\pi \over 2}} \right] \to R$$ be a continuous function such that $$f(0) = 1$$ and $$\int_0^{{\pi \over 3}} {f(t)dt = 0} $$. Then which of the following statements is(are) TRUE?
4
For any real numbers $$\alpha$$ and $$\beta$$, let $${y_{\alpha ,\beta }}(x)$$, x$$\in$$R, be the solution of the differential equation $${{dy} \over {dx}} + \alpha y = x{e^{\beta x}},y(1) = 1$$. Let $$S = \{ {y_{\alpha ,\beta }}(x):\alpha ,\beta \in R\} $$. Then which of the following functions belong(s) to the set S?
5
Let O be the origin and $$\overrightarrow {OA} = 2\widehat i + 2\widehat j + \widehat k$$ and $$\overrightarrow {OB} = \widehat i - 2\widehat j + 2\widehat k$$ and $$\overrightarrow {OC} = {1 \over 2}\left( {\overrightarrow {OB} - \lambda \overrightarrow {OA} } \right)$$ for some $$\lambda$$ > 0. If $$\left| {\overrightarrow {OB} \times \overrightarrow {OC} } \right| = {9 \over 2}$$, then which of the following statements is (are) TRUE?
6
Let E denote the parabola y2 = 8x. Let P = ($$-$$2, 4), and let Q and Q' be two distinct points on E such that the lines PQ and PQ' are tangents to E. Let F be the focus of E. Then which of the following statements is(are) TRUE?
7
Consider the region R = {(x, y) $$\in$$ R $$\times$$ R : x $$\ge$$ 0 and y2 $$\le$$ 4 $$-$$ x}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F. Let ($$\alpha$$, $$\beta$$) be a point where the circle C meets the curve y2 = 4 $$-$$ x.
The radius of the circle C is ___________.
The radius of the circle C is ___________.
8
Consider the region R = {(x, y) $$\in$$ R $$\times$$ R : x $$\ge$$ 0 and y2 $$\le$$ 4 $$-$$ x}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F. Let ($$\alpha$$, $$\beta$$) be a point where the circle C meets the curve y2 = 4 $$-$$ x.
The value of $$\alpha$$ is ___________.
The value of $$\alpha$$ is ___________.
9
Let f1 : (0, $$\infty$$) $$\to$$ R and f2 : (0, $$\infty$$) $$\to$$ R be defined by $${f_1}(x) = \int\limits_0^x {\prod\limits_{j = 1}^{21} {{{(t - j)}^j}dt} } $$, x > 0 and $${f_2}(x) = 98{(x - 1)^{50}} - 600{(x - 1)^{49}} + 2450,x > 0$$, where, for any positive integer n and real numbers a1, a2, ....., an, $$\prod\nolimits_{i = 1}^n {{a_i}} $$ denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, $$\infty$$).
The value of $$2{m_1} + 3{n_1} + {m_1}{n_1}$$ is ___________.
The value of $$2{m_1} + 3{n_1} + {m_1}{n_1}$$ is ___________.
10
Let f1 : (0, $$\infty$$) $$\to$$ R and f2 : (0, $$\infty$$) $$\to$$ R be defined by $${f_1}(x) = \int\limits_0^x {\prod\limits_{j = 1}^{21} {{{(t - j)}^j}dt} } $$, x > 0 and $${f_2}(x) = 98{(x - 1)^{50}} - 600{(x - 1)^{49}} + 2450,x > 0$$, where, for any positive integer n and real numbers a1, a2, ....., an, $$\prod\nolimits_{i = 1}^n {{a_i}} $$ denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, $$\infty$$).
The value of $$6{m_2} + 4{n_2} + 8{m_2}{n_2}$$ is ___________.
The value of $$6{m_2} + 4{n_2} + 8{m_2}{n_2}$$ is ___________.
11
Let $${g_i}:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R,i = 1,2$$, and $$f:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R$$ be functions such that $${g_1}(x) = 1,{g_2}(x) = |4x - \pi |$$ and $$f(x) = {\sin ^2}x$$, for all $$x \in \left[ {{\pi \over 8},{{3\pi } \over 8}} \right]$$. Define $${S_i} = \int\limits_{{\pi \over 8}}^{{{3\pi } \over 8}} {f(x).{g_i}(x)dx} $$, i = 1, 2
The value of $${{16{S_1}} \over \pi }$$ is _____________.
The value of $${{16{S_1}} \over \pi }$$ is _____________.
12
Let $${g_i}:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R,i = 1,2$$, and $$f:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R$$ be functions such that $${g_1}(x) = 1,{g_2}(x) = |4x - \pi |$$ and $$f(x) = {\sin ^2}x$$, for all $$x \in \left[ {{\pi \over 8},{{3\pi } \over 8}} \right]$$. Define $${S_i} = \int\limits_{{\pi \over 8}}^{{{3\pi } \over 8}} {f(x).{g_i}(x)dx} $$, i = 1, 2
The value of $${{48{S_2}} \over {{\pi ^2}}}$$ is ___________.
The value of $${{48{S_2}} \over {{\pi ^2}}}$$ is ___________.
13
Consider M with $$r = {{1025} \over {513}}$$. Let k be the number of all those circles Cn that are inside M. Let l be the maximum possible number of circles among these k circles such that no two circles intersect. Then
14
Consider M with $$r = {{({2^{199}} - 1)\sqrt 2 } \over {{2^{198}}}}$$. The number of all those circles Dn that are inside M is
15
Which of the following statements is TRUE?
16
Which of the following statements is TRUE?
17
A number of chosen at random from the set {1, 2, 3, ....., 2000}. Let p be the probability that the chosen number is a multiple of 3 or a multiple of 7. Then the value of 500p is __________.
18
Let E be the ellipse $${{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1$$. For any three distinct points P, Q and Q' on E, let M(P, Q) be the mid-point of the line segment joining P and Q, and M(P, Q') be the mid-point of the line segment joining P and Q'. Then the maximum possible value of the distance between M(P, Q) and M(P, Q'), as P, Q and Q' vary on E, is _______.
19
For any real number x, let [ x ] denote the largest integer less than or equal to x. If $$I = \int\limits_0^{10} {\left[ {\sqrt {{{10x} \over {x + 1}}} } \right]dx} $$, then the value of 9I is __________.
Physics
1
One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q, at a height L above the hinge at point O. A block of weight $$\alpha$$W is attached at the point P of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of (2$$\sqrt 2 $$)W. Which of the following statement(s) is(are) correct?


2
A source, approaching with speed u towards the open end of a stationary pipe of length L, is emitting a sound of frequency fs. The farther end of the pipe is closed. The speed of sound in air is v and f0 is the fundamental frequency of the pipe. For which of the following combination(s) of u and fs, will the sound reaching the pipe lead to a resonance?
3
For a prism of prism angle $$\theta$$ = 60$$^\circ$$, the refractive indices of the left half and the right half are, respectively, n1 and n2 (n2 $$\ge$$ n1) as shown in the figure. The angle of incidence i is chosen such that the incident light rays will have minimum deviation if n1 = n2 = n = 1.5. For the case of unequal refractive indices, n1 = n and n2 = n + $$\Delta$$n (where $$\Delta$$n << n), the angle of emergence e = i + $$\Delta$$e. Which of the following statement(s) is(are) correct?
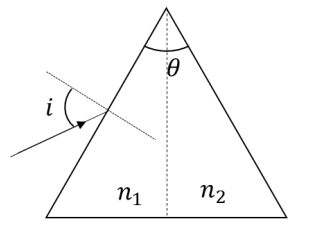

4
A physical quantity $$\overrightarrow S $$ is defined as $$\overrightarrow S = (\overrightarrow E \times \overrightarrow B )/{\mu _0}$$, where $$\overrightarrow E $$ is electric field, $$\overrightarrow B $$ is magnetic field and $$\mu$$0 is the permeability of free space. The dimensions of $$\overrightarrow S $$ are the same as the dimensions of which of the following quantity(ies)?
5
A heavy nucleus N, at rest, undergoes fission N $$\to$$ P + Q, where P and Q are two lighter nuclei. Let $$\delta$$ = MN $$-$$ MP $$-$$ MQ, where MP, MQ and MN are the masses of P, Q and N, respectively. EP and EQ are the kinetic energies of P and Q, respectively. The speeds of P and Q are vP and vQ, respectively. If c is the speed of light, which of the following statement(s) is(are) correct?
6
Two concentric circular loops, one of radius R and the other of radius 2R, lie in the xy-plane with the origin as their common center, as shown in the figure. The smaller loop carries current I1 in the anti-clockwise direction and the larger loop carries current I2 in the clockwise direction, with I2 > 2I1. $$\overrightarrow B $$(x, y) denotes the magnetic field at a point (x, y) in the xy-plane. Which of the following statement(s) is(are) correct?
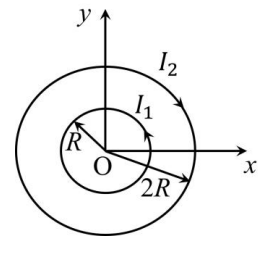

7
A soft plastic bottle, filled with water of density 1 gm/cc, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of 5 gm, and it is made of a thick glass of density 2.5 gm/cc. Initially the bottle is sealed at atmosphere pressure p0 = 105 Pa so that the volume of the trapped air is v0 = 3.3 cc. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure p0 + $$\Delta$$p without changing its orientation. At this pressure, the volume of the trapped air is v0 $$-$$ $$\Delta$$v. Let $$\Delta$$v = X cc and $$\Delta$$p = Y $$\times$$ 103 Pa.
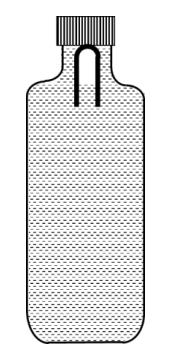
The value of X is _______________.

The value of X is _______________.
8
A soft plastic bottle, filled with water of density 1 gm/cc, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of 5 gm, and it is made of a thick glass of density 2.5 gm/cc. Initially the bottle is sealed at atmosphere pressure p0 = 105 Pa so that the volume of the trapped air is v0 = 3.3 cc. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure p0 + $$\Delta$$p without changing its orientation. At this pressure, the volume of the trapped air is v0 $$-$$ $$\Delta$$v. Let $$\Delta$$v = X cc and $$\Delta$$p = Y $$\times$$ 103 Pa.

The value of Y is _______________.

The value of Y is _______________.
9
A pendulum consists of a bob of mass m = 0.1 kg and a massless inextensible string of length L = 1.0 m. It is suspended from a fixed point at height H = 0.9 m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse P = 0.2 kg-m/s is imparted to the bob at some instant. After the bob slides for some distance, the string becomes taut and the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is J kg-m2/s. The kinetic energy of the pendulum just after the lift-off is K Joules.
The value of J is ___________.
The value of J is ___________.
10
A pendulum consists of a bob of mass m = 0.1 kg and a massless inextensible string of length L = 1.0 m. It is suspended from a fixed point at height H = 0.9 m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse P = 0.2 kg-m/s is imparted to the bob at some instant. After the bob slides for some distance, the string becomes taut and the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is J kg-m2/s. The kinetic energy of the pendulum just after the lift-off is K Joules.
The value of K is ___________.
The value of K is ___________.
11
In a circuit, a metal filament lamp is connected in series with a capacitor of capacitance C $$\mu$$F across a 200 V, 50 Hz supply. The power consumed by the lamp is 500 W while the voltage drop across it is 100 V. Assume that there is no inductive load in the circuit. Take rms values of the voltages. The magnitude of the phase-angle (in degrees) between the current and the supply voltage is $$\varphi $$. Assume, $$\pi$$$$\sqrt 3 $$ $$ \approx $$ 5.
The value of C is ____________.
The value of C is ____________.
12
In a circuit, a metal filament lamp is connected in series with a capacitor of capacitance C $$\mu$$F across a 200 V, 50 Hz supply. The power consumed by the lamp is 500 W while the voltage drop across it is 100 V. Assume that there is no inductive load in the circuit. Take rms values of the voltages. The magnitude of the phase-angle (in degrees) between the current and the supply voltage is $$\varphi $$. Assume, $$\pi$$$$\sqrt 3 $$ $$ \approx $$ 5.
The value of $$\varphi$$ is ____________.
The value of $$\varphi$$ is ____________.
13
When the dipole m is placed at a distance r from the center of the loop (as shown in the figure), the current induced in the loop will be proportional to
14
The work done in bringing the dipole from infinity to a distance r from the center of the loop by the given process is proportional to
15
The value of $${{{T_R}} \over {{T_0}}}$$ is
16
The value of $${Q \over {R{T_0}}}$$ is
17
In order to measure the internal resistance r1 of a cell of emf E, a meter bridge of wire resistance R0 = 50$$\Omega$$, a resistance R0/2, another cell of emf E/2 (internal resistance r) and a galvanometer G are used in a circuit, as shown in the figure. If the null point is found at l = 72 cm, then the value of r1 = __________ $$\Omega$$.
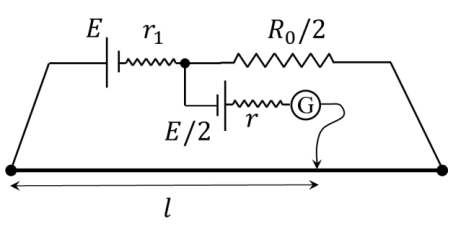

18
The distance between two stars of masses 3MS and 6MS is 9R. Here R is the mean distance between the centers of the Earth and the Sun, and MS is the mass of the Sun. The two stars orbit around their common center of mass in circular orbits with period nT, where T is the period of Earth's revolution around the Sun. The value of n is __________.
19
In a photoemission experiment, the maximum kinetic energies of photoelectrons from metals P, Q and R are EP, EQ and ER, respectively, and they are related by EP = 2EQ = 2ER. In this experiment, the same source of monochromatic light is used for metals P and Q while a different source of monochromatic light is used for the metal R. The work functions for metals P, Q and R are 4.0 eV, 4.5 eV and 5.5 eV, respectively. The energy of the incident photon used for metal R, in eV, is ___________.