IIT-JEE 2005 Screening
Paper was held on
Sun, May 22, 2005 9:00 AM
Chemistry
1
The elevation in boiling point of a solution of 13.44 g of CuCl2 in 1kg of water using the following information will be (Molecular weight of CuCl2 = 134.4 and Kb = 0.52 K molal-1)
2
Which species has the maximum number of lone pair of electrons on the central atom?
3
The number of radial nodes of 3s and 2p orbitals are respectively
Mathematics
1
$$\int\limits_{ - 2}^0 {\left\{ {{x^3} + 3{x^2} + 3x + 3 + \left( {x + 1} \right)\cos \left( {x + 1} \right)} \right\}\,\,dx} $$ is equal to
2
If $$\overrightarrow a \,,\,\overrightarrow b ,\overrightarrow c $$ are three non-zero, non-coplanar vectors and
$$\overrightarrow {{b_1}} = \overrightarrow b - {{\overrightarrow b .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a ,\overrightarrow {{b_2}} = \overrightarrow b + {{\overrightarrow b .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a ,$$
$$\overrightarrow {{c_1}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a + {{\overrightarrow b .\,\overrightarrow c } \over {{{\left| c \right|}^2}}}{\overrightarrow b _1},\,\,\overrightarrow {{c_2}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a - {{\overrightarrow b \,.\,\overrightarrow c } \over {{{\left| {{{\overrightarrow b }_1}} \right|}^2}}}{\overrightarrow b _1},$$
$$\overrightarrow {{c_3}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow c } \right|}^2}}}\overrightarrow a + {{\overrightarrow b .\,\overrightarrow c } \over {{{\left| c \right|}^2}}}{\overrightarrow b _1},\,\,\overrightarrow {{c_4}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow c } \right|}^2}}}\overrightarrow a - {{\overrightarrow b \,.\,\overrightarrow c } \over {{{\left| {{{\overrightarrow b }_1}} \right|}^2}}}{\overrightarrow b _1},$$
then the set of orthogonal vectors is
$$\overrightarrow {{b_1}} = \overrightarrow b - {{\overrightarrow b .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a ,\overrightarrow {{b_2}} = \overrightarrow b + {{\overrightarrow b .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a ,$$
$$\overrightarrow {{c_1}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a + {{\overrightarrow b .\,\overrightarrow c } \over {{{\left| c \right|}^2}}}{\overrightarrow b _1},\,\,\overrightarrow {{c_2}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow a } \right|}^2}}}\overrightarrow a - {{\overrightarrow b \,.\,\overrightarrow c } \over {{{\left| {{{\overrightarrow b }_1}} \right|}^2}}}{\overrightarrow b _1},$$
$$\overrightarrow {{c_3}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow c } \right|}^2}}}\overrightarrow a + {{\overrightarrow b .\,\overrightarrow c } \over {{{\left| c \right|}^2}}}{\overrightarrow b _1},\,\,\overrightarrow {{c_4}} = \overrightarrow c - {{\overrightarrow c .\,\overrightarrow a } \over {{{\left| {\overrightarrow c } \right|}^2}}}\overrightarrow a - {{\overrightarrow b \,.\,\overrightarrow c } \over {{{\left| {{{\overrightarrow b }_1}} \right|}^2}}}{\overrightarrow b _1},$$
then the set of orthogonal vectors is
3
A variable plane at a distance of the one unit from the origin cuts the coordinates axes at $$A,$$ $$B$$ and $$C.$$ If the centroid $$D$$ $$(x, y, z)$$ of triangle $$ABC$$ satisfies the relation $${1 \over {{x^2}}} + {1 \over {{y^2}}} + {1 \over {{z^2}}} = k,$$ then the value $$k$$ is
4
A six faced fair dice is thrown until $$1$$ comes, then the probability that $$1$$ comes in even no. of trials is
5
The differential equation $${{dy} \over {dx}} = {{\sqrt {1 - {y^2}} } \over y}$$ determines a family of circles with
6
The solution of primitive integral equation $$\left( {{x^2} + {y^2}} \right)dy = xy$$
$$dx$$ is $$y=y(x),$$ If $$y(1)=1$$ and $$\left( {{x_0}} \right) = e$$, then $${{x_0}}$$ is equal to
$$dx$$ is $$y=y(x),$$ If $$y(1)=1$$ and $$\left( {{x_0}} \right) = e$$, then $${{x_0}}$$ is equal to
7
For the primitive integral equation $$ydx + {y^2}dy = x\,dy;$$
$$x \in R,\,\,y > 0,y = y\left( x \right),\,y\left( 1 \right) = 1,$$ then $$y(-3)$$ is
$$x \in R,\,\,y > 0,y = y\left( x \right),\,y\left( 1 \right) = 1,$$ then $$y(-3)$$ is
8
If $$y=y(x)$$ and it follows the relation $$x\cos \,y + y\,cos\,x = \pi $$ then $$y''(0)=$$
9
The area bounded by the parabola $$y = {\left( {x + 1} \right)^2}$$ and
$$y = {\left( {x - 1} \right)^2}$$ and the line $$y=1/4$$ is
$$y = {\left( {x - 1} \right)^2}$$ and the line $$y=1/4$$ is
10
$$a,\,b,\,c$$ are integers, not all simultaneously equal and $$\omega $$ is cube root of unity $$\left( {\omega \ne 1} \right),$$ then minimum value of $$\left| {a + b\omega + c{\omega ^2}} \right|$$ is
11
If $$\int\limits_{\sin x}^1 {{t^2}f\left( t \right)dt = 1 - \sin x,} $$ then f$$\left( {{1 \over {\sqrt 3 }}} \right)$$ is
12
If $$P(x)$$ is a polynomial of degree less than or equal to $$2$$ and $$S$$ is the set of all such polynomials so that $$P(0)=0$$, $$P(1)=1$$ and $$P'\left( x \right) > 0\,\,\forall x \in \left[ {0,1} \right],$$ then
13
In a triangle $$ABC$$, $$a,b,c$$ are the lengths of its sides and $$A,B,C$$ are the angles of triangle $$ABC$$. The correct relation is given by
14
If $$f(x)$$ is a twice differentiable function and given that $$f\left( 1 \right) = 1;f\left( 2 \right) = 4,f\left( 3 \right) = 9$$, then
15
Tangent to the curve $$y = {x^2} + 6$$ at a point $$(1, 7)$$ touches the circle $${x^2} + {y^2} + 16x + 12y + c = 0$$ at a point $$Q$$. Then the coordinates of $$Q$$ are
16
The minimum area of triangle formed by the tangent to the $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ and coordinate axes is
17
A circle is given by $${x^2}\, + \,{(y\, - \,1\,)^2}\, = \,1$$, another circle C touches it externally and also the x-axis, then thelocus of its centre is
18
In the quadratic equation $$\,\,a{x^2} + bx + c = 0,$$ $$\Delta $$ $$ = {b^2} - 4ac$$ and $$\alpha + \beta ,\,{\alpha ^2} + {\beta ^2},\,{\alpha ^3} + {\beta ^3},$$ are in G.P. where $$\alpha ,\beta $$ are the root of $$\,\,a{x^2} + bx + c = 0,$$ then
19
If the LCM of p, q is $${r^2}\,{r^4}\,{s^2}$$, where r, s, t are prime numbers and p, q are the positive integers then number of ordered pair (p, q) is
20
A rectangle with sides of lenght (2m - 1) and (2n - 1) units is divided into squares of unit lenght by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is
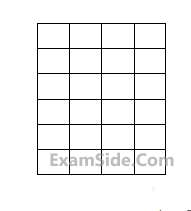

21
The value of $$$\left( {\matrix{
{30} \cr
0 \cr
} } \right)\left( {\matrix{
{30} \cr
{10} \cr
} } \right) - \left( {\matrix{
{30} \cr
1 \cr
} } \right)\left( {\matrix{
{30} \cr
{11} \cr
} } \right) + \left( {\matrix{
{30} \cr
2 \cr
} } \right)\left( {\matrix{
{30} \cr
{12} \cr
} } \right)....... + \left( {\matrix{
{30} \cr
{20} \cr
} } \right)\left( {\matrix{
{30} \cr
{30} \cr
} } \right)$$$
is where $$\left( {\matrix{ n \cr r \cr } } \right) = {}^n{C_r}$$
is where $$\left( {\matrix{ n \cr r \cr } } \right) = {}^n{C_r}$$
22
$$\cos \left( {\alpha - \beta } \right) = 1$$ and $$\,\cos \left( {\alpha + \beta } \right) = 1/e$$ where $$\alpha ,\,\beta \in \left[ { - \pi ,\pi } \right].$$
Paris of $$\alpha ,\,\beta $$ which satisfy both the equations is/are
Paris of $$\alpha ,\,\beta $$ which satisfy both the equations is/are
Physics
1
A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y = Kt2, (K = 1 m/s2) where y is the vertical displacement. The time period now become T2. The ratio of $${{T_1^2} \over {T_2^2}}$$ is (g = 10 m/s2)
2
Which of the following set have different dimensions?