By approximately matching the information given in the three columns of the following table.

Let f(x) = x + log_e x $$-$$ x log_e x, x$$ \in $$(0, $$\infty $$)

Column 1 contains information about zeroes of f(x), f'(x) and f"(x).

Column 2 contains information about the limiting behaviour of f(x), f'(x) and f"(x) at infinity.

Column 3 contains information about increasing/decreasing nature of f(x) and f'(x).

	Column - 1	Column - 2	Column - 3
(i)	f(x) = 0 for some $$x \in (1,{e^2})$$	(i) $$\mathop {\lim }\limits_{x \to \infty } \,f(x) = 0$$	f is increasing in (0, 1)
(ii)	f'(x) = 0 for some $$x \in (1,e)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f(x) = - \infty $$	f is decreasing in (e, $${e^2}$$)
(iii)	f'(x) = 0 for some $$x \in (0,1)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f'(x) = - \infty $$	f' is increasing in (0, 1)
(iv)	f'(x) = 0 for some $$x \in (1,e)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f'(x) = 0$$	f' is decreasing in (e, $${e^2}$$)

Which of the following options is the only CORRECT combination?

By approximately matching the information given in the three columns of the following table.

Let f(x) = x + log_e x $$-$$ x log_e x, x$$ \in $$(0, $$\infty $$)

Column 1 contains information about zeroes of f(x), f'(x) and f"(x).

Column 2 contains information about the limiting behaviour of f(x), f'(x) and f"(x) at infinity.

Column 3 contains information about increasing/decreasing nature of f(x) and f'(x).

	Column - 1	Column - 2	Column - 3
(i)	f(x) = 0 for some $$x \in (1,{e^2})$$	(i) $$\mathop {\lim }\limits_{x \to \infty } \,f(x) = 0$$	f is increasing in (0, 1)
(ii)	f'(x) = 0 for some $$x \in (1,e)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f(x) = - \infty $$	f is decreasing in (e, $${e^2}$$)
(iii)	f'(x) = 0 for some $$x \in (0,1)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f'(x) = - \infty $$	f' is increasing in (0, 1)
(iv)	f'(x) = 0 for some $$x \in (1,e)$$	$$\mathop {\lim }\limits_{x \to \infty } \,f'(x) = 0$$	f' is decreasing in (e, $${e^2}$$)

Which of the following options is the only CORRECT combination?

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case will the particle move in a straight line with constant velocity?

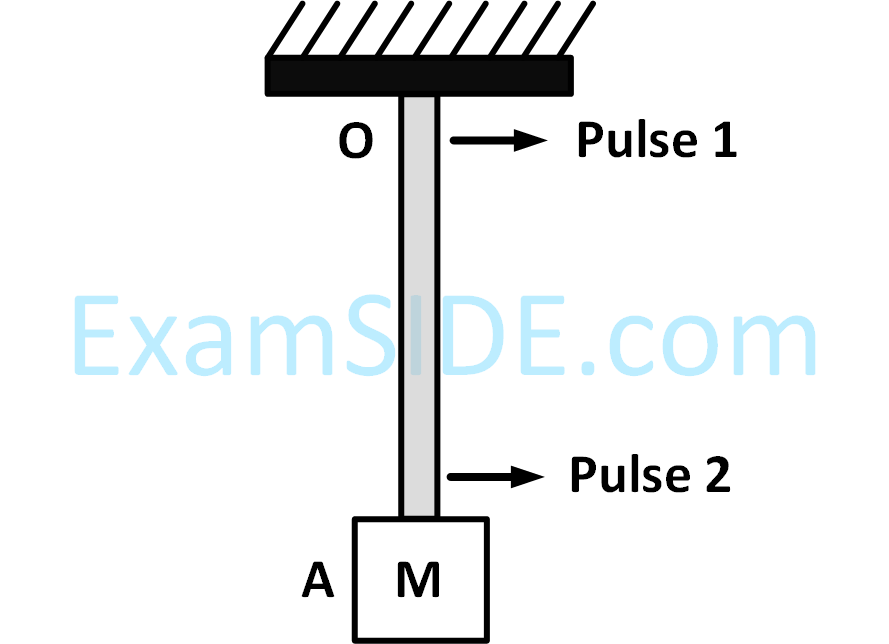
A block $$M$$ hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to fixed rigid support at $$O.$$ A transverse wave pulse (Pulse 1) of wavelength $${\lambda _0}$$ is produced at point $$O$$ on the rope. The pulse takes time $${T_{OA}}$$ to reach point $$A.$$ If the wave pulse of wavelength $${\lambda _0}$$ is produced at point $$A$$ (Pulse 2) without disturbing the position of $$M$$ it takes time $${T_{AO}}$$ to reach point $$O.$$ which of the following options is/are correct?