1
JEE Advanced 2017 Paper 1 Offline
MCQ (More than One Correct Answer)
+4
-1

A block of mass $$M$$ has a circular cut with a frictionless surface as shown. The block resets on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at $$x=0,$$ in a co-ordinate system fixed to the table. A point mass $$m$$ is released from rest at the topmost point of the path as shown and it slides down.
When the mass loses contact with the block, its position is $$x$$ and the velocity is $$v.$$ At that instant, which of the following options is/are correct?

When the mass loses contact with the block, its position is $$x$$ and the velocity is $$v.$$ At that instant, which of the following options is/are correct?

2
JEE Advanced 2017 Paper 1 Offline
MCQ (More than One Correct Answer)
+4
-2

A human body has a surface area of approximately $$1\,m{}^2.$$ The normal body temperature is $$10$$ $$K$$ above the surrounding room temperature $${T_0}.$$ Take the room temperature to be $${T_0} = 300K.$$ For $${T_0} = 300\,K,$$ the value of $$\sigma T_0^4 = 460\,W{m^{ - 2}}$$ (where $$\sigma $$ is the Stefan-Boltzmann constant).
Which of the following options is / are correct?
Which of the following options is / are correct?
3
JEE Advanced 2017 Paper 1 Offline
MCQ (More than One Correct Answer)
+4
-1

A circular insulated copper wire loop is twisted to form two loops of area $$A$$ and $$2A$$ as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field $$\overrightarrow B $$ points into the plane of the paper. At $$t=0,$$ the loop starts rotating about the common diameter as axis with a constant angular velocity $$\omega $$ in the magnetic field.
Which of the following options is/are correct?
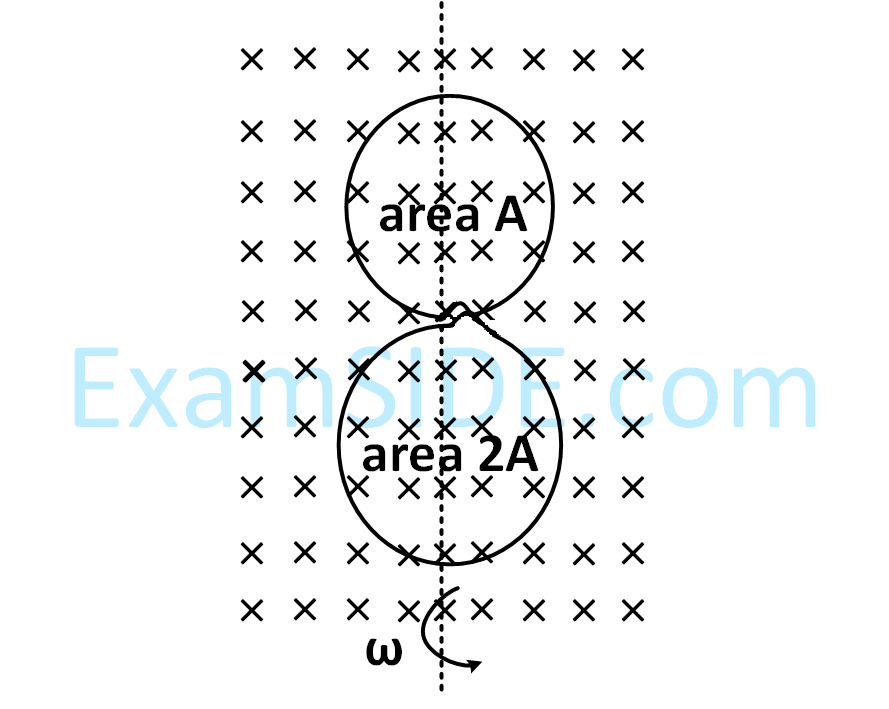
Which of the following options is/are correct?

4
JEE Advanced 2017 Paper 1 Offline
MCQ (More than One Correct Answer)
+4
-1

For an isosceles prism of angle $$A$$ and refractive index $$\mu $$, it is found that the angle of minimum deviation $${\delta _m} = A.$$
Which of the following options is/are correct?
Which of the following options is/are correct?
Paper analysis
Total Questions
Chemistry
18
Mathematics
18
Physics
18
More papers of JEE Advanced
JEE Advanced 2025 Paper 2 Online
JEE Advanced 2025 Paper 1 Online
JEE Advanced 2024 Paper 2 Online
JEE Advanced 2024 Paper 1 Online
JEE Advanced 2023 Paper 2 Online
JEE Advanced 2023 Paper 1 Online
JEE Advanced 2022 Paper 2 Online
JEE Advanced 2022 Paper 1 Online
JEE Advanced 2021 Paper 2 Online
JEE Advanced 2021 Paper 1 Online
JEE Advanced 2020 Paper 2 Offline
JEE Advanced 2020 Paper 1 Offline
JEE Advanced 2019 Paper 2 Offline
JEE Advanced 2019 Paper 1 Offline
JEE Advanced 2018 Paper 2 Offline
JEE Advanced 2018 Paper 1 Offline
JEE Advanced 2017 Paper 2 Offline
JEE Advanced 2017 Paper 1 Offline
JEE Advanced 2016 Paper 2 Offline
JEE Advanced 2016 Paper 1 Offline
JEE Advanced 2015 Paper 2 Offline
JEE Advanced 2015 Paper 1 Offline
JEE Advanced 2014 Paper 2 Offline
JEE Advanced 2014 Paper 1 Offline
JEE Advanced 2013 Paper 2 Offline
JEE Advanced 2013 Paper 1 Offline
IIT-JEE 2012 Paper 2 Offline
IIT-JEE 2012 Paper 1 Offline
IIT-JEE 2011 Paper 1 Offline
IIT-JEE 2011 Paper 2 Offline
IIT-JEE 2010 Paper 2 Offline
IIT-JEE 2010 Paper 1 Offline
IIT-JEE 2009 Paper 2 Offline
IIT-JEE 2009 Paper 1 Offline
IIT-JEE 2008 Paper 2 Offline
IIT-JEE 2008 Paper 1 Offline
IIT-JEE 2007
IIT-JEE 2007 Paper 2 Offline
IIT-JEE 2006
IIT-JEE 2006 Screening
IIT-JEE 2005 Screening
IIT-JEE 2005
IIT-JEE 2004
IIT-JEE 2004 Screening
IIT-JEE 2003
IIT-JEE 2003 Screening
IIT-JEE 2002
IIT-JEE 2002 Screening
IIT-JEE 2001
IIT-JEE 2001 Screening
IIT-JEE 2000 Screening
IIT-JEE 2000
IIT-JEE 1999 Screening
IIT-JEE 1999
IIT-JEE 1998
IIT-JEE 1998 Screening
IIT-JEE 1997
IIT-JEE 1996
IIT-JEE 1995 Screening
IIT-JEE 1995
IIT-JEE 1994
IIT-JEE 1993
IIT-JEE 1992
IIT-JEE 1991
IIT-JEE 1990
IIT-JEE 1989
IIT-JEE 1988
IIT-JEE 1987
IIT-JEE 1986
IIT-JEE 1985
IIT-JEE 1984
IIT-JEE 1983
IIT-JEE 1982
IIT-JEE 1981
IIT-JEE 1980
IIT-JEE 1979
IIT-JEE 1978
JEE Advanced
Papers
2020
2019
2018
2017
2016
1997
1996
1994
1993
1992
1991
1990
1989
1988
1987
1986
1985
1984
1983
1982
1981
1980
1979
1978