The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

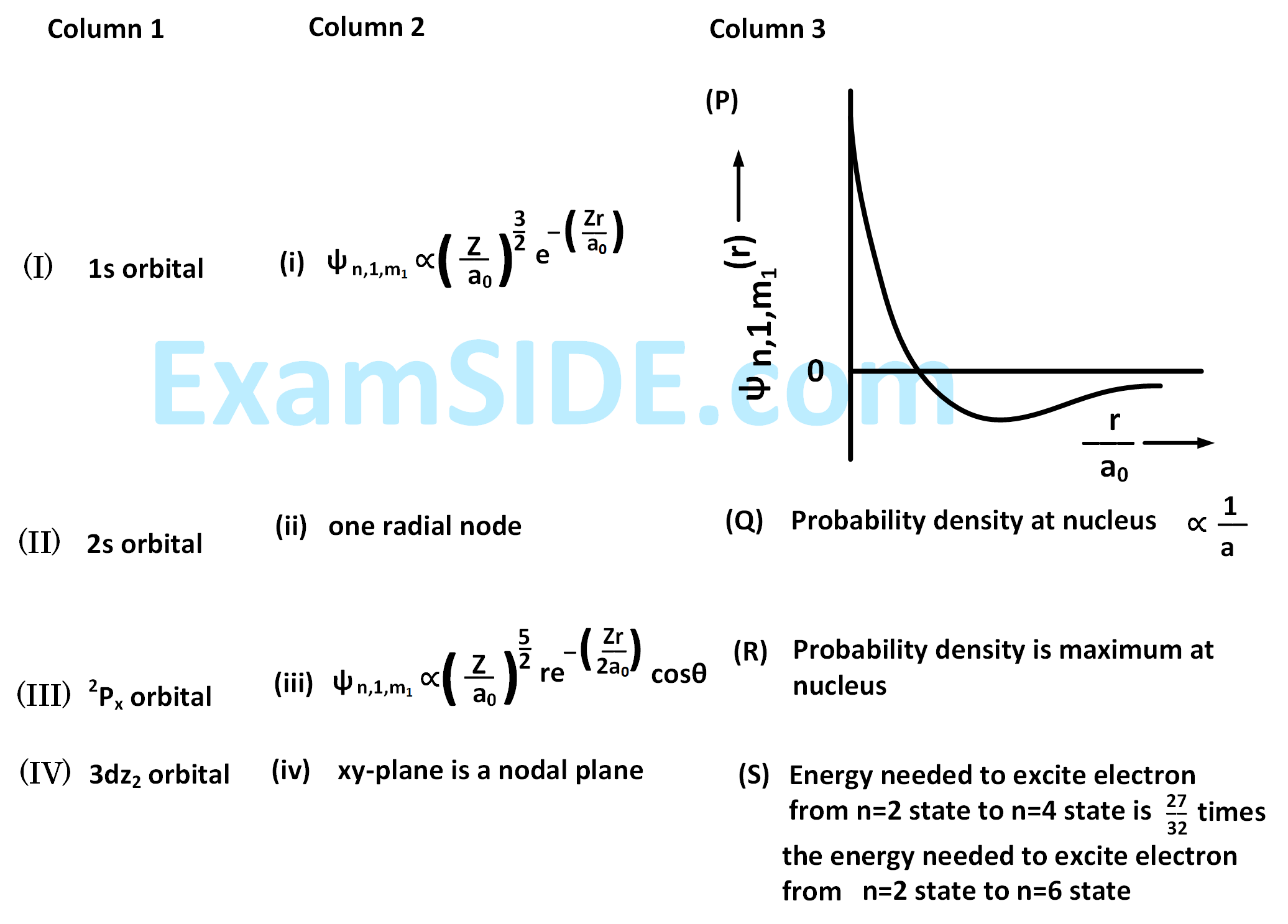
For hydrogen atom, the only CORRECT combination is :

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

For the given orbital in Column 1, the only CORRECT combination for any hydrogen-like species is :

Let X and Y be two events such that $$P(X) = {1 \over 3}$$, $$P(X|Y) = {1 \over 2}$$ and $$P(Y|X) = {2 \over 5}$$. Then

Let f : R $$ \to $$ (0, 1) be a continuous function. Then, which of the following function(s) has (have) the value zero at some point in the interval (0, 1) ?