1
JEE Advanced 2023 Paper 2 Online
MCQ (Single Correct Answer)
+3
-1

Young's modulus of elasticity $Y$ is expressed in terms of three derived quantities, namely, the gravitational constant $G$, Planck's constant $h$ and the speed of light $c$, as $Y=c^\alpha h^\beta G^\gamma$. Which of the following is the correct option?
2
JEE Advanced 2022 Paper 2 Online
MCQ (Single Correct Answer)
+3
-1

Area of the cross-section of a wire is measured using a screw gauge. The pitch of the main scale is $0.5 \mathrm{~mm}$. The circular scale has 100 divisions and for one full rotation of the circular scale, the main scale shifts by two divisions. The measured readings are listed below.
| Measurement condition | Main scale reading | Circular scale reading |
|---|---|---|
| Two arms of gauge touching each other without wire |
0 division | 4 divisions |
| Attempt-1: With wire | 4 divisions | 20 divisions |
| Attempt-2: With wire | 4 divisions | 16 divisions |
What are the diameter and cross-sectional area of the wire measured using the screw gauge?
3
JEE Advanced 2021 Paper 1 Online
MCQ (Single Correct Answer)
+3
-1

The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is
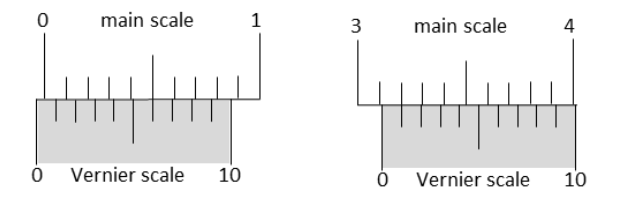

4
JEE Advanced 2018 Paper 1 Offline
MCQ (Single Correct Answer)
+3
-1

If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
Questions Asked from Units & Measurements (MCQ (Single Correct Answer))
Number in Brackets after Paper Indicates No. of Questions
JEE Advanced 2025 Paper 2 Online (1)
JEE Advanced 2025 Paper 1 Online (1)
JEE Advanced 2024 Paper 1 Online (1)
JEE Advanced 2023 Paper 2 Online (1)
JEE Advanced 2022 Paper 2 Online (1)
JEE Advanced 2021 Paper 1 Online (1)
JEE Advanced 2018 Paper 1 Offline (2)
JEE Advanced 2017 Paper 2 Offline (1)
JEE Advanced 2016 Paper 2 Offline (1)
JEE Advanced 2013 Paper 2 Offline (1)
JEE Advanced 2013 Paper 1 Offline (1)
IIT-JEE 2012 Paper 1 Offline (1)
IIT-JEE 2011 Paper 1 Offline (1)
IIT-JEE 2011 Paper 2 Offline (1)
IIT-JEE 2010 Paper 2 Offline (1)
IIT-JEE 2008 Paper 1 Offline (1)
IIT-JEE 2007 (1)
IIT-JEE 2007 Paper 2 Offline (1)
IIT-JEE 2006 (2)
IIT-JEE 2005 Screening (1)
IIT-JEE 2004 Screening (2)
IIT-JEE 2003 Screening (1)
IIT-JEE 2001 Screening (1)
IIT-JEE 2000 Screening (1)
JEE Advanced Subjects
Physics
Mechanics
Units & Measurements Motion Laws of Motion Work Power & Energy Impulse & Momentum Rotational Motion Properties of Matter Heat and Thermodynamics Simple Harmonic Motion Waves Gravitation
Electricity
Electrostatics Current Electricity Capacitor Magnetism Electromagnetic Induction Alternating Current Electromagnetic Waves
Optics
Modern Physics
Chemistry
Physical Chemistry
Some Basic Concepts of Chemistry Structure of Atom Redox Reactions Gaseous State Chemical Equilibrium Ionic Equilibrium Solutions Thermodynamics Chemical Kinetics and Nuclear Chemistry Electrochemistry Solid State Surface Chemistry
Inorganic Chemistry
Periodic Table & Periodicity Chemical Bonding & Molecular Structure Isolation of Elements Hydrogen s-Block Elements p-Block Elements d and f Block Elements Coordination Compounds Salt Analysis
Organic Chemistry
Mathematics
Algebra
Quadratic Equation and Inequalities Sequences and Series Mathematical Induction and Binomial Theorem Matrices and Determinants Permutations and Combinations Probability Vector Algebra 3D Geometry Statistics Complex Numbers
Trigonometry
Coordinate Geometry
Calculus