
A light ray is incident on the surface of a sphere of refractive index $n$ at an angle of incidence $\theta_0$. The ray partially refracts into the sphere with angle of refraction $\phi_0$ and then partly reflects from the back surface. The reflected ray then emerges out of the sphere after a partial refraction. The total angle of deviation of the emergent ray with respect to the incident ray is $\alpha$. Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) If $n = 2$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (1) $30^\circ$ and $0^\circ$ |
| (Q) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (2) $60^\circ$ and $0^\circ$ |
| (R) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\phi_0$ will be | (3) $45^\circ$ and $0^\circ$ |
| (S) If $n = \sqrt{2}$ and $\theta_0 = 45^\circ$, then all the possible values of $\alpha$ will be | (4) $150^\circ$ |
| (5) $0^\circ$ |

List I contains four combinations of two lenses (1 and 2) whose focal lengths (in $\mathrm{cm}$ ) are indicated in the figures. In all cases, the object is placed $20 \mathrm{~cm}$ from the first lens on the left, and the distance between the two lenses is $5 \mathrm{~cm}$. List II contains the positions of the final images.
| List-I | List-II |
|---|---|
(I)  |
(P) Final image is formed at $7.5 \mathrm{~cm}$ on the right side of lens 2 . |
(II)  |
(Q) Final image is formed at $60.0 \mathrm{~cm}$ on the right side of lens 2 . |
(III)  |
(R) Final image is formed at $30.0 \mathrm{~cm}$ on the left side of lens $2 .$ |
(IV)  |
(S) Final image is formed at $6.0 \mathrm{~cm}$ on the right side of lens 2 . |
| (T) Final image is formed at $30.0 \mathrm{~cm}$ on the right side of lens 2 . |
Which one of the following options is correct?


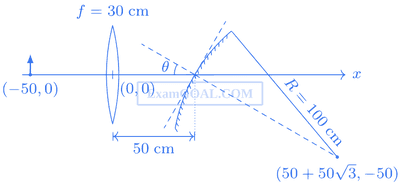
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x, y) at which the image is formed are