Area of the cross-section of a wire is measured using a screw gauge. The pitch of the main scale is $0.5 \mathrm{~mm}$. The circular scale has 100 divisions and for one full rotation of the circular scale, the main scale shifts by two divisions. The measured readings are listed below.

Measurement condition	Main scale reading	Circular scale reading
Two arms of gauge touching each other without wire	0 division	4 divisions
Attempt-1: With wire	4 divisions	20 divisions
Attempt-2: With wire	4 divisions	16 divisions

What are the diameter and cross-sectional area of the wire measured using the screw gauge?

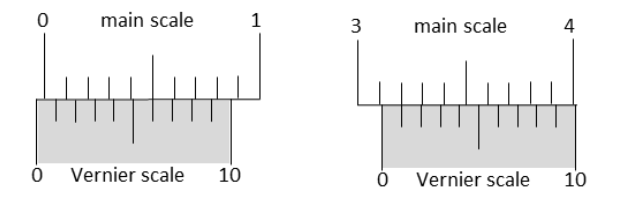
The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is

In electromagnetic theory, the electric and magnetic phenomena are related to each other. Therefore, the dimensions of electric and magnetic quantities must also be related to each other. In the questions below, $$[E]$$ and $$[B]$$ stand for dimensions of electric and magnetic fields respectively, while $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ stand for dimensions of the permittivity and permeability of free space respectively. $$\left[ L \right]$$ and $$\left[ T \right]$$ are dimensions of length and time respectively. All the quantities are given in $$SI$$ units.

The relation between $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ is

If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$

The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$

The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.

In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is