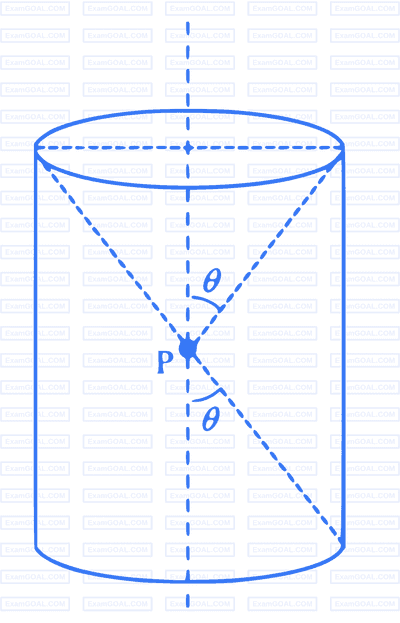
A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.

An infinitely long thin wire, having a uniform charge density per unit length of $5 \mathrm{nC} / \mathrm{m}$, is passing through a spherical shell of radius $1 \mathrm{~m}$, as shown in the figure. A $10 \mathrm{nC}$ charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points $\mathrm{P}$ and $\mathrm{R}$, in Volt, is ________.

[Given: In SI units $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$. Ignore the area pierced by the wire.]

A charge $q$ is surrounded by a closed surface consisting of an inverted cone of height $h$ and base radius $R$, and a hemisphere of radius $R$ as shown in the figure. The electric flux through the conical surface is $\frac{n q}{6 \epsilon_{0}}$ (in SI units). The value of $n$ is _______.

Two point charges $$-$$Q and +Q/$$\sqrt 3 $$ are placed in the xy-plane at the origin (0, 0) and a point (2, 0), respectively, as shown in the figure. This results in an equipotential circle of radius R and potential V = 0 in the xy-plane with its center at (b, 0). All lengths are measured in meters.



The value of R is __________ meter.