Column I

(A) GM_eM_s ,
G $$ \to $$ universal gravitational constant, M_e $$ \to $$ mass of the earth, M_s $$ \to $$ mass of the Sun

(B) $${{3RT} \over M}$$,
R $$ \to $$ universal gas constant, T $$ \to $$ absolute temperature, M $$ \to $$ molar mass

(C) $${{{F^2}} \over {{q^2}{B^2}}}$$ ,
F $$ \to $$ force, q $$ \to $$ charge, B $$ \to $$ magnetic field

(D) $${{G{M_e}} \over {{R_e}}}$$,
G $$ \to $$ universal gravitational constant, M_e $$ \to $$ mass of the earth, R_e $$ \to $$ radius of the earth

Column II

(p) (volt) (coulomb) (metre)

(q) (kilogram) (metre)³ (second)⁻²

(r) (meter)²(second)⁻²

(s) (farad) (volt)² (kg)⁻¹

A student performs an experiment to determine the Young's modulus of a wire, exactly 2 m long, by Searle's method. In a particular reading, the student measures the extension in the length of the wire to be 0.8 mm with an uncertainty of $$\pm0.05\;\mathrm{mm}$$ at a load of exactly 1.0 kg. The student also measures the diameter of the wire to be 0.4 mm with an uncertainty of $$\pm0.01\;\mathrm{mm}$$. Take g = 9.8 m/s² (exact). The Young's modulus obtained from the reading is

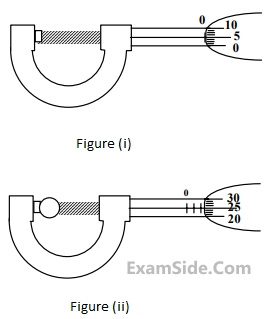
In a screw gauge, the zero of main scale coincides with the fifth division of circular scale in figure (i).The circular division of screw gauge is 50. It moves 0.5 mm on main scale in one rotation.The diameter of the ball in figure (ii) is