Some unknown material has a conductivity of $${10^{ 6}}$$ $$mho/m$$ and a permeability of $$4\pi \times {10^{ - 7}}\,\,\,\,\,H/m.$$ The skin depth for the material at $$1GHz$$ is

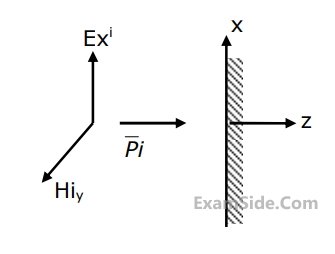
A plane wave is incident normally on a perfect conductor as shown in Fig. Here $$E_x^i,\,\,H_y^i$$ and $$\overrightarrow P {}^i$$ are electric field, magnetic field and Poynting vector respectively, for the incident wave. The reflected wave should have

A material is described by the following electrical parameters at a frequency of $$10$$ GHz is $$\sigma = {10^6}$$ mho/m, $$\mu = {\mu _0},$$ and $$ \in /{ \in _0} = 10.$$ The material at this frequency is considered to be $$\left( {{ \in _0} = {1 \over {36\,\,\pi }} \times {{10}^{ - 9}}\,\,F/m} \right)$$

The electric field component of a uniform plane electromagnetic wave propagating in the $$Y$$-direction in a lossless medium will satisfy the equation