All the springs in fig. (a), (b) and (c) are identical, each having force constant K each. Mass m is attached to each system. If $\mathrm{T}_a, \mathrm{~T}_b$ and $\mathrm{T}_{\mathrm{c}}$ are the time periods of oscillations of the three systems in fig. (a), (b) and (c) respectively, then

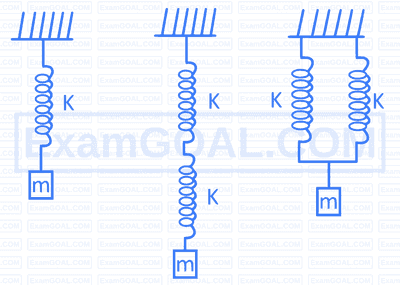
A point particle of mass 200 gram is executing S.H.M. of amplitude 0.2 m . When the particle passes through the mean position, its kinetic energy is $16 \times 10^{-3} \mathrm{~J}$. The equation of motion of this particle is (Initial phase of oscillation $=0^{\circ}$ )

A simple pendulum starts oscillating simple harmonically from its mean position ( $\mathrm{x}=0$ ) with amplitude ' $a$ ' and periodic time ' $T$ '. The magnitude of velocity of pendulum at $x=\frac{a}{2}$ is

A simple pendulum is suspended from ceiling of a lift when lift is at rest its period is ' T '. With what acceleration ' $a$ ' should lift be accelerated upward in order to reduce the period to ' $T$ '? (take ' g ' as acceleration due to gravity)