Electrostatics · Physics · MHT CET

$$ \text { The electric flux through the surface } $$

An electric dipole of length 2 cm is placed with its axis making an angle of $60^{\circ}$ to a uniform electric field of $10^{+5} \mathrm{~N} / \mathrm{C}$. If it experiences a torque of $9 \sqrt{3} \mathrm{Nm}$, the magnitude of the charge on the dipole is $\left(\sin 60^{\circ}=\frac{\sqrt{3}}{2}\right)$

A charge is uniformly distributed on the surface of a spherical rubber balloon. As it is blown up, the total electric flux coming out of the surface

The point charges $+\mathrm{q},-\mathrm{q},-\mathrm{q},+\mathrm{q},+\mathrm{Q}$ and -q are placed at the vertices of a regular hexagon ABCDEF as shown in figure. The electric field at the centre of hexagon ' $O$ ' due to the five charges at $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ and F is twice the electric field at centre ' O ' due to charge +Q at E alone. The value of $Q$ is

Out of the following statements which is NOT the characteristics of electric lines of force?

Charges of $2 \mu \mathrm{C}$ and $-3 \mu \mathrm{C}$ are placed at two points A and B separated by distance of 1 m . The distance of the point from $A$ where net potential is zero is

Assuming the drops to be spherical, 27 identical drops of mercury are charged simultaneously to the same potential of 20 volt. If all the charged drops are made to combine to form one big drop, then potential of big drop will be

Two equally charged small balls placed at a fixed distance experience a force ' $F$ '. A similar uncharged ball after touching one of them is placed at the middle point between the two balls. the force experienced by this ball is

Three charges $Q(-2 q)$ and $(-2 q)$ are placed at the vertices of an isosceles right angled triangle as shown in figure. The net electrostatic potential energy is zero if $Q$ is equal to

Two point charges $\mathrm{q}_1$ and $\mathrm{q}_2$ are ' $l$ ' distance apart. If one of the charges is doubled and distance between them is halved. The magnitude of force becomes $n$ times, where $n$ is

' $n$ ' identical small spherical drops of water, each of radius ' $r$ ' and charged to the same potential ' v ' are combined to form a big drop. The potential of a big drop is

Three charges ' $+3 q$ ', ' $Q$ ' and ' $+q$ ' are placed in a straight line of length ' $l$ ' at points at distances $0, \frac{l}{2}$ and $l$ respectively. The value of Q in order to have the net force on +q to be zero, $\mathrm{Q}=\mathrm{xq}$. The value of $x$ is

Two point charges $+10 \mu \mathrm{C}$ and $4 \mu \mathrm{C}$ are placed 10 cm apart in air. The work required to be done to bring them 2 cm closer is

$$ \left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \text { SI units }\right) $$

Out of the following molecules the one which represents the polar molecule is

The electric field intensity near a conducting surface having uniform surface charge density ' $\sigma$ ' is given by ( $\varepsilon_0=$ permittivity of free space)

A regular hexagon of side 6 cm has a charge of $2 \mu \mathrm{C}$ at each of its vertices, what is the potential at the centre of the hexagon?

$$ \left[\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \text { SI unit }\right] $$

Three equal charges are placed on the three corners of a square as shown below. If the magnitude of force between ' $\mathrm{q}_1$ ' and ' $\mathrm{q}_2$ ' is ' $\mathrm{F}_{12}$ ' and that between ' $\mathrm{q}_1$ ' and ' $\mathrm{q}_3$ ' is $\mathrm{F}_{13}$, then the ratio of $F_{13}$ to $F_{12}$ is

Three charges each of magnitude $3 \mu \mathrm{C}$, are placed on the vertices of an equilateral triangle of side 6 cm . The net potential energy of the system will be nearly $\left[\frac{1}{4 \pi \epsilon_0}=9 \times 10^9\right.$ SI unit $]$

Earth is assumed to be a charged conducting sphere having volume V and surface area A . The capacitance of the earth in free space is ( $\varepsilon_0=$ permittivity of free space)

A charge $\mathrm{Q} \mu \mathrm{C}$ is placed at the centre of a cube. The flux through two opposite faces of the cube is ( $\varepsilon_0=$ permittivity of free space)

Four charges $2 \mu \mathrm{C},-3 \mu \mathrm{C}, 4 \mu \mathrm{C},-4 \mu \mathrm{C}$ and $-1 \mu \mathrm{C}$ are enclosed by the Gaussian surface of radius 2 m . Net outward flux through the Gaussian surface is (in $\mu \mathrm{V}-\mathrm{m}$ ) [ $\varepsilon_0=$ permittivity of free space]

The electric field intensity on the surface of a solid charged sphere of radius $\mathbf{r}$ and volume charge density $\sigma$ is ( $\varepsilon_0=$ permittivity of free space)

The electric charges ' $+2 q$ ', ' $+2 q$ ', ' $-2 q$ ' and ' $-2 q$ ' are placed at the corners of square of side ' 2 L ' as shown in figure. The electric potential at point 'A', midway between the two charges ' $+2 q$ ' and ' $+2 q$ ' is

( $\varepsilon_0=$ permittivity of free space)

An electric dipole having each charge of magnitude $2 \mu \mathrm{C}$ is placed in an electric field of intensity $8 \times 10^{+4} \mathrm{~N} / \mathrm{C}$. If the maximum torque acting on the dipole is $4 \times 10^{-3} \mathrm{~N}-\mathrm{m}$, the length of the dipole is

Three concentric charged metallic spherical sheets $A, B$ and $C$ have radii $a, b, c$ potentials $V_A$, $\mathrm{V}_{\mathrm{B}}, \mathrm{V}_{\mathrm{C}}$ and charge densities $+\sigma,-\sigma$ and $+\sigma$ respectively. The value of potential $\mathrm{V}_{\mathrm{A}}$ is ( $\varepsilon_0=$ permittivity of free space)

Three point charges $+Q,+2 Q$ and $q$ are placed at the vertices of an equilateral triangle. The value of charge $q$ in terms of $Q$, so that electrical potential energy of the system is zero, is given by

A hollow cylinder has a charge of ' $q$ ' $C$ within it. If $\phi$ is the electric flux associated with the curved surface B, the flux linked with the plane surface A will be

A conducting sphere of radius ' R ' is given a charge ' $Q$ ' uniformly. The electric field and the electric potential at the centre of the sphere are respectively [ $\varepsilon_0=$ permittivity of free space]

' n ' small spherical drops of same size which are charged to ' $V$ ' volt each coalesce to form a single big drop. The potential of the big drop is

The electric potential ' V ' is given as a function of distance ' $x$ ' (metre) by $V=\left(4 x^2+8 x-3\right) V$. The value of electric field at $x=0.5 \mathrm{~m}$, in $\mathrm{V} / \mathrm{m}$ is

A uniformly charged conducting sphere of diameter 3.5 cm has a surface charge density of $20 \mu \mathrm{Cm}^{-2}$. The total electric flux leaving the surface of the sphere is nearly [permittivity of free space, $\varepsilon_0=8.85 \times 10^{-12} \mathrm{SI}$ unit]

A charged particle of mass ' $m$ ' and charge ' $q$ ' is at rest. It is acce:lerated in a uniform electric field of intensity ' $E$ ' : for time ' $t$ '. The kinetic energy of the particles after time $t$ is

Two charges $\mathrm{q}_1=+6_{\mathrm{q}}$ and $\mathrm{q}_2=-3 \mathrm{q}$ placed as shown in figure. A proton is placed on x -axis away from $\mathrm{q}_2$. To remain proton in equilibrium, the distance between $\mathrm{q}_1$ and proton is

A hollow cylinder has charge ' $q$ ' $C$ within it. If ' $\phi$ ' is the electric flux associated with the curved

' $n$ ' small drops of same size are charged to ' $V$ ' volt each. If they coalesce to form a single large drop, then its potential will be

Two point charges $+8 q$ and $-2 q$ are located at $x=0$ and $x=\mathrm{L}$ respectively. The location of a point on the $x$-axis from the origin, at which the net electric field due to these two point charges is zero is

When the dielectric is placed in an external electric field, the electric field inside the dielectric is

Charges of $2 \mu \mathrm{C}$ and $-3 \mu \mathrm{C}$ are placed at two points A and B separated by 1 m . The distance of the point from A , where net potential is zero, is

Two point charges $+q_1$ and $q_2$ repel each other with a force of $100 \mathrm{~N} . q_1$ is increased by $10 \%$ and $q_2$ is decreased by $10 \%$. If they are kept at their original positions the change in the force of repulsion between them is

In an electric field due to charge $Q$, a charge $q$ moves from point A to B as shown in the figure. The work done is ( $\varepsilon_0=$ permittivity of free space)

If a unit positive charge is shifted from a region of low potential to a region of high potential, then the electric potential energy of the system

Two point charges $+8 q$ and $-2 q$ are located at $\mathrm{X}=0$ (origin) and $\mathrm{X}=\mathrm{L}$ respectively. The net electric field due to these two charges is zero at point $P$ on $X$-axis. The location of point $P$ from the origin is

Consider a long uniformly charged cylinder having constant volume charge density ' $\lambda$ ' and radius ' $R$ '. A Gaussian surface is in the form of a cylinder of radius ' $r$ ' such that vertical axis of both the cylinders coincide. For a point inside the cylinder $(r< R)$, electric field is directly proportional to

An electric dipole will have minimum potential energy when it subtends an angle

$$\left[\begin{array}{l} \cos 0^{\circ}=1 \\ \sin 0^{\circ}=0 \end{array}\right]\left[\begin{array}{l} \cos 90^{\circ}=0 \\ \cos \pi=-1 \end{array}\right]$$

A particle ' $A$ ' has charge ' $+q$ ' and a particle ' $B$ ' has charge ' $+4 q$ '. Each has same mass ' $m$ '. When they are allowed to fall from rest through the same potential, the ratio of their speeds will become (particle A to particle B)

$A$ sphere ' $A$ ' of radius ' $R$ ' has a charge ' $Q$ ' on it. The field at point B outside the sphere is ' $E$ '. Now another sphere of radius ' $2 R$ ' having a charge ' $-2 Q$ ' is placed at B. The total field at the point midway between A and B due to both the spheres is

The point charges $+\mathrm{q},-\mathrm{q},-\mathrm{q},+\mathrm{q},+\mathrm{Q}$ and -q are placed at the vertices of a regular hexagon ABCDEF as shown in figure. The electric field at the centre of hexagon ' $O$ ' due to the five charges at $A, B, C, D$ and $F$ is thrice the electric field at centre ' $O$ ' due to charge +Q at E alone. The value of Q is

A small particle carrying a negative charge of $1.6 \times 10^{-19} \mathrm{C}$ is suspended in equilibrium between two horizontal metal plates 8 cm apart having a potential difference of 980 V across them. The mass of the particle is $\left[\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^2\right]$

Charges $3 \mathrm{Q}, \mathrm{q}$ and Q are placed along x -axis at positions $\mathrm{x}=0, \mathrm{x}=\frac{1}{3}$ and $\mathrm{x}=1$ respectively. When the force on charge Q is zero, the value of $q$ is

If a unit charge is taken from one point to another point over an equipotential surface, then

Two point charges $\mathrm{q}_1=6 \mu \mathrm{C}$ and $\mathrm{q}_2=4 \mu \mathrm{C}$ are kept at points $A$ and $B$ in air where $A B=10 \mathrm{~cm}$. What is the increase in potential energy of the system when $\mathrm{q}_2$ is moved towards $\mathrm{q}_1$ by 2 cm ?

$$\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \text { SI units }\right)$$

Two point charges $(A$ and $B)+4 q$ and $-4 q$ are placed along a line separated by a distance I '. Force acting between them is F. If $25 \%$ of charge from point $A$ is transferred to that at point B , the force between the charges now becomes

The electric potential at a point on the axis of an electric dipole is proportional to [r = distance between centre of the electric dipole and the point]

Four electric charges $+\mathrm{q},+\mathrm{q},-\mathrm{q}$ and -q are placed in order at the corners of a square of side 2 L. The electric potential at point midway between the two positive charges is

Two point charges +10 q and -4 q are located at $\mathrm{x}=0$ and $\mathrm{x}=\mathrm{L}$ respectively. What is the location of a point on the $x$-axis from the origin, which the net electric field due to these two point charges is zero?( $r=$ required distance$)$

The van de Graaff Generator is not based on

The electric flux over a sphere of radius ' $r$ ' is ' $\phi$ '. If the radius of the sphere is doubled without changing the charge, the flux will be

If the electric flux entering and leaving an enclosed surface is $\phi_1$ and $\phi_2$ then charge enclosed in the surface is ($\varepsilon_0=$ permittivity of free space)

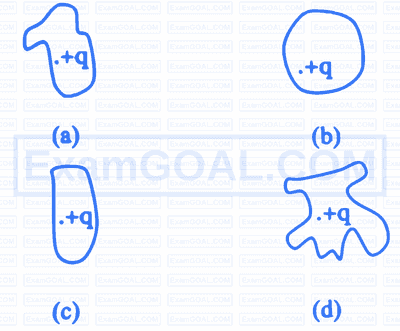
Two surfaces A and B are enclosing the charges as shown below. The total normal electric induction (T.N.E.I) through the surfaces A and B are respectively.

A spherical rubber balloon carries a charge, uniformly distributed over the surface. As the balloon is blown up and increases in size, the total electric flux coming out the surface

If a $10 \mu \mathrm{C}$ charge exists at the centre of a square, the work done in moving a $2 \mu \mathrm{C}$ point charge from corner A to corner B of a square ABCD is

If the electric flux entering and leaving an enclosed surface are $\phi_1$ and $\phi_2$ respectively, the electric charge inside the surface will be

An electron of mass ' $m$ ' and charge ' $q$ ' is accelerated from rest in a uniform electric field of intensity ' $E$ '. The velocity acquired by it as it travels a distance ' $l$ ' is ' $v$ '. The ratio $\frac{\mathrm{q}}{\mathrm{m}}$ in terms of $E, l$ and $v$ is

The electric potential at the centre of two concentric half rings of radii $R_1$ and $R_2$, having same linear charge density ' $\lambda$ ' is ($\varepsilon_0=$ permittivity of free space)

A metallic sphere ' A ' isolated from ground is charged to $+50 \mu \mathrm{C}$. This sphere is brought in contact with other isolated metallic sphere ' $B$ ' of half the radius of sphere ' $A$ '. Then the charge on the two isolated spheres A \& B are in the ratio

A regular hexagon of side 10 cm has a charge $1 \mu \mathrm{C}$ at each of its vertices. The potential at the centre of hexagon is $\left[\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9\right.$ SI unit $]$

Two charged particles each having charge ' $q$ ' and mass ' $m$ ' are held at rest while their separation is ' $r$ '. The speed of the particles when their separation is ' $\frac{\mathrm{r}}{2}$ ' will be ( $\varepsilon_0=$ permittivity of the medium)

A charge $+Q$ is placed at each of the diagonally opposite corners of a square. A charge -q is placed at each of the other diagonally opposite corners as shown. If the net electrical force on $+Q$ is zero, then $\frac{+Q}{-q}$ is equal to

Two equal point charges ' $q$ ' each exert a force ' $F$ ' on each other, when they are placed distance ' $x$ ' apart in air. When the same charges are placed distance ' $y$ ' apart in a medium of dielectric constant ' $k$ ', they exert the same force. The ratio of distance ' $y$ ' to ' $x$ ' is equal to

Three charges $2 q,-q$ and $-q$ are located at the vertices of an equilateral triangle. At the centre of the triangle

An electric dipole of moment $\overrightarrow{\mathrm{p}}$ is lying along a uniform electric field $\overrightarrow{\mathrm{E}}$. The work done in rotating the dipole through $\frac{\pi^{\mathrm{c}}}{3}$ is $\left[\sin 30^{\circ}=\cos 60^{\circ}=0 \cdot 5, \cos 30^{\circ}=\sin 60^{\circ}=\sqrt{3} / 2\right]$

Which of the following statement is correct?

Four point charges each +q is placed on the circumference of a circle of diameter 2 d in such a way that they form a square. The potential at the centre is proportional to

90 J of work is done to move an electric charge of magnitude 3 C from a place A , where potential is -10 V to another place B , where potential is ' $\mathrm{V}_1$ ' volt. The value of $\mathrm{V}_1$ is

Three charges are placed at the vertices of an equilateral triangle as shown in the figure. For what value of charge ' $Q$ ', the electrostatic potential energy of the system is zero?

A uniformly charged conducting sphere of diameter 14 cm has surface charge density of $40 \mu \mathrm{Cm}^{-2}$. The total electric flux leaving the surface of the sphere is nearly (Permittivity of free space $=8.85 \times 10^{-12}$ SI unit)

The electrostatic potential inside a charged spherical ball is given by $\mathrm{V}=\mathrm{ar}^2+\mathrm{b}$ where ' r ' is the distance from its centre and ' $a$ ' and ' $b$ ' are constants. The volume charge density of the ball is [ $\varepsilon_0=$ permittivity of free space $]$

A charge $$17.7 \times 10^{-4} \mathrm{C}$$ is distributed uniformly over a large sheet of area $$200 \mathrm{~m}^2$$. The electric field intensity at a distance $$20 \mathrm{~cm}$$ from it in air will be $$\left[\varepsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 / \mathrm{Nm}^2\right]$$

If $$\mathrm{E}_{\mathrm{a}}$$ and $$\mathrm{E}_{\mathrm{q}}$$ represent the electric field intensity due to a short dipole at a point on its axial line and on the equatorial line at the same distance '$$r$$' from the centre of the dipole, then

The electric field intensity on the surface of a solid charged sphere of radius '$$r$$' and volume charge density '$$\rho$$' is ($$\varepsilon_0=$$ permittivity of free space)

A uniformly charged semicircular arc of radius '$$r$$' has linear charge density '$$\lambda$$'. The electric field at its centre is ( $$\varepsilon_0=$$ permittivity of free space)

A conducting sphere of radius $$0.1 \mathrm{~m}$$ has uniform charge density $$1.8 \mu \mathrm{C} / \mathrm{m}^2$$ on its surface. The electric field in free space at radial distance $$0.2 \mathrm{~m}$$ from a point on the surface is ( $$\varepsilon_0=$$ permittivity of free space)

The work done in rotating a dipole placed parallel to the electric field through $$180^{\circ}$$ is W. So, the work done in rotating it through $$60^{\circ}$$ is $$\left(\cos 0^{\circ}=1, \cos 60^{\circ}=\frac{1}{2}, \cos 180^{\circ}=-1\right)$$

In the electric field due to a charge $$Q$$, a charge $$q$$ moves from point $$A$$ to $$B$$. The work done is ( $$\varepsilon_0=$$ permittivity of vacuum)

Which of the following statements is 'WRONG' for the conductors?

A charged spherical conductor of radius '$$R$$' is connected momentarily to another uncharged spherical conductor of radius '$$r$$' by means of a thin conducting wire, then the ratio of the surface charge density of the first to the second conductor is

If the magnitude of intensity of electric field at a distance '$$r_1$$' on an axial line and at a distance '$$r_2$$' on an equatorial line due to a given short dipole are equal, then $$r_1: r_2$$, is

Three charges each of value $$+q$$ are placed at the corners of an isosceles triangle $$\mathrm{ABC}$$ of sides $$\mathrm{AB}$$ and $$\mathrm{AC}$$ each equal to $$2 \mathrm{a}$$. The mid points of $$A B$$ and $$A C$$ are $$D$$ and $$E$$ respectively. The work done in taking a charge $$Q$$ from $$D$$ to $$E$$ is ( $$\varepsilon_0=$$ permittivity of free space)

Select the correct statement from the following.

Two point charges '$$q 1$$' and '$$q 2$$' are separated by a distance '$$d$$'. What is the increase in potential energy of the system when '$$q 2$$' is moved towards '$$q 1$$' by a distance '$$\mathrm{x}$$' ? $$(x < d)(\frac{1}{4 \pi \varepsilon_0}=K$$, constant)

Three point charges $$\mathrm{+Q,+2q}$$ and $$+\mathrm{q}$$ are placed at the vertices of a right angled isosceles triangle. The net electrostatic potential energy of the configuration is zero, if $$Q$$ is equal to

Two electric dipoles of moment $$\mathrm{P}$$ and $$27 \mathrm{P}$$ are placed on a line with their centres $$24 \mathrm{~cm}$$ apart. Their dipole moments are in opposite direction. At which point the electric field will be zero between the dipoles from the centre of dipole of moment P?

An electron of mass '$$\mathrm{m}$$' and charge '$$\mathrm{q}$$' is accelerated from rest in a uniform electric field of strength '$$E$$'. The velocity acquired by the electron, when it travels a distance '$$\mathrm{L}$$', is

Two positively charged identical spheres separated by a distance 'd' exert some force (F) on each other when they are kept in air. If both the spheres are immersed in a liquid of dielectric constant 5 , the force experienced by each is (All other parameters are unchanged.)

Two charges of equal magnitude '$$q$$' are placed in air at a distance '$$2 r$$' apart and third charge '$$-2 \mathrm{q}$$' is placed at mid point. The potential energy of the system is $$\left(\varepsilon_0=\right.$$ permittivity of free space)

An electron moving with velocity $$1.6 \times 10^7 \mathrm{~m} / \mathrm{s}$$ has wavelength of $$0.4 \mathop A\limits^o$$. The required accelerating voltage for the electron motion is [charge on electron $$=1.6 \times 10^{-19} \mathrm{C}$$, mass of electron $$=9 \times 10^{-31} \mathrm{~kg}$$ ]

Three point charges $$+\mathrm{q},+2 \mathrm{q}$$ and $$+\mathrm{Q}$$ are placed at the three vertices of an equilateral triangle. If the potential energy of the system of three charges is zero, the value of $$Q$$ in terms of $$q$$ is

The bob of a simple pendulum of length '$$L$$' has a mass '$$\mathrm{m}$$' and charge '$$\mathrm{q}$$'. The pendulum is suspended between the plates of a charged parallel plate capacitor. The direction of electric field is shown in figure. The period of oscillations of the simple pendulum is (acceleration due to gravity $$\mathrm{g}>\mathrm{qE} / \mathrm{m}$$ )

Assume that an electric field $$\mathrm{E}=30 \mathrm{x}^2 \hat{\mathrm{i}}$$ exists in space. If '$$\mathrm{V}_0$$' is the potential at the origin and '$$V_A$$' is the potential at $$x=2 \mathrm{~m}$$, then the potential difference $$\left(\mathrm{V}_{\mathrm{A}}-\mathrm{V}_0\right)$$ is

An electric dipole consisting of two opposite charges of $$2 \times 10^{-6} \mathrm{C}$$ separated by a distance of $$3 \mathrm{~cm}$$ placed in an electric field of $$2 \times 10^5 \mathrm{~N} / \mathrm{C}$$ then the maximum torque acting on dipole is

When a charge of $$3 ~\mathrm{C}$$ is placed in uniform electric field, it experiences a force of $$3000 \mathrm{~N}$$. Within this field, potential difference between two points separated by a distance of $$1 \mathrm{~cm}$$ is

The charges $$2 \mathrm{q},-\mathrm{q},-\mathrm{q}$$ are located at the vertices of an equilateral triangle. At the circumcentre of the triangle

A solid metallic sphere has a charge $$+3 Q$$. Concentric with this sphere is a conducting spherical shell having charge $$-\mathrm{Q}$$. The radius of the sphere is '$$A$$' and that of the spherical shell is '$$B$$'. $$(B > A)$$. The electric field at a distance '$$\mathrm{R}$$' $$(\mathrm{A} < \mathrm{R} < \mathrm{B})$$ from the centre is ( $$\varepsilon_0=$$ permittivity of vacuum)

If the radius of the spherical gaussian surface is increased then the electric flux due to a point charge enclosed by the surface

Three equal charges '$$\mathrm{q}_1$$', '$$^{\prime} \mathrm{q}_2$$' and '$$\mathrm{q}_3$$' are placed on the three corners of a square of side 'a'. If the force between $$\mathrm{q}_1$$ and $$\mathrm{q}_2$$ is '$$\mathrm{F}_{12}$$' and that between $$\mathrm{q}_1$$ and $$\mathrm{q}_3$$ is '$$\mathrm{F}_{13}$$', then the ratio of magnitudes $$\left(\frac{F_{12}}{F_{13}}\right)$$ is

Three charges each of $$+1 \mu \mathrm{C}$$ are placed at the corners of an equilateral triangle. If the repulsive force between any two charges is $$\mathrm{F}$$, then the net force on either charge will be [$$\cos 60^{\circ}=0.5$$]

Four electric charges $$+\mathrm{q},+\mathrm{q},-\mathrm{q}$$ and $$-\mathrm{q}$$ are placed in order at the corners of a square of side $$2 \mathrm{~L}$$. The electric potential at point midway between the two positive charges is

The electric field intensity on the surface of a charged solid sphere of radius '$$r$$' and volume charge dentiy '$$\rho$$' is given by ($$\epsilon_0=$$ permittivity of free space)

Let A, B and C be the three points in a uniform electric field $$\text { ( } \overrightarrow{\mathrm{E}})$$ as shown. The electric potential is

Two positive ions, each carrying a charge 'q' are separated by a distance 'd'. If 'F' is the force of repulsion between the ions, the number of electrons from each ion will be ($$\varepsilon$$ = charge on $$\varepsilon_k$$ = permittivity of free space)

Three charges $$-\mathrm{q}, \mathrm{Q}$$ and $$-\mathrm{q}$$ are placed at equal distances on a straight line. If the total potential energy of the system of three charges is zero then the ratio $$\frac{Q}{q}$$ is

Two point charges $$+3 \mu \mathrm{C}$$ and $$+8 \mu \mathrm{C}$$ repel each other with a force of $$40 \mathrm{~N}$$. If a charge of $$-5 \mu \mathrm{C}$$ is added to each of them, then force between them will become

In hydrogen atom an electron revolves around a proton (in nucleus) at a distance 'r' m. the intensity of electric field due to the proton at distance 'r' is $$5 \times 10^{11} \mathrm{NC}^{-1}$$, the magnitude of force between the electron and proton is [charge on electron $$=1.6 \times 10^{-19} \mathrm{C}$$]

Two charged metallic spheres are joined by a very thin metal wire. If the radius of the larger sphere is four times that of the smaller sphere, the electric field near the larger sphere is

A charged spherical conductor has radius '$$r$$'. The potential difference between its surface and 3 point at a distance '$$3 r$$' from the centre is '$$v$$' The electric intensity at a distance '$$3 r$$' from the centre of the conductor is

Two spherical conductors of radii $$4 \mathrm{~cm}$$ and $$5 \mathrm{~cm}$$ are charged to the same potential. If '$$\sigma_1$$' and '$$\sigma_2$$' be the respective values of the surface density of charge on the two conductors then the ratio $$\sigma_1: \sigma_2$$ is

An electron of mass '$$m$$' and charge '$$q$$' is accelerated from rest in a uniform electric field of strength '$$E$$'. The velocity acquired by the electron when it travels a distance '$$L$$' is

Two particles $$A$$ and $$B$$ having same mass have charge $$+q$$ and $$+4 q$$ respectively. When they are allowed to fall from rest through same electric potential difference, the ratio of their speeds '$$V_A$$' to '$$\mathrm{V}_{\mathrm{B}}$$' will become

A point charge $$\mathrm{Q}$$ is placed at the centre of the line joining two equal point charges $$+\mathrm{q}$$ and $$+\mathrm{q}$$. The value of $$Q$$ if the system of the charges is in equilibrium, is

When a piece of polythene is rubbed with wool, a negative charge of $$4 \times 10^{-7} \mathrm{C}$$ is developed on the polythene. The number of electrons transferred from wool to polythene is $$[e=1.6 \times\left.10^{-19} \mathrm{C}\right]$$

A hollow metal sphere has a radius 'r'. The potential difference between a point on its surface and at a point at a distance '3r' from its centre is 'V'. The electric intensity at the distance '3r' from the centre of the sphere will be :

'$$\mathrm{F}$$' is the force between the two identical charged particles placed at a distance '$$\mathrm{Y}$$' from each other. If the distance between the charges is reduced to half the previous distance then force between them becomes

A uniformly charged semicircular arc of radius '$$r$$' has linear charge density $$(\lambda)$$, is the electric field at its centre? ( $$\in_0=$$ permittivity of free space)

A hollow charged metal sphere has radius 'R'. If the potential difference between its surface and a point at a distance '5 R' from the centre is $$\mathrm{V}$$, then magnitude of electric field Intensity at a distance '5R' from the centre of sphere is

An electric dipole having dipole moment $$\mathrm{P}=\mathrm{q} \times 2 \ell$$ is placed in a uniform electric field '$$\mathrm{E}$$'. The dipole moment is along the direction of the field. The force acting on it and its potential energy are respectively

A uniformly charged half ring of a radius ' $R$ ' has linear charge density '$$\sigma$$'. The electric potential at the centre of the half ring is ( $$\epsilon_0=$$ permittivity of free space)

A spherical conducting shell of inner radius 'r$$_1$$' and outer radius 'r$$_2$$' has a charge 'Q'. A charge $$-$$q is placed at the centre of the shell. The surface charge density on the inner and outer surface of the shell will be

A charge of magnitude '2e' and mass '4m' is moving in an electric field $$\overrightarrow E $$. The acceleration imparted to the above charge is

Van de Graaff generator produces

A spherical rubber balloon carries a charge, uniformly distributed over the surface. As the balloon is blown up and increases in size, the total electric flux coming out of the surface

Surface density of charge on a charged conducting sphere of radius $$R$$ in terms of electric field intensity $$E$$ at a distance $$r$$ in free space is ($$r>R, \varepsilon_0=$$ permittivity of free space)

A charged conductor produces an electric field of intensity $10^3 \mathrm{~V} / \mathrm{m}$ just outside its surface in vacuum. Then, it produces the electric field of intensity E just outside its surface, when it is placed in a medium of dielectric constant 4. The value of $E$ will be

Which of the following is the dimensional formula for electric polarisation?

Which of the following molecules is a polar molecule?