Dual Nature of Radiation · Physics · MHT CET

A photosensitive surface has work function $\phi$. If photon of energy $3 \phi$ falls on this surface, the electron comes out with maximum velocity of $4 \times 10^6 \mathrm{~m} / \mathrm{s}$ When photon energy is increased to $7 \phi$ then maximum velocity of photoelectron will be

Energy of the incident photons on the metal surface is initially 4 W and then 6 W where $W$ is the work function of that metal. The ratio of velocities of emitted photoelectrons is

Let $E_c$ and $E_p$ represents kinetic energy of electron and photon respectively. If de-Broglie wavelength of a photon is twice the de-Broglie wavelength of an electron then $E_p / E_c$ is (speed of electron $=\mathrm{C} / 100$ where C is the velocity of light)

The graph shows the variation of photocurrent with anode potential for four different radiations. Let $\mathrm{I}_{\mathrm{a}}, \mathrm{I}_{\mathrm{b}}, \mathrm{I}_{\mathrm{c}}$ and $\mathrm{I}_{\mathrm{d}}$ are intensities and $\mathrm{f}_{\mathrm{a}}, \mathrm{f}_{\mathrm{b}}, \mathrm{f}_{\mathrm{c}}$ and $\mathrm{f}_{\mathrm{d}}$ be the frequencies for the curves $\mathrm{a}, \mathrm{b}, \mathrm{c}$ and d respectively, then

The wavelength ' $\lambda$ ' of a photon and the deBroglie wavelength of an electron have same value. the ratio of kinetic energy of the electron to the energy of a photon is

( $\mathrm{m}=$ mass of electron, $\mathrm{c}=$ velocity of light, $\mathrm{h}=$ Planck's constant)

If the frequency of incident light in a photoelectric experiment is doubled, then stopping potential will

An electron of mass ' $m$ ' and charge ' $e$ ' initially at rest gets accelerated by a constant electric field ' E '. The rate of change of de-Broglie wavelength of the electron at time ' $t$ ' is

(Ignore relativistic effect)( $\mathrm{h}=$ Planck's constant)

If the electron in hydrogen atom jumps from third Bohr orbit to ground state directly and the difference between energies of the two states is radiated in the form of photons. If the work function of the material is 4.1 eV , then stopping potential is nearly

[Energy of electron in $n^{\text {th }}$ orbit $=\frac{-13 \cdot 6}{n^2} \mathrm{eV}$ ]

When a metal surface is illuminated by light of wavelength $\lambda_1$ and $\lambda_2$, the maximum velocities of photoelectrons ejected are V and 2 V respectively. The work function of the metal is ( $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ velocity of light, $\lambda_1>\lambda_2$ )

Graph shows variation of stopping potential with frequency of incident radiation on a metal plate. The value of Planck's constant is [ $\mathrm{e}=$ charge on photoelectron]

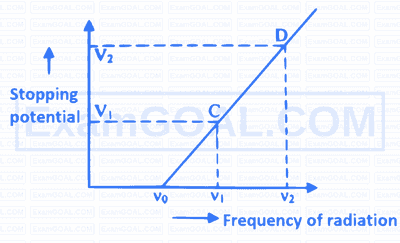
For two different photosensitive materials having work function $\phi$ and $2 \phi$ respectively, are illuminated with light of sufficient energy to emit electrons. If the graph of stopping potential versus frequency is drawn, for these two different photosensitive materials, the ratio of slope of graph for these two materials is

The energy that should be added to an electron to reduce its de-Broglie wavelength from $\lambda$ to $\frac{\lambda}{2}$ is $n$ times the initial energy. The value of ' $n$ ' is

When the electron orbiting in hydrogen atom goes from one orbit to another orbit (principal quantum number $=n$ ), the de-Broglie wavelength ( $\lambda$ ) associated with it is related to $n$ as

Photoelectric emission takes place from a certain metal at threshold frequency $v$. If the radiation of frequency $4 v$ is incident on the metal plate, the maximum velocity of the emitted photoelectrons will be ( $m=$ mass of photoelectron, $h=$ Planck's constant)

The de-Broglie wavelength of a neutron at $27^{\circ} \mathrm{C}$ is ' $\lambda_0$ '. What will be its wavelength at $927^{\circ} \mathrm{C}$ ?

When a photosensitive metal surface is illuminated with radiation of wavelength ' $\lambda_1$ ', the stopping potential is ' $\mathrm{V}_1$ '. If the same surface is illuminated with radiation of wavelength ' $3 \lambda_1$ ', the stopping potential is $\frac{\mathrm{V}_1}{6}$. The threshold wavelength for the photosensitive metal surface is

From photoelectric effect experiment, select the correct statement.

When photons of energies twice and thrice the work function of a metal are incident on the metal surface one after other, the maximum velocities of the photoelectrons emitted in the two cases are $V_1$ and $V_2$ respectively. The ratio $\mathrm{V}_1: \mathrm{V}_2$ is

When a light of wavelength $\lambda$ falls on the emitter of a photocell, maximum speed of emitted photoelectrons is V . If the incident wavelength is changed to $\frac{2 \lambda}{3}$, maximum speed of emitted photoelectrons will be :

The de-Broglie wavelength $(\lambda)$ of a particle

Photoelectric emission is observed from a metallic surface for frequencies $v_1$ and $v_2$ of the incident light rays $\left(v_1>v_2\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of $1: \mathrm{k}$, then the threshold frequency of metallic surface is

On a photosensitive material, when frequency of incident radiation is increased by $20 \%$, maximum kinetic energy of emitted photoelectrons increases from 0.4 eV to 0.7 eV . The work function of the material is

A light of wavelength $\lambda$ is incident on a photosensitive surface of negligible work function. The photoelectrons emitted from the surface have de-Broglie wavelength $\lambda_1$. Then ratio $\lambda: \lambda_1{ }^2$ is

( $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ velocity of light, $\mathrm{m}=$ mass of electron)

Light of wavelength ' $\lambda$ ' falls on a metal having work function $\frac{\mathrm{hc}}{\lambda_0}$. Photoelectric effect will take place only if ( $\lambda_0$ is the threshold wavelength)

A parallel beam of light is incident normally on a plane surface absorbing $50 \%$ of the light and reflecting the rest. If the incident beam carries 90 W of power, the force exerted by it on the surface is ( $\mathrm{C}=$ velocity of light in air $=3 \times 10^8 \mathrm{~m} / \mathrm{s}$ )

An electron accelerated by a potential difference ' $V$ ' has de-Broglie wavelength ' $\lambda$ '. If the electron is accelerated by a potential difference ' 9 V ', its de-Broglie wavelength will be

The maximum velocity of the photoelectrons emitted by a metal surface is $9 \times 10^5 \mathrm{~m} / \mathrm{s}$. The value of ratio of charge (e) to mass (m) of the photoelectron is $1.8 \times 10^{11} \mathrm{C} / \mathrm{kg}$. The value of stopping potential in volt is

Kinetic energy of a proton is equal to energy $E$ of a photon. Let ' $\lambda_1$ ' be the de-Broglie wavelength of proton and ' $\lambda_2$ ' be the wavelength of photon. If $\left(\frac{\lambda_1}{\lambda_2}\right) \propto E^n$ then the value of ' $n$ ' is

A point source of light is used in a photoelectric effect. If the source is removed farther from the emitting metal, then the stopping potential will

The figure shows the variation of photocurrent with anode potential for four different radiations. Let $\mathrm{I}_{\mathrm{a}}, \mathrm{I}_{\mathrm{b}}, \mathrm{I}_{\mathrm{c}}$ and $\mathrm{I}_{\mathrm{d}}$ be the intensities for the curves $a, b, c$ and $d$ respectively $\left[f_a, f_b, f_c\right.$ and $f_d$ are frequencies respectively]

When a certain metallic surface is illuminated with monochromatic light wavelength $\lambda$, the stopping potential for photoelectric current is $4 \mathrm{~V}_0$. When the same surface is illuminated with light of wavelength $3 \lambda$, the stopping potential is $\mathrm{V}_0$. The threshold wavelength for this surface for photoelectric effect is

The stopping potential as a function of frequency of incident radiation is plotted for two different photoelectric surfaces A and B. The graph shows that the work function of A is

Two photons having energies twice and thrice the work function of metal are incident one after another on the metal surface. Then the ratio of maximum velocities of the photoelectrons emitted in the two cases is respectively

Electrons are accelerated through a potential difference of 16 kV . If the potential difference is increased to 64 kV , then de-Broglie wavelength associated with electron will

In case of photoelectric effect, the graph of measured stopping potential $\left(\mathrm{V}_0\right)$ against frequency ' $v$ ' of incident light is a straight line. The slope of this line multiplied by the charge of electron (e) gives

A photoelectric surface is illuminated successively by monochromatic light of Wavelength $\lambda$ and $(\lambda / 3)$. If the maximum kinetic energy of the emitted photoelectrons in the second case is 4 times that in the first case, the work function of the surface of the material is $(\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ speed of light $)$

If the frequency of incident radiation $(\nu)$ is increased, keeping other factors constant, the stopping potential ( $\nu>\nu_0$, threshold frequency)

If the potential difference used to accelerate electrons is doubled. By what factor does the deBroglie wavelength $(\lambda)$ associated with the electrons change?

A photoelectric surface is illuminated successively by monochromatic light of wavelength ' $\lambda$ ' and $\left(\frac{\lambda}{2}\right)$. If the maximum kinetic energy of the emitted photoelectrons in the first case is one-fourth that in the second case, the work function of the surface of the material is ( $\mathrm{c}=$ speed of light, $\mathrm{h}=$ Planck's constant$)$

When a photosensitive surface is irradiated by lights of wavelengths ' $\lambda_1$ ' and ' $\lambda_2$ ', kinetic energies of the emitted photoelectrons is ' $E_1$ ' and ' $E_2$ ' respectively. The work function of the photosensitive surface is

In photoelectric effect, the photocurrent

If the potential difference used to accelerate electrons is increased four times, by what factor does the de-Broglie wavelength associated with the electrons change?

Using Einstein's photoelectric equation, the graph between kinetic energy of emitted photoelectrons and the frequency of incident radiation is shown correctly by graph

The figure shows the variation of photocurrent with anode potential for four different radiations. Let $f_a, f_b, f_c$ and $f_d$ be the frequencies for the curves $a, b, c$ and $d$ respectively

The gyromagnetic ratio and Bohr magneton are given respectively by [Given $\rightarrow \mathrm{e}=$ charge on electron, $\mathrm{m}=$ mass of electron, $\mathrm{h}=$ Planck's constant]

Two identical photocathodes receive light of frequencies ' $\mathrm{n}_1$ ' and ' $\mathrm{n}_2$ '. If the velocities of the emitted photoelectrons of mass ' $m$ ' are ' $\mathrm{V}_1$ ' and ' V , respectively, then ( $\mathrm{h}=$ Planck's constant )

The kinetic energy of an electron is increased by 2 times, then the de-Broglie wavelength associated with it changes by a factor.

A photosensitive metallic surface has work function $\phi$. If photon of energy $3 \phi$ falls on the surface, the electron comes out with a maximum velocity of $6 \times 10^6 \mathrm{~m} / \mathrm{s}$. When the photon energy is increased to $9 \phi$, then maximum velocity of photoelectrons will be

The threshold frequency of a metal is ' $F_0$ '. When light of frequency $2 F_0$ is incident on the metal plate, the maximum velocity of photoelectron is ' $\mathrm{V}_1$ '. When the frequency of incident radiation is increased to ' $5 \mathrm{~F}_0$ ', the maximum velocity of photoelectrons emitted is ' $V_2$ '. The ratio of $V_1$ to $V_2$ is

For a photosensitive material, work function is ' $\mathrm{W}_0$ ' and stopping potential is ' V '. The wavelength of incident radiation is ( $\mathrm{h}=$ Planck's constant, $c=$ velocity of light, $e=$ electronic charge)

The graph of stopping potential ' $\mathrm{V}_{\mathrm{s}}$ ' against frequency ' $v$ ' of incident radiation is plotted for two different metals ' X ' and ' Y ' as shown in graph. ' $\phi_x$ ' and ' $\phi_y$ ' are work functions of ' $x$ ' and ' $Y$ ' respectively then

The frequency of incident light falling on a photosensitive material is doubled, the K.E. of the emitted photoelectrons will be

When the electron orbiting in hydrogen atom in its ground state moves to the third excited state, the de-Broglie wavelength associated with it

The ratio of the wavelength of a photon of energy ' $E$ ' to that of the electron of same energy is ( $\mathrm{m}=$ mass of an electron, $\mathrm{c}=$ speed of light, $\mathrm{h}=$ Planck's constant)

When photons of energy hv fall on a photosensitive surface of work function $\mathrm{E}_0$, photoelectrons of maximum energy $k$ are emitted. If the frequency of radiation is doubled the maximum kinetic energy will be equal to ( $\mathrm{h}=$ Planck's constant)

The number of photoelectrons emitted for light of frequency $v$ (higher than the threshold frequency $\left(v_0\right)$ is proportional to

The stopping potential for a photelectric emission process is 10 V . The maximum kinetic energy of the electrons ejected in the process is [Charge on electron $\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}$ ]

When a metallic surface is illuminated with a radiation of wavelength ' $\lambda$ ', the stopping potential is ' $V$ '. If the same surface is illuminated with radiation of wavelength ' $3 \lambda$ ', the stopping potential is ' $\left(\frac{\mathrm{V}}{6}\right)$ '. The threshold wavelength for the surface is

The work function of metal ' $A$ ' and ' $B$ ' are in the ratio $1: 2$. If light of frequency ' $f$ ' and ' $2 f$ ' is incident on surface ' $A$ ' and ' $B$ ' respectively, then the ratio of kinetic energies of emitted photo electrons is

When radiation of wavelength '$$\lambda$$' is incident on a metallic surface, the stopping potential is 4.8 V. If the surface is illuminated with radiation of double the wavelength then the stopping potential becomes $$1.6 \mathrm{~V}$$. The threshold wavelength for the surface is

The de-Broglie wavelength $$(\lambda)$$ of a particle is related to its kinetic energy (E) as

Dual nature of light is exhibited by

When radiations of wavelength $$\lambda$$ is incident on a metallic surface the stopping potential required is $$4.8 \mathrm{~V}$$. If same surface is illuminated with radiations of double the wavelength, then required stopping potential becomes $$1.6 \mathrm{~V}$$, then the value of threshold wavelength for the surface is

When a light of wavelength $$300 \mathrm{~nm}$$ fall on a photoelectric emitter, photo electrons are emitted. For another emitter light of wavelength $$600 \mathrm{~nm}$$ is just sufficient for liberating photoelectrons. The ratio of the work function of the two emitters is

Light of frequency 1.5 times the threshold frequency is incident on photosensitive material. If the frequency is halved and intensity is doubled, the photocurrent becomes

Graph shows the variation of de-Broglie wavelength $$(\lambda)$$ versus $$\frac{1}{\sqrt{V}}$$ where '$$V$$' is the accelerating potential for four particles A, B, C, D carrying same charge but of masses $$\mathrm{m_1, m_2, m_3, m_4}$$. Which on represents a particle of largest mass?

When an electron is accelerated through a potential '$$V$$', the de-Broglie wavelength associated with it is '$$4 \lambda$$'. When the accelerating potential is increased to $$4 \mathrm{~V}$$, its wavelength will be

Radiations of two photons having energies twice and five times the work function of metal are incident successively on metal surface. The ratio of the maximum velocity of photo electrons emitted in the two cases will be

When light of wavelength $$\lambda$$ is incident on a photosensitive surface the stopping potential is '$$\mathrm{V}$$'. When light of wavelength $$3 \lambda$$ is incident on same surface the stopping potential is $$\frac{\mathrm{V}}{6}$$. Then the threshold wavelength for the surface is

When a metallic surface is illuminated with radiation of wavelength '$$\lambda$$', the stopping potential is '$$\mathrm{V}$$'. If the same surface is illuminated with radiation of wavelength '$$2 \lambda$$', the stopping potential is '$$\left(\frac{\mathrm{v}}{4}\right)$$'. The threshold wavelength for the metallic surface is

A metal surface of work function $$1 \cdot 13 \mathrm{~eV}$$ is irradiated with light of wavelength $$310 \mathrm{~nm}$$. The retarding potential required to stop the escape of photoelectrons is [Take $$\frac{\mathrm{hc}}{\mathrm{e}}=1240 \times 10^{-9} \mathrm{SI}$$ units]

The maximum kinetic energies of photoelectrons emitted are $$\mathrm{K}_1$$ and $$\mathrm{K}_2$$ when lights of wavelengths $$\lambda_1$$ and $$\lambda_2$$ are incident on a metallic surface. If $$\lambda_1=3 \lambda_2$$ then

If the potential difference used to accelerate electrons is doubled, by what factor does the de-Broglie wavelength associated with electrons change?

The maximum kinetic energy of the photoelectrons varies

An electron accelerated through a potential difference '$$V_1$$' has a de-Broglie wavelength '$$\lambda$$'. When the potential is changed to '$$V_2$$' its de-Broglie wavelength increases by $$50 \%$$. The value of $$\left(\frac{\mathrm{V}_1}{\mathrm{~V}_2}\right)$$ is

Maximum kinetic energy of photon is '$$E$$' when wavelength of incident radiation is '$$\lambda$$'. If wavelength of incident radiations is reduced to $$\frac{\lambda}{3}$$ then energy of photon becomes four times. Then work function of the metal is

When photons of energies twice and thrice the work function of a metal are incident on the metal surface one after other, the maximum velocities of the photoelectrons emitted in the two cases are $$\mathrm{v}_1$$ and $$\mathrm{v}_2$$ respectively. The ratio $$\mathrm{v}_1: \mathrm{v}_2$$ is

When a certain metal surface is illuminated with light of frequency $$v$$, the stopping potential for photoelectric current is $$\mathrm{V}_0$$. When the same surface is illuminated by light of frequency $$\frac{v}{2}$$, the stopping potential is $$\frac{\mathrm{V}_0}{4}$$, the threshold frequency of photoelectric emission is

From a metallic surface photoelectric emission is observed for frequencies $$v_1$$ and $$v_2\left(v_1 > v_2\right)$$ of the incident light. The maximum values of the kinetic energy of the photoelectrons emitted in the two cases are in the ratio $$1: \mathrm{x}$$. Hence the threshold frequency of the metallic surface is

If the kinetic energy of a free electron doubles, it's de Broglie wavelength ($$\lambda$$) changes by a factor

A light of wavelength '$$\lambda$$' and intensity '$$\mathrm{I}$$' falls on photosensitive material. If '$$\mathrm{N}$$' photo electrons are emitted, each with kinetic energy 'E', then

In a photoelectric experiment, a graph of maximum kinetic energy $$(\mathrm{KE}_{\text {max }})$$ against the frequency of incident radiation (v) is plotted. If $$\mathrm{A}$$ and $$\mathrm{B}$$ are the intercepts on the $$\mathrm{X}$$ and $$\mathrm{Y}$$ axis respectively then the Planck's constant is given by

A photon has wavelength $$3 \mathrm{~nm}$$, then its momentum and energy respectively will be $$[\mathrm{h}=6.63 \times 10^{-34} \mathrm{Js}, \mathrm{c}=$$ velocity of light $$=3 \times 10^8 \mathrm{~m} / \mathrm{s}]$$

In photoelectric experiment keeping the frequency of incident radiation and accelerating potential fixed, if the intensity of incident light is increased,

de-Broglie wavelength associated with an electron accelerated through a potential difference '$$\mathrm{V}$$' is '$$\lambda$$'. When the accelerating potential is increased to '$$4 \mathrm{~V}$$', de-Broglie wavelength.

In photoelectric effect, the photo current

According to de-Broglie hypothesis if an electron of mass '$$m$$' is accelerated by potential difference '$$V$$', the associated wavelength is '$$\lambda$$'. When a proton of mass '$$\mathrm{M}$$' is accelerated through potential difference $$9 \mathrm{~V}$$, then the wavelength associated with it is

When wavelength of incident radiation on the metal surface is reduced from '$$\lambda_1$$' to '$$\lambda_2$$', the kinetic energy of emitted photoelectrons is tripled. The work function of metal [$$\mathrm{h}=$$ Plank's constant, $$\mathrm{c}=$$ velocity of light]

An electron of mass '$$m$$' and a photon have same energy '$$E$$'. The ratio of de-Broglie wavelength of electron to the wavelength of photon is $$(\mathrm{c}=$$ velocity of light)

When a photon enters glass from air, which one of the following quantity does not change?

The light of wavelength '$$\lambda$$' is incident on the surface of metal of work function $$\phi$$ and emits the electron. The maximum velocity of electron emitted is [$$\mathrm{m}=$$ mass of electron and $$\mathrm{h}=$$ Planck's constant, $$\mathrm{c}=$$ velocity of light]

Photons of energy $$10 \mathrm{~eV}$$ are incident on a photosensitive surface of threshold frequency $$2 \times 10^{15} \mathrm{~Hz}$$. The kinetic energy in $$\mathrm{eV}$$ of the photoelectrons emitted is

[Planck's constant $$\mathrm{h}=6.63 \times 10^{34} \mathrm{~Js}$$ ]

When a light of wavelength '$$\lambda$$' falls on the emitter of a photocells, maximum speed of emitted photoelectrons is '$$\mathrm{V}$$'. If the incident wavelength is changed to $$\frac{2 \lambda}{3}$$, maximum speed of emitted photoelectrons will be

Kinetic energy of a proton is equal to energy '$$E$$' of a photon. Let '$$\lambda_1$$' be the de-Broglie wavelength of proton and '$$\lambda_2$$' is the wavelength of photon. If $$\frac{\lambda_1}{\lambda_2} \alpha E^n$$, then the value of '$$n$$' is

The wave number of the last line of the Balmer series in the hydrogen spectrum will be $$\left(\right.$$ Rydberg's cons $$\left.\tan t, R=\frac{10^7}{\mathrm{~m}}\right)$$

Photoemission from metal surface takes place for frequencies '$$v_1$$' and '$$v_2$$' of incident rays $$\left(v_1>v_2\right)$$. Maximum kinetic energy of photoelectrons emitted is in the ratio $$1: \mathrm{K}$$. The threshold frequency of metallic surface is

A proton and alpha particle are accelerated through the same potential difference. The ratio of the de-Broglie wavelength of proton to that of alpha particle will be (mass of alpha particle is four times mass of proton.)

Light of frequency two times the threshold frequency is incident on photosensitive material. If the incident frequency is made $$\left(\frac{1}{3}\right)^{\text {rd }}$$ and intensity is doubled, then the photoelectric current will

On a photosensitive surface, if the intensity of incident radiation is increased, the stopping potential

What is the additional energy that should be supplied to a moving electron to reduce its de Broglie wavelength from $$1 \mathrm{~nm}$$ to $$0.5 \mathrm{~nm}$$ ?

Photoelectrons are emitted when photons of energy $$4.2 ~\mathrm{eV}$$ are incident on a photosensitive metallic sphere of radius $$10 \mathrm{~cm}$$ and work function $$2.4 ~\mathrm{eV}$$. The number of photoelectrons emitted before the emission is stopped is

$$\left[\frac{1}{4 \pi \epsilon_0}=9 \times 10^9\right.$$ SI unit; $$\left.\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}\right]$$

When light of wavelength '$$\lambda$$' is incident on a photosensitive surface, photons of power 'P' are emitted. The number of photon 'n' emitted in time 't' is [h = Planck's constant, c = velocity of light in vacuum]

When a photosensitive surface is irradiated by light of wavelengths '$$\lambda_1$$' and '$$\lambda_2$$', kinetic energies of emitted photoelectrons are 'E$$_1$$' and 'E$$_2$$' respectively. The work function of photosensitive surface is

The graph of stopping potential $V_s$ against frequency $v$ of incident radiation is plotted for two different metals $P$ and $Q$ as shown in the graph. $\phi_p$ and $\phi_Q$ are work-functions of $P$ and $Q$ respectively, then

If the maximum kinetic energy of emitted electrons in photoelectric effect is $3.2 \times 10^{-19} \mathrm{~J}$ and the work-function for metal is $6.63 \times 10^{-19} \mathrm{~J}$, then stopping potential and threshold wavelength respectively are

[Planck's constant, $h=6.63 \times 10^{34} \mathrm{~J}$-s]

[Velocity of light, $c=3 \times 10^8 \frac{\mathrm{~m}}{\mathrm{~s}}$ ]

[Charge on electron $=1.6 \times 10^{-19} \mathrm{C}$ ]

The light of wavelength $$\lambda$$ incident on the surface of metal having work function $$\phi$$ emits the electrons. The maximum velocity of electrons emitted is [ $$c=$$ velocity of light, $$h=$$ Planck's constant, $$m=$$ mass of electron]

The graph of kinetic energy against the frequency $$v$$ of incident light is as shown in the figure. The slope of the graph and intercept on $$X$$-axis respectively are

The maximum velocity of the photoelectron emitted by the metal surface is $$v$$. Charge and mass of the photoelectron is denoted by $$e$$ and $$m$$, respectively. The stopping potential in volt is

Energy of the incident photon on the metal surface is $$3 W$$ and then $$5 W$$, where $$W$$ is the work function for that metal. The ratio of velocities of emitted photoelectrons is

The stopping potential of the photoelectrons, from a photo cell is

When certain metal surface is illuminated with a light of wavelength $\lambda$, the stopping potential is $V$, When the same surface is illuminated by light of wavelength $2 \lambda$, the stopping potential is $\left(\frac{V}{3}\right)$. The threshold wavelength for the surface is

A metal surface is illuminated by light of given intensity and frequency to cause photoemission. If the intensity of illumination is reduced to one fourth of its original value then the maximum KE of the emitted photoelectrons would be

When photons of energy $h v$ fall on a metal plate of work function ' $W_0$ ', photoelectrons of maximum kinetic energy ' $K$ ' are ejected. If the frequency of the radiation is doubled, the maximum kinetic energy of the ejected photoelectrons will be

The maximum velocity of the photoelectron emitted by the metal surface is ' $v$ '. Charge and mass of the photoelectron is denoted by ' $e$ ' and ' $m$ ' respectively. The stopping potential in volt is