Current Electricity · Physics · MHT CET
MCQ (Single Correct Answer)
A 2.5 V battery is connected to a potentiometer wire. A cell of e.m.f. 1.08 V is balanced by the voltage drop across 2.16 m of wire. The length of the potentiometer wire is
In metre-bridge experiment the balance point is obtained if the gaps are closed by $2 \Omega$ and $3 \Omega$. A shunt of $\mathrm{x} \Omega$ is added to $3 \Omega$ resistor to shift the balance point by 22.5 cm . The value of x is
In the following circuit, current through ACB if each resistance $\mathrm{R}=4 \Omega$ is

Kirchhoff's voltage law and current law are based (respectively) on the conservation of
The potentiometer wire is 5 m long and potential difference of 4 V is maintained between the ends. The e.m.f. of the cell which balances against a length of 200 cm of the potentiometer wire is
Two batteries of e.m.f 4 V and 8 V with internal resistance $1 \Omega$ and $2 \Omega$ respectively are connected in a circuit with a resistance of $9 \Omega$ as shown in the figure. The current and potential difference between the points ' P ' and ' Q ' is $\mathrm{R}=9 \Omega$

With a resistance ' X ' connected in series with a galvanometer of resistance $100 \Omega$, it acts as a voltmeter of range $0-15 \mathrm{~V}$. To double the range, a resistance of $1500 \Omega$ is to be connected in series with ' X '. The value of ' X ' in ohm is
The current (I) drawn from the battery in the given circuit is

The value of the shunt resistance that allows $10 \%$ of the main current through the galvanometer of $99 \Omega$ is
The length of a potentiometer wire is ' $L$ '. A cell of e.m.f. ' $E$ ' is balanced at a length $\frac{L}{4}$ from the positive end of the wire. If the length of the original wire is increased by $\frac{\mathrm{L}}{3}$, then using the same cell null point is obtained at
Two cells of e.m.f.s $E_1$ and $E_2\left(E_1>E_2\right)$ are connected as shown in figure.
 When the potentiometer is connected between A and B , the balancing length of the potentiometer wire is 3.60 m . On connecting the potentiometer between A and C , the balancing length is 0.90 m . The ratio $E_1 / E_2$ is
When the potentiometer is connected between A and B , the balancing length of the potentiometer wire is 3.60 m . On connecting the potentiometer between A and C , the balancing length is 0.90 m . The ratio $E_1 / E_2$ is
The equivalent resistance of the following circuit when no current flows in the resistance of $5 \Omega$ is nearly

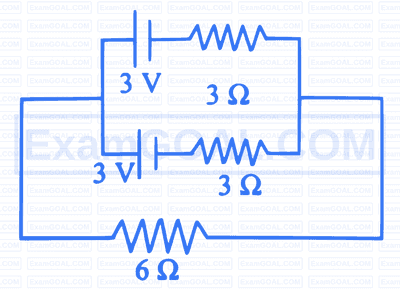
When cell of e.m.f. ' $E_1$ ' is connected to potentiometer wire, the balancing length is ' $l_l$ '. Another cell of e.m.f. ' $E_2$ ' $\left(E_1>E_2\right)$ is connected so that two cells oppose each other, the balancing length is ' $l_1$ '. The ratio $E_1: E_2$ is
In the given circuit, current flowing through the circuit is

The voltmeter has range 10 V and its internal resistance is $50 \Omega$. To increase the range of voltmeter to 15 V , the resistance which is to be connected is
In the given electrical network, the value of resistance ' $R$ ' when the current in the galvanometer will be zero, is
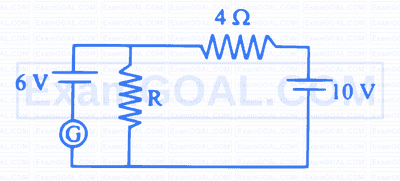
In the circuit shown in the figure, $P \neq R$. The reading of the galvanometer remains the same with switch ' $S$ ' open or closed. Then

If an ammeter is to be used in place of a galvanometer then we must connect
The length of a potentiometer wire is ' $L$ ' . A cell of e.m.f. $E$ is balanced at a length $\frac{L}{5}$ from the positive end of the wire. If the length of the wire is increased by $\frac{L}{2}$, the same cell will give balance point at distance ' $x$ '. The value of ' $x$ ' is
$$ \text { The value of current I in the given circuit is } $$

The reading of the ammeter in the following circuit is

If the length of the potentiometer wire is increased by keeping constant potential difference across the wire, then
Only $4 \%$ of the total current in the circuit passes through a galvanometer. If the resistance of the galvanometer is G , then the shunt resistance connected to the galvanometer is
The potential difference $\left(V_A-V_B\right)$ between the points A and B in the given figure is

A null point is obtained at 200 cm on potentiometer wire when cell in secondary circuit is shunted by $5 \Omega$. When a resistance of $15 \Omega$ is used for shunting, null point moves to 300 cm . The internal resistance of the cell is
To determine the internal resistance of a cell with potentiometer, when the cell is shunted by a resistance of $5 \Omega$ the balancing length is 250 cm . When the cell is shunted by $20 \Omega$, the balancing length of potentiometer wire is 400 cm . The internal resistance , of the cell is
Two cells $E_1$ and $E_2$ having equal e.m.f ' $E$ ' and internal resistances $r_1$ and $r_2\left(r_1>r_2\right)$ respectively are connected in series. This combination is connected to an external resistance ' R '. It is observed that the potential difference across the cell $E_1$ becomes zero. The value of $R$ will be
Two identical galvanometers are converted into an ammeter and into milliammeter. For the same current, the value of shunt of the ammeter as compared to that of milliammeter is
When a resistance of $200 \Omega$ is connected in series with a galvanometer of resistance ' $G$ ', its range is ' $V$ '. To triple its range, a resistance of $2000 \Omega$ is connected in series. The value of ' $G$ ' is
When a resistance of $100 \Omega$ is connected in series with a galvanometer of resistance G , its range is V . To double its range a resistance of $1000 \Omega$ is connected in series. The value of G is
The potential difference $\left(V_A-V_B\right)$ between the points A and B in the given part of the circuit

The figure shows currents in a part of electric circuit. Then current I is

A galvanometer may be converted into ammeter or a voltmeter. In which of the following cases the resistance of the device so obtained will be the largest?
A galvanometer has resistance $80 \Omega$ and it is shunted with resistance $20 \Omega$. If $20 \%$ of the main current flows through galvanometer, then what is the value of main current?
A cell balances against a length of 150 cm on a potentiometer wire when it is shunted by a resistance of $5 \Omega$. But when it is shunted by a resistance of $10 \Omega$, then balancing length increases by 25 cm . The balancing length when the cell is in an open circuit is
A battery of 6 V is connected to the ends of uniform wire 3 m long and of resistance $100 \Omega$. The difference of potential between two points 50 cm apart on the wire is
Kirchhoff's second law is based on the law of conservation of
In the following electrical network, the value of I is

The current drawn from the battery in the given network is (Internal resistance of the battery is negligible)

The potential difference $\left(V_A-V_B\right)$ between the points ' $A$ ' and ' $B$ ' in the given part of the circuit is

In an ammeter, $0.25 \%$ of main current passes through the galvanometer. If the resistance of the galvanometer is ' G ', the resistance of ammeter will be
In potentiometer experiment, cells of e.m.f. $E_1$ and $E_2$ are connected in series $\left(E_1>E_2\right)$ the balancing length is 80 cm of the wire. If the polarity of $E_2$ is reversed, the balancing length becomes 20 cm. The ratio $\mathrm{E}_1 / \mathrm{E}_2$ is
In the circuit, current flowing through the circuit is

Two identical galvanometers are converted into voltmeter and millivoltmeter. As compared to the series resistance of voltmeter, the series resistance of millivoltmeter will be
Potential difference between the points A and B is nearly

In the following circuit, the reading in the ammeter is

In an ammeter, $4 \%$ of the main current is passing through the galvanometer, If shunt resistance is $5 \Omega$, then resistance of galvanometer will be
When the two known resistance ' $R$ ' and ' $S$ ' are connected in the left and right gaps of a meter bridge respectively, the null point is found at a distance ' $l_1$ ' from the zero end of a meter bridge wire. An unknown resistance ' X ' is now connected in parallel with ' S ' and null point is found at a distance ' $l_2$ ' form zero end of meter bridge wire. The unknown resistance ' X ' is
In a Wheatstone's bridge, the resistances in four arms are as shown in the figure. The balancing condition of the bridge is

When a galvanometer is shunted by a resistance ' $s$ ', its current capacity increases ' $n$ ' times. If the same galvanometer is shunted by another resistance ' $s_1$ ', its capacity will increase to ' $n_1$ ' times original current. The value of ' $n_1$ ' is
In a meter bridge experiment, the balance point is obtained if the gaps are closed by $2 \Omega$ and $3 \Omega$. A shunt of $\mathrm{X} \Omega$ is added to $3 \Omega$ resistor to shift the null point by 22.5 cm. The value of ' $x$ ' is
A potentiometer wire of length 1 m is connected in series with $495 \Omega$ resistance and 2 V battery. If $0.2 \mathrm{mV} / \mathrm{cm}$ is the potential gradient, then the resistance of the potentiometer wire is
When a galvanometer is shunted by a resistance ' $S$ ', its current capacity increases ' $n$ ' times. If the same galvanometer is shunted by another resistance $\mathrm{S}^{\prime}$, its current capacity increases to $\mathrm{n}^{\prime}$. The value of $n^{\prime}$ in terms of $n, S$ and $S^{\prime}$ is
Resistances in the left gap and right gap of a meter bridge are $10 \Omega$ and $30 \Omega$ respectively. If the resistances in the two gaps are interchanged, the balance point will shift to right by
In the following circuit, a power of 50 watt is absorbed in the section AB of the circuit. The value of resistance ' $x$ ' is

The range of voltmeter of resistance ' $G$ ' $\Omega$ is ' $V$ ' volt. The resistance required to be connected in series with it in order to convert it into a voltmeter of range ' $n V$ ' volt, will be
When cell of E.M.F. ' $E_1$ ' is connected to potentiometer wire, the balancing length is $l_1$. Another cell of E.M.F. ' $E_2$ ' $\left(E_1>E_2\right)$ is connected so that two cells oppose each other, then the balancing length is $l_2$. The ratio $\mathrm{E}_1: \mathrm{E}_2$ is
The current flowing in a coil is 3 A and the power consumed is 108 W . If the a.c. source is of $120 \mathrm{~V}, 50 \mathrm{~Hz}$, the resistance in the circuit is
In the following circuit, the current flowing through zener diode is

In the following circuit, the current $\mathrm{I_2}$ is

A galvanometer of resistance ' $G$ ' is shunted by resistance of 'S' ohm. To keep the main current in the circuit unchanged the resistance to be put in series with Galvanometer is
The resistances in the left and right gap of a metre bridge are $40 \Omega$ and $60 \Omega$ respectively. When the bridge is balanced, the distance of the null point from the centre of the wire towards left is
When moving coil galvanometer (MCG) is converted into a voltmeter, the series resistance is '$$n$$' times the resistance of galvanometer. How many times that of MCG the voltmeter is now capable of measuring voltage?
In potentiometer experiment, the balancing length is $$8 \mathrm{~m}$$ when two cells $$E_1$$ and $$E_2$$ are joined in series. When two cells are connected in opposition the balancing length is $$4 \mathrm{~m}$$. The ratio of the e.m.f. of the two cells $$\left(\frac{E_1}{E_2}\right)$$ is
A wire of length $$3 \mathrm{~m}$$ connected in the left gap of a meter-bridge balances $$8 \Omega$$ resistance in the right gap at a point, which divides the bridge wire in the ratio $$3: 2$$. The length of the wire corresponding to resistance of $$1 \Omega$$ is
Five current carrying conductors meet at point $$\mathrm{P}$$. What is the magnitude and direction of the current in conductor $$\mathrm{PQ}$$?

A $$10 \mathrm{~m}$$ long wire of resistance $$20 \Omega$$ is connected in series with a battery of emf $$3 \mathrm{~V}$$ (negligible internal resistance) and a resistance of $$10 \Omega$$. The potential gradient along the wire is
Only $$4 \%$$ of the total current in the circuit passes through a galvanometer. If the resistance of the galvanometer is $$G$$, then the shunt resistance connected to the galvanometer is
Two cells $$E_1$$ and $$E_2$$ having equal EMF '$$E$$' and internal resistances $$r_1$$ and $$r_2\left(r_1>r_2\right)$$ respectively are connected in series. This combination is connected to an external resistance '$$R$$'. It is observed that the potential difference across the cell $$\mathrm{E}_1$$ becomes zero. The value of '$$R$$' will be
In a given meter bridge, the current flowing through $$40 \Omega$$ resistor is
A potentiometer wire of length $$4 \mathrm{~m}$$ and resistance $$5 ~\Omega$$ is connected in series with a resistance of $$992 ~\Omega$$ and a cell of e.m.f. $$4 \mathrm{~V}$$ with internal resistance $$3 ~\Omega$$. The length of $$0.75 \mathrm{~m}$$ on potentiometer wire balances the e.m.f. of
Two resistance $$\mathrm{X}$$ and $$\mathrm{Y}$$ are connected in the two gaps of a meterbridge and the null points is obtained at $$20 \mathrm{~cm}$$ from zero end. When the resistance of $$20 \Omega$$ is connected in series with the smaller of the two resistance $$\mathrm{X}$$ and $$\mathrm{Y}$$, the null point shifts to $$40 \mathrm{~cm}$$ from left end. The value of smaller resistance in ohm is
Resistance of a potentiometer wire is $$2 \Omega / \mathrm{m}$$. A cell of e.m.f. $$1.5 \mathrm{~V}$$ balances at $$300 \mathrm{~cm}$$. The current through the wire is
A potentiometer wire has length of $$5 \mathrm{~m}$$ and resistance of $$16 \Omega$$. The driving cell has an e.m.f. of $$5 \mathrm{~V}$$ and an internal resistance of $$4 \Omega$$. When the two cells of e.m.f.s $$1.3 \mathrm{~V}$$ and $$1.1 \mathrm{~V}$$ are connected so as to assist each other and then oppose each other, the balancing lengths are respectively
Two batteries, one of e.m.f. $$12 \mathrm{~V}$$ and internal resistance $$2 \Omega$$ and other of e.m.f. $$6 \mathrm{~V}$$ and internal resistance $$1 \Omega$$, are connected as shown in the figure. What will be the reading of the voltmeter 'V'?

Potential difference between the points P and Q is nearly

Potential difference between the points P and Q is nearly

In potentiometer experiments, two cells of e. m. f. '$$E_1$$' and '$$E_2$$' are connected in series $$\left(E_1>E_2\right)$$, the balancing length is $$64 \mathrm{~cm}$$ of the wire. If the polarity of $$E_2$$ is reversed, the balancing length becomes $$32 \mathrm{~cm}$$. The ratio $$\mathrm{E}_1 / \mathrm{E}_2$$ is
In meter bridge experiment, null point was obtained at a distance '$$l$$' from left end. The values of resistances in the left and right gap are doubled and then interchanged. The new position of the null point is
A galvanometer has resistance '$$\mathrm{G}$$' and range '$$\mathrm{V} g$$'. How much resistance is required to read voltage upto '$$\mathrm{V}$$' volt?
If only $$1 \%$$ of total current is passed through a galvanometer of resistance '$$G$$' then the resistance of the shunt is
A voltmeter of resistance $$150 \Omega$$ connected across a cell of e.m.f. $$3 \mathrm{~V}$$ reads $$2.5 \mathrm{~V}$$. What is the internal resistance of the cell?
A galvanometer of resistance $$20 ~\Omega$$ gives a deflection of 5 divisions when $$1 \mathrm{~mA}$$ current flows through it. The galvanometer scale has 50 divisions. To convert the galvanometer into a voltmeter of range 25 volt, we should connect a resistance of
Five current carrying conductors meet at a point '$$\mathrm{O}$$' as shown in figure. The magnitude and direction of the current in conductor '$$O P$$' is

A galvanometer of resistance $$\mathrm{G}$$ is shunted with a resistance of $$10 \%$$ of $$\mathrm{G}$$. The part of the total current that flows through the galvanometer is
In a meter bridge experiment null point is obtained at $$l \mathrm{~cm}$$ from the left end. If the meter bridge wire is replaced by a wire of same material but twice the area of across-section, then the null point is obtained at a distance
In the following network, the current through galvanometer will

A galvanometer of resistance $$200 \Omega$$ is to be converted into an ammeter. The value of shunt resistance which allows $$3 \%$$ of the mains current through the galvanometer is equal to (nearly)
The current drawn from the battery in the given network is (Internal resistance of the battery is negligible)

In the following electrical network, the value of 1 is

In a potentiometer experiement, when three cells $$\mathrm{A}, \mathrm{B}$$ and $$\mathrm{C}$$ are connected in series, the balancing length is found to be $$420 \mathrm{~cm}$$. If cells $$\mathrm{A}$$ and $$\mathrm{B}$$ are connected in series the balancing length is $$220 \mathrm{~cm}$$ and for cells $$\mathrm{B}$$ and $$\mathrm{C}$$ connected in series in balancing length is $$320 \mathrm{~cm}$$. The emf of cells $$\mathrm{A}, \mathrm{B}$$ and $$\mathrm{C}$$ are respectively in the ratio of
To determine the internal resistance of a cell by using a potentiometer, the null point is at $$1 \mathrm{~m}$$ when shunted by $$3 \Omega$$ resistance and at a length $$1.5 \mathrm{~m}$$, when cell is shunted by $$6 \Omega$$ resistance The internal resistance of the cell is
In the given circuit, the current in 8$$\Omega$$ resistance is 1.5 A. The total current (I) flowing in the circuit is

A balanced bridge is shown in the circuit diagram. The metre bridge wire has resistance $$1 \Omega \mathrm{m}^{-1}$$. The current drawn from the battery is (Internal resistance of battery is negligible)

In potentiometer experiment, cells of e.m.f. '$$E_1$$' and '$$E_2$$' are connected in series $$\left(E_1>E_2\right)$$ the balancing length is $$64 \mathrm{~cm}$$ of the wire. If the polarity of $$E_2$$ is reversed, the balancing length becomes $$32 \mathrm{~cm}$$. The ratio $$\frac{E_1}{E_2}$$ is
In a potentiometer experiment, the balancing length for a cell is $$240 \mathrm{~cm}$$. On shunting the cell with a resistance of $$2 \Omega$$, the balancing length becomes half the initial balancing length. The internal resistance of the cell is
Kirchhoff's current and voltage law are respectively based on the conservation of
In a wheatstone's bridge, three resistances $$\mathrm{P}, \mathrm{Q}$$ and $$\mathrm{R}$$ are connected in the three arms and the fourth arm is formed by two resistances $$S_1$$ and $$S_2$$ connected in parallel. The condition for the bridge to be balanced is
If a current flowing in a coil is reduced to half of its initial value, the relation between the new energy $$\left(E_2\right)$$ and the original energy $$\left(E_1\right)$$ stored in the coil will be
The Kirchhoff's current law and voltage law are respectively based upon the conservation of
A moving coil galvanometer is converted into an ammeter, reading upto $$0.04 \mathrm{~A}$$ by connecting a shunt of resistance '$$3 \mathrm{r}$$' across it and then into an ammeter reading upto $$0.8 \mathrm{~A}$$, when a shunt of resistance '$$r$$' is connected across it. What is the maximum current which can be sent through this galvanometer if no shunt is used?
A current through 1 $$\Omega$$ resistance in the following circuit is

In a meter bridge experiment, the balance point is obtained at length $$\ell_1 \mathrm{~cm}$$ from left end when resistances in the left gap and right gap are $$5 \Omega$$ and $$R \Omega$$ respectively. When the resistance $$R$$ is shunted with equal resistance, the new balance point is at $$1.6 \ell_1$$. The resitance $$R$$ in ohm is
Two wires '$$\mathrm{A}$$' and '$$\mathrm{B}$$' of equal length are connected in left and right gap respectively of meter bridge, null point is obtained at $$40 \mathrm{~cm}$$, from the left end. Diameters of the wires '$$A$$' and '$$B$$' are in the ratio $$3: 1$$ respectively, the ratio of specific resistance of 'A' to that of 'B' is
A galvanometer has resistance '$$\mathrm{G}$$' $$\Omega$$ and '$$\mathrm{I}_{\mathrm{g}}$$' is current flowing through it which produces full scale deflection. '$$\mathrm{S}_1$$' is the value of shunt which converts it into an ammeter of range 0 to '$$3 \mathrm{I}$$' and '$$\mathrm{S}_2$$' is the shunt value which converts it into an ammeter of range 0 to '$$4 \mathrm{I}$$', the ratio $$\mathrm{S}_2: \mathrm{S}_1$$ is
In potentiometer experiment, null point is obtained at a particular point for a cell on potentiometer wire '$$\mathrm{x}$$' cm long. If length of potentiometer wire is increased by few centimeter without changing the cell, the balancing length will [Driving source is not changed]
A galvanometer of resistance $$50 \Omega$$ is converted to an ammeter. After shunting, the effective resistance of ammeter is $$2.5 \Omega$$. The value of shunt is
Consider the circuit shown in the figure. The value of current 'I' is

A milliammeter of resistance $40 \Omega$ has a range $0-30 \mathrm{~mA}$. What will be the resistance used in series to convert it into voltmeter of range $0-15 \mathrm{~V}$ ?
Two cells having unknown emfs $E_1$ and $E_2$ $\left(E_1>E_2\right)$ are connected in potentiometer circuit, so as to assist each other. The null point obtained is at 490 cm from the higher potential end. When cell $E_2$ is connected, so as to oppose cell $E_1$, the null point is obtained at 90 cm from the same end. The ratio of the emfs of two cells $\left(\frac{E_1}{E_2}\right)$ is
A 10 m long wire of resistance $20 \Omega$ is connected in series with a battery of emf 3 V and a resistance of $10 \Omega$. The potential gradient along the wire in $\mathrm{V} / \mathrm{m}$ is
Two galvanometers $A$ and $B$ require currents of 4 mA and 7 mA , respectively to produce the same deflection of 20 divisions. If $S_A$ and $S_B$ are their sensitivities respectively, then
A circular coil of radius $$R$$ has a resistance of $$40 \Omega$$. Figure shows two points $$P$$ and $$Q$$ on the circumference separated by a distance $$\frac{\pi R}{2}$$ which are connected to a 16 V battery with internal resistance of $$0.5 \Omega$$. What is the value of current $$I$$ flowing through the circuit?

Which of the following instruments is not a direct reading instrument?
In conversion of moving coil galvanometer into an ammeter of required range, the resistance of ammeter, so formed is
[$$S=$$ shunt and $$G=$$ resistance of galvanometer]
An ammeter of resistance $$20 \Omega$$ gives full scale deflection, when $$1 \mathrm{~mA}$$ current flows through it. What is the maximum current that can be measured by connecting 4 resistors each of $$16 \Omega$$ in parallel with the ammeter?
Two wires $$A$$ and $$B$$ of equal lengths are connected in left and right gap of a meter bridge, null point is obtained at $$40 \mathrm{~cm}$$ from left end. Diameters of the wire $$A$$ and $$B$$ are in that ratio $$3: 1$$. The ratio of specific resistance of $$A$$ to the of $$B$$ is
A potentiometer wire is $$4 \mathrm{~m}$$ long and potential difference of $$3 \mathrm{~V}$$ is maintained between the ends. The emf of the cell, which balances against a length of $$100 \mathrm{~cm}$$ of the potentiometer wire is
A potentiometer wire has length $L$ For given cell of emf $E$, the balancing length is $\frac{L}{3}$ from the positive end of the wire. If the length of potentiometer wire is increased by $50 \%$, then for the same cell, the balance point is obtained at length
In the network shown cell E has internal resistance $r$ and the galvanometer shows zero deflection. If the cell is replaced by a new cell of emf $2 E$ and internal resistance $3 r$ keeping everything else identical, then

The range of an ammeter of resistance ' $G$ can be increased from ' $I$ ' to ' $nI$ ' by connecting
In the given electrical circuit, which one of the following equations is a correct equation?

With a resistance of ' $X$ ' in the left gap and resistance of $9 \Omega$ in the right gap of a meter bridge, the balance point is obtained at 40 cm from the left end. In what way and to which resistance $3 \Omega$ resistance be connected to obtain the balance at 50 cm from the left end?
In moving coil galvanometer, strong horse shoe magnet of concave shaped pole pieces is used to
For a metallic wire, the ratio of voltage to corresponding current is
A galvanometer has resistance of $100 \Omega$ and a current of 10 mA produces full scale deflection in it. The resistance to be connected in series, to get a voltmeter of range 50 volt is
The circuit in 1$$\Omega$$ resistor in the following circuit is
