A stone of mass ' m ' kg is tied to a string of length ' $L$ ' $m$ and moved in a vertical circle of radius 49 cm in a vertical plane. If it completes 30 revolutions per minute, the tension in the string when it is at the lowermost point is nearly [Take $\pi^2=10$ and acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ ]
A point mass ' $m$ ' attached at one end of a massless, inextensible string of length ' $l$ ' performs a vertical circular motion and the string rotates in vertical plane, as shown in the diagram. The increase in the centripetal acceleration of the point mass when it moves from point A to point C is
[ $\mathrm{g}=$ acceleration due to gravity.]

An inextensible string of length ' $l$ ' fixed at one end, carries a mass ' $m$ ' at the other end. If the string makes $\frac{1}{\pi}$ revolutions per second around the vertical axis through the fixed end, the tension in the string is [The string makes an angle $\theta$ with the vertical]
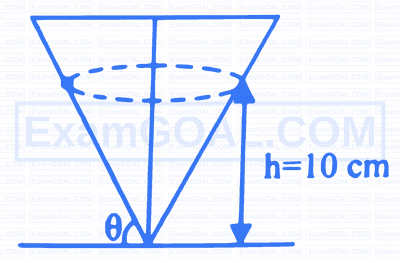
A particle describes a horizontal circle on smooth inner surface of a cone as shown in figure. If the height of the circle above the vertex is 10 cm . The speed of the particle is $\left(\mathrm{g}\right.$, acceleration due to gravity $\left.=10 \mathrm{~m} / \mathrm{s}^2\right)$