Alternating Current · Physics · MHT CET

In an LC circuit, angular frequency at resonance is $\omega$. The new angular frequency when inductance is made four times and capacitance is made eight times is

An inductor of $\left(\frac{100}{\pi}\right) \mathrm{mH}$, capacitor of capacitance $\left(\frac{10^{-3}}{2 \pi}\right) \mathrm{F}$ and resistance of $10 \Omega$ are connected in series with an AC voltage source of $110 \mathrm{~V}, 50 \mathrm{~Hz}$ supply. The tangent of the phase angle ' $\phi$ ' between voltage and current is

$$ \text { The frequency at resonance for the circuit is } $$

In an a.c. circuit containing $L, C, R$ in series the ratio of true power to apparent power is ( $\mathrm{Z}=$ impedance of the circuit and R is the resistance)

In series LCR circuit R $=18 \Omega$ and impedance is $30 \Omega$. An rms voltage 210 V is applied across the circuit. The true power consumed in AC circuit is nearly

A resistor of $5 . \Omega$, inductor of self inductance $\left(\frac{2}{\pi^2}\right) \mathrm{H}$ and a capacitor of unknown capacity are connected in series to an a.c. source of $100 \mathrm{~V}, 50 \mathrm{~Hz}$ supply. When the voltage and current are in phase, the value of capacitance is

$\mathrm{L}, \mathrm{C}$ and R are connected in series to an a. c. source. Which one of the following is true?

Phase relation between current and voltage is such that

In series LCR circuit C $=2 \mu \mathrm{~F}, \mathrm{~L}=5 \mathrm{mH}$ and $\mathrm{R}=5 \Omega$. The ratio of energy stored in the inductor to that in capacitor, when maximum current flows through the circuit is

In an $L R$ circuit, the value of $L$ is $\left(\frac{0.3}{\pi}\right)$ henry and the value of R is $40 \Omega$, If in the circuit, an alternating e.m.f of 230 V at 50 cycles per second is connected, the impedance of the circuit and current will be respectively

In an a.c. circuit, a resistance ' $R$ ' is connected in series with an inductance ' $L$ '. If phase angle between voltage and current is $45^{\circ}$, the value of inductive reactance will be $\left(\tan 45^{\circ}=1\right)$

An a.c. source of frequency ' f ' is connected to a circuit containing an inductance ' $L$ ' and resistance ' R ' in series. The impedance of this circuit is

The reactance of a capacitor is $\mathrm{X}_{\mathrm{C}}$. If the frequency and the capacitance are doubled, then the new reactance will be

An a. c. voltage is applied to pure inductor. The current in the inductor

The power factor of a CR circuit is $\frac{1}{\sqrt{2}}$, If the frequency of a.c. signal is halved, then the power factor of the circuit will become

In LCR series circuit, when ' $L$ ' is removed from the circuit, the phase difference between voltage and current in the circuit is $\frac{\pi}{3}$. If ' $C$ ' is removed from the circuit instead of $L$ then phase difference is again $\frac{\pi}{3}$. The power factor of the circuit is $\left(\tan 60^{\circ}=\sqrt{3}\right)$

If the power factor changes from 0.5 to 0.25 because impedance changes from $Z_1$ to $Z_2$ then $\mathrm{Z}_1=\mathrm{xZ}_2$. The value of x is (Resistance remains constant)

Same current is flowing in two different a.c. circuits. First circuit contains only inductance and second contains only capacitance. If the frequency of a.c. is increased in both circuits, the current will

An a. c. source is connected across a pure inductor. Which one of the following figures shows the correct phase relation between the current and e.m.f.?

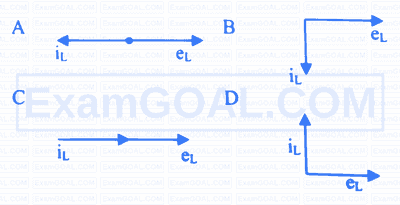
In an a.c. circuit with pure capacitance ' C ' and a.c. source $E=E_0 \sin \omega t$, the equation of instantaneous current is given by

A current of 5 A is flowing at 220 V in a primary coil of a transformer. If the voltage produced in the secondary coil is 2200 V and $50 \%$ of power is lost, then the current in the secondary coil will be

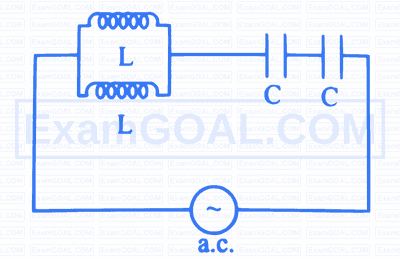
Figure shows the combination of inductances and capacitances. Resonant frequency of the $\mathrm{L}-\mathrm{C}$ circuit is

An alternating e.m.f. is given by $e=e_0 \sin \omega t$. In how much time the e.m.f. will have half its maximum value, if e starts from zero ?

$$ \left(\mathrm{T}=\text { Time Period, } \sin 30^{\circ}=\frac{1}{2}\right) $$

A coil has inductance 2 H . The ratio of its reactance when it is connected first to an a.c. source and then to a d.c. source is

When a capacitor is connected in series LR circuit, the alternating current flowing in the circuit

When alternating current is passed through $\mathrm{L}-\mathrm{R}$ series circuit, the power factor is $\frac{\sqrt{3}}{2}$ and $\mathrm{R}=50 \Omega$, then the value of L is

$$ \left[\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}, \sin \frac{\pi}{6}=\frac{1}{2}, \tan \frac{\pi}{6}=\frac{1}{\sqrt{3}}\right] $$

An a.c. e.m.f. of peak value 230 V and frequency 50 Hz is connected to a circuit with $\mathrm{R}=11.5 \Omega, \mathrm{~L}=2.5 \mathrm{H}$ and a capacitor all in series. The value of capacitance is ' $C$ ' for the current in the circuit to be maximum. The value of ' $C$ ' and maximum current are respectively ( $\pi^2=10$ )

An ideal inductor of $\left(\frac{1}{\pi}\right) \mathrm{H}$ is connected in series with a $300 \Omega$ resistor. If a $20 \mathrm{~V}, 200 \mathrm{~Hz}$ alternating source is connected across the combination, the phase difference between the voltage and current is

An alternating e.m.f. having voltage $\mathrm{V}=\mathrm{V}_0 \sin \omega t$ is applied to a series L-C-R circuit. Given : $\left|X_L-X_C\right|=R$. The r.m.s. value of potential difference across capacitor will be

In an electrical circuit ' $R$ ', ' $L$ ', ' $C$ ' and an a.c. voltage source are all connected in series. When ' L ' is removed from the circuit, the phase difference between the voltage and the current in the circuit is $\frac{\pi}{3}$. If instead ' $C$ ' is removed from the circuit, the phase difference is again $\frac{\pi}{3}$. The power factor of the circuit is $\left(\tan \frac{\pi}{3}=\sqrt{3}\right)$

In series LCR resonant circuit, R $=800 \Omega$, $\mathrm{C}=2 \mu \mathrm{~F}$ and voltage across resistance is 200 V . The angular frequency is $250 \mathrm{rad} / \mathrm{s}$. At resonance, the voltage across the inductance is

If maximum energy is stored in a capacitor at $\mathrm{t}=0$ then the time after which, current in the circuit will be maximum is

In LCR series circuit, R = 18 $\Omega$ and impedance $33 \Omega$. An r.m.s. voltage of 220 V is applied across the circuit. The true power consumed in a.c. circuit is

An a.c. e.m.f. of peak value $=230 \mathrm{~V}$ and frequency 50 Hz is connected to a circuit with $\mathrm{R}=11.5 \Omega, \mathrm{~L}=2.5 \mathrm{H}$ and a capacitor all in series. The value of capacitance is ' C ' for the current in the circuit to be maximum. The value of C and maximum current are respectively $\left(\pi^2=10\right)$.

An e.m.f. $e=E_0 \cos \omega t$ is applied to a circuit containing $L, C$ and $R$ in series where $X_L=3 R$ and $\mathrm{X}_{\mathrm{C}}=\mathrm{R}$. The average power dissipated in the circuit is

An ideal transformer converts 220 a.c. to 3.3 kV a.c. to transmit a power of 4.4 kW . If primary coil has 600 turns then alternating current in secondary coil is

A coil of self-inductance $L$ is connected in series with a bulb and an a. c. source. Brightness of the bulb decreases when

A $20 \Omega$ resistance, 10 mH inductance coil and $15 \mu \mathrm{~F}$ capacitor are joined in series. When a suitable frequency alternating current source is joined to this combination, the circuit resonates. If the resistance is made $\frac{1}{3} \mathrm{rd}$, the resonant frequency

A resistance of $200 \Omega$ and an inductor of $\frac{1}{2 \pi} \mathrm{H}$ are connected in series to a.c. voltage of 40 V and 100 Hz frequency. The phase angle between the voltage and current is

A coil of resistance $450 \Omega$ and self-inductance 1.5 henry is connected to an a.c. source of frequency $\frac{150}{\pi} \mathrm{~Hz}$. The phase difference between voltage and current is

In an $L-R$ circuit, the inductive reactance is equal to $\sqrt{3}$ times the resistance ' $R$ ' of the circuit. An e.1n.f. $\mathrm{E}=\mathrm{E}_0 \sin (\omega \mathrm{t})$ is applied to the circuit. The power consumed in the circuit is

An a.c. source is applied to a series LR circuit with $\mathrm{X}_{\mathrm{L}}=3 \mathrm{R}$ and power factor is $\mathrm{X}_1$. Now a capacitor with $\mathrm{X}_{\mathrm{c}}=\mathrm{R}$ is added in series to LR circuit and the power factor is $\mathrm{X}_2$. The ratio $\mathrm{X}_1$ to $\mathrm{X}_2$ is

An inductance of 2 mH , a condenser of $20 \mu \mathrm{~F}$ and a resistance of $50 \Omega$ are connected in series to an a.c. source. The reactance of inductor and condenser are same. The reactance of either of them will be

In an $L C R$ circuit, if ' $V$ ' is the effective value of the applied voltage, $V_R$ is the voltage across ' $R$ ', ' $\mathrm{V}_{\mathrm{L}}$ ' and ' $\mathrm{V}_{\mathrm{C}}$ ' is the effective voltage across ' L ' and ' $C$ ' respectively then

A light bulb connected in series with a capacitor and an a.c. source is glowing with a certain brightness. On reducing the capacity of capacitance and frequency of source, the brightness of the lamp (respectively)

If a transformer of an audio amplifier has output impedance $8000 \Omega$ and the speaker has input impedance $8 \Omega$, the primary and secondary turns of this transformer connected between the output of amplifier and to loudspeaker should have the ratio

In LCR series circuit, an alternating e.m.f. 'e' and current ' $i$ ' are given by equations $\mathrm{e}=160 \sin (100 \mathrm{t})$ Volt and $\mathrm{i}=250 \sin \left(100 \mathrm{t}+\frac{\pi}{3}\right) \mathrm{mA}$. The average power dissipated in the circuit is

An electric lamp connected in series with a capacitor and an a.c. source is glowing with certain brightness. On increasing the value of capacitance the brightness of the lamp

The alternating voltage is given by $\mathrm{v}=\mathrm{v}_0 \sin \left(\omega \mathrm{t}+\frac{\pi}{3}\right)$ when will be the voltage maximum for first time?

The core used in transformers are laminated to

A coil has inductance H . The ratio of its reactance when it is connected first to an a.c. source and then to d.c. source is

A resistor of $50 \Omega$, inductor of self inductance $\left(\frac{3}{\pi^2}\right) \mathrm{H}$ and a capacitor of unknown capacity are connected in series to an a.c. source of 100 V and 50 Hz . When the voltage and current are in phase, the value of capacitance is (nearly)

Which one of the following graph represent correctly the variation of impedance $(\mathrm{Z})$ of a series LCR circuit with the frequency $(v)$ of applied a.c.?

When a coil is connected to a d.c. source of e.m.f. 12 volt; then the current of 4 A flows in it . If the same coil is connected to a 12 volt, 50 Hz a.c. source, then the current flowing in it is 2.4 A . Then self-inductance of the coil will be

In an a.c. circuit, the reactance of a coil is $\sqrt{3}$ times its resistance. The phase difference between the voltage across the coil to the current through the coil will be

A series $\mathrm{L}-\mathrm{C}-\mathrm{R}$ circuit containing a resistance ' $R$ ' has angular frequency ' $\omega$ '. At resonance the voltage across resistance and inductor are ' $V_R$ ' and ' $\mathrm{V}_{\mathrm{L}}$ ' respectively, then value of capacitance will be

Alternating current of peak value $\left(\frac{2}{\pi}\right)$ A flows through the primary coil of a transformer. The coefficient of mutual inductance between primary and secondary coils is 1 H . The peak e.m.f. induced in secondary coil (Frequency of a.c. $=50 \mathrm{~Hz}$ )

When 100 V d.c. is applied across a solenoid, a current of 1 A flows in it. When 100 a.c. is applied across it, the current drops to 0.5 A. If the frequency is 50 Hz , the impedance and inductance is

A $1 \mu \mathrm{~F}$ capacitor is charged to 50 V and is then discharged through 10 mH inductor of negligible resistance. The maximum current in the inductor is

In LCR resonant circuit, the current and voltage have phase difference

An inductance of $\frac{300}{\pi} \mathrm{mH}$, a capacitance of $\frac{1}{\pi} \mathrm{mF}$ and a resistance of $20 \Omega$ are connected in series with an a.c. source of $240 \mathrm{~V}, 50 \mathrm{~Hz}$. The phase angle of the circuit is

With an alternating voltage source frequency ' f ', inductor ' $L$ ', capacitor ' $C$ ' and resistance ' $R$ ' are connected in series. The voltage leads the current by $45^{\circ}$. The value of ' $L$ ' is $\left(\tan 45^{\circ}=1\right)$

With gradual increase in frequency of an a.c. supply, the impedance of an LCR series circuit

An a.c. voltage source $\mathrm{V}=\mathrm{V}_0 \sin \omega \mathrm{t}$ is connected across resistance ' $R$ ' and capacitance ' $C$ ' in series. It is given that $R=\frac{1}{\omega c}$ and the peak current is $\mathrm{I}_0$. If the angular frequency of the voltage source is changed to $\left(\frac{\omega}{\sqrt{3}}\right)$, then the new peak current in the circuit is

A transformer has 120 turns in the primary coil and carries 5 A current. Input power is one kilowatt. To have 560 V output, the number of turns in secondary coil will be

In series LCR circuit, 'R' represents resistance of electric bulb. If the frequency of a.c. supply is doubled, the value of inductance ' $L$ ' and capacitance 'C' should be

For the series $L C R$ circuit, $R=\frac{X_L}{2}=2 \mathrm{X}_{\mathrm{c}}$. The impedance of the circuit and the phase difference between V and I will be

An e.m.f. $E=E_0 \cos \omega t$ is applied to the $L-R$ circuit. The inductive reactance is equal to the resistance ' $R$ ' of the circuit. The power consumed in the circuit is

A series resonant circuit consists of inductor ' $L$ ' of negligible resistance and a capacitor ' $C$ ' which produces resonant frequency ' $f$ '. If $L$ is changed to 3 L and ' C ' is changed to 6 C , the resonant frequency will become.

The inductive reactance of a coil is ' $R$ ' $\Omega$. If inductance of a coil is tripled and frequency of a.c supply is also tripled, then new inductive reactance will be

An e.m.f. $E=E_0 \cos \omega t$ is applied to circuit containing L and R in series. If $\mathrm{X}_{\mathrm{L}}=2 \mathrm{R}$, then the power dissipated in the circuit is

When a capacitor is connected in series LR circuit, the alternating current flowing in the circuit

Average power associated with an ideal inductor and ideal capacitor over a complete cycle of a.c. is respectively

LC series resonant circuit produces resonant frequency ' $f$ '. If ' $L$ ' is tripled and ' $C$ ' is increased by $3 C$, the resonant frequency will be

When a capacitor is connected in series LR circuit, the alternating current flowing in the circuit

An alternating current is given by $\mathrm{I}=100 \sin (50 \pi \mathrm{t})$. How many times will the current become zero in one second?

A coil of self inductance L is connected in series with a bulb B and an a.c. source. Brightness of the bulb decreases when

In series LCR resonant circuit, the capacitance is changed from C to 3 C . To obtain the same resonant frequency, the inductance should be changed from $L$ to

For the given figure, choose the correct option.

In LCR series circuit if the frequency is increased, the impedance of the circuit

An inductor of inductance $2 \mu \mathrm{H}$ is connected in series with a resistance, a variable capacitor and an a.c. source of frequency 5 kHz . The value of capacitance for which maximum current is drawn into the circuit is $\frac{1}{\mathrm{x}} \mathrm{F}$, where the value of ' $x$ ' is (Take $\pi^2=10$)

When 80 volt d.c. is applied across a solenoid, a current of 0.8 A flows in it. When 80 volt a.c. is applied across the same solenoid, the current becomes 0.4 A . If the frequency of a.c. source is 50 Hz , the impedance and inductance of the solenoid is nearly

A transformer is used to set up an alternating e.m.f. of 220 V to 4.4 kV to transmit 6.6 kW of power. The primary coil has 1000 turns. The current rating of the secondary coil is (Transformer is ideal)

A series LCR circuit containing a resistance ' R ' has angular frequency ' $\omega$ '. At resonance the voltage across resistance and inductor are ' $\mathrm{V}_{\mathrm{R}}$ ' and ' $V_L$ ' respectively, then value of inductance ' $L$ ' will be

A 42 mH inductor is connected to $200 \mathrm{~V}, 50 \mathrm{~Hz}$ a.c. supply. The r.m.s. value of current in the circuit will be nearly [ Take $\pi=\frac{22}{7}$ ]

An alternating voltage $\mathrm{v}=200 \sqrt{2} \sin (100 \mathrm{t})$ is connected to a $1 \mu \mathrm{~F}$ capacitor through an a. c. ammeter. The reading of the ammeter shall be

Three inductances are connected as shown in figure. The equivalent inductance is

In an $A C$ circuit $E=200 \sin (50 t)$ volt and $\mathrm{I}=100 \sin \left(50 \mathrm{t}+\frac{\pi}{3}\right) \mathrm{mA}$. The power dissipated in the circuit is

$$\binom{\sin 30^{\circ}=\cos 60^{\circ}=0.5}{\sin 60^{\circ}=\cos 30^{\circ}=\sqrt{3} / 2}$$

A transformer having efficiency $90 \%$ is working on 200 V and 3 kw power supply. If the current in the secondary coil is 6 A , the voltage across the secondary coil and the current in the primary coil are respectively

An inductance coil has a resistance of $80 \Omega$. When on AC signal of frequency 480 Hz is applied to the coil, the voltage leads the current by $45^{\circ}$. The inductance of the coil in henry is $\left[\sin 45^{\circ}=\cos 45^{\circ}=1 / \sqrt{2}\right]$

$\mathrm{L}=2 \mathrm{H}, \mathrm{C}=5 \mathrm{mF}$ and $\mathrm{R}=12 \Omega$ are connected in series to an a.c. generator of frequency 50 Hz . Then

The magnetic energy in an inductor changes from maximum value to minimum value in 5 ms . When connected to an a.c. source, the frequency of the source is

The core used in transformer and other electromagnetic devices is laminated to

In an a.c. circuit $\mathrm{I}=100 \sin 200 \pi \mathrm{t}$. The time required for the current to achieve its peak value will be

In an A.C. circuit, the potential difference ' $V$ ' and current 'I' are given respectively by $\mathrm{V}=100 \sin (100 \mathrm{t}) \mathrm{V}, \mathrm{I}=100 \sin \left(100 \mathrm{t}+\frac{\pi}{3}\right) \mathrm{mA}$ The power dissipated in the circuit will be [Given $\rightarrow \cos \frac{\pi}{3}=\frac{1}{2}$]

In the given circuit, when $S_1$ is closed, the capacitor gets fully charged. Now $\mathrm{S}_1$ is open and $\mathrm{S}_2$ is closed. Then

The power factor of an R-L circuit is $$\frac{1}{\sqrt{2}}$$. If the frequency of $$\mathrm{AC}$$ is doubled the power factor will now be

An alternating voltage $$E=200 \sqrt{2} \sin (100 t)$$ volt is connected to a $$1 \mu \mathrm{f}$$ capacitor through an a.c. ammeter. The reading of the ammeter shall

What will be the phase difference between virtual voltage and virtual current when current in the circuit is wattless?

A coil having an inductance of $$\frac{1}{\pi} \mathrm{H}$$ is connected in series with a resistance of $$300 \Omega$$. If $$20 \mathrm{~V}$$ from a $$200 \mathrm{~Hz}$$ source are impressed across the combination, the value of the phase angle between the voltage and the current is

An alternating voltage is applied to a series LCR circuit. If the current leads the voltage by $$45^{\circ}$$, then $$\left(\tan 45^{\circ}=1\right)$$

For a purely inductive or a purely capacitive circuit, the power factor is

The reciprocal of the total effective resistance of LCR a.c. circuit is called

The number of turns in the primary and the secondary of a transformer are 1000 and 3000 , respectively. If $$80 \mathrm{~V} \mathrm{~AC}$$ is applied to the primary coil of the transformer, then the potential difference per turn of the secondary coil would be

A group of lamps having total power rating of $$1000 \mathrm{~W}$$ is supplied by an AC voltage of $$E=200 \sin \left(310 t+60^{\circ}\right)$$, the rms value of current flowing through the circuit is

At a particular angular frequency, the reactance of capacitor and that of inductor is same. If the angular frequency is doubled, the ratio of the reactance of the capacitor to that of the inductor will be

In a $$L$$-$$R$$ circuit the inductive reactance is equal to the resistance $R$ in the circuit. An emf $$E=E_0 \cos \omega t$$ is applied to the circuit. The power consumed in the circuit is

In an oscillating LC circuit, the maximum charge on the capacitor is '$$Q$$'. When the energy is stored equally between the electric and magnetic fields, the charge on the capacitor becomes

With increase in frequency of a.c. supply, the impedance of an L-C-R series circuit

In an a.c. circuit the instantaneous current and emf are represented as $$\mathrm{I}=\mathrm{I}_0, \sin [\omega \mathrm{t}-\pi / 6]$$ and $$\mathrm{E}=\mathrm{E}_0 \sin [\omega \mathrm{t}+\pi / 3]$$ respectively. The voltage leads the current by

When an inductor '$$L$$' and a resistor '$$R$$' in series are connected across a $$15 \mathrm{~V}, 50 \mathrm{~Hz}$$ a.c. supply, a current of $$0.3 \mathrm{~A}$$ flows in the circuit. The current differs in phase from applied voltage by $$\left(\frac{\pi}{3}\right)^c$$. The value of '$$R$$' is $$\left(\sin \frac{\pi}{6}=\cos \frac{\pi}{3}=\frac{1}{2}, \sin \frac{\pi}{3}=\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}\right)$$

An a.c. source of $$15 \mathrm{~V}, 50 \mathrm{~Hz}$$ is connected across an inductor (L) and resistance (R) in series R.M.S. current of $$0.5 \mathrm{~A}$$ flows in the circuit. The phase difference between applied voltage and current is $$\left(\frac{\pi}{3}\right)$$ radian. The value of resistance $$(\mathrm{R})$$ is $$\left(\tan 60^{\circ}=\sqrt{3}\right)$$

Resistor of $$2\Omega$$, inductor of $$100 \mu \mathrm{H}$$ and capacitor of $$400 \mathrm{pF}$$ are connected in series across a source of $$\mathrm{e}_{\mathrm{rms}}=0.1$$ Volt. At resonance, voltage drop across inductor is

In the given circuit, r.m.s. value of current through the resistor $$\mathrm{R}$$ is

In the given circuit, if $$\frac{\mathrm{dI}}{\mathrm{dt}}=-1 \mathrm{~A} / \mathrm{s}$$ then the value of $$\left(V_A-V_B\right)$$ at this instance will be

An inductor of $$0.5 \mathrm{~mH}$$, a capacitor of $$20 ~\mu \mathrm{F}$$ and a resistance of $$20 \Omega$$ are connected in series with a $$220 \mathrm{~V}$$ a.c. source. If the current is in phase with the e.m.f. the maximum current in the circuit is $$\sqrt{x} A$$. The value of '$$x$$' is

The a.c. source is connected to series LCR circuit. If voltage across $$R$$ is $$40 \mathrm{~V}$$, that across $$\mathrm{L}$$ is $$80 \mathrm{~V}$$ and that across $$\mathrm{C}$$ is $$40 \mathrm{~V}$$, then the e.m.f. '$$e$$' of a.c. source is

In a series LCR circuit, $$\mathrm{C}=2 \mu \mathrm{F}, \mathrm{L}=1 \mathrm{mH}$$ and $$\mathrm{R}=10 \Omega$$. The ratio of the energies stored in the inductor and the capacitor, when the maximum current flows in the circuit, is

The a.c. source of e.m.f. with instantaneous value '$$e$$' is given by $$e=200 \sin (50 t)$$ volt. The r.m.s. value of current in a circuit of resistance $$50 \Omega$$ is

With the gradual increase in frequency of an a. c. source, the impedance of an LCR series circuit

In series LCR circuit, the voltage across the inductance and the capacitance are not

With an alternating voltage source of frequency '$$f$$', inductor '$$L$$', capacitor '$$C$$' and resistance '$$R$$' are connected in series. The voltage leads the current by $$45^{\circ}$$. The value of '$$L$$' is $$\left(\tan 45^{\circ}=1\right)$$

The capacitive reactance of a capacitor '$$C$$' is $$\mathrm{X} \Omega$$. Both, the frequency of a.c. supply and capacitance of the above capacitor are doubled. The new capacitive reactance will be

A $$100 \mathrm{~mH}$$ coil carries a current of $$1 \mathrm{~A}$$. Energy stored in the form of magnetic field is

In the circuit given below, the current through inductor is $$0.9 \mathrm{~A}$$ and through the capacitor is $$0.6 \mathrm{~A}$$. The current drawn from the a.c. source is

The inductive reactance of a coil is '$$\mathrm{X}_{\mathrm{L}}$$'. If the inductance of a coil is tripled and frequency of a.c. supply is doubled, then the new inductive reactance will be

In the circuit shown the ratio of quality factor and the bandwidth is

In a series LR circuit, $$X_L=R$$, power factor is $$P_1$$. If a capacitor of capacitance $$C$$ with $$X_C=X_L$$ is added to the circuit the power factor becomes $$P_2$$. The ratio of $$P_1$$ to $$P_2$$ will be

An e.m.f. $$E=4 \cos (1000 t)$$ volt is applied to an LR circuit of inductance $$3 \mathrm{~mH}$$ and resistance $$4 ~\Omega$$. The maximum current in the circuit is

An alternating voltage of frequency '$$\omega$$' is induced in electric circuit consisting of an inductance '$$L$$' and capacitance '$$C$$', connected in parallel. Then across the inductance coil

The reactance of capacitor at $$50 \mathrm{~Hz}$$ is $$5 \Omega$$. If the frequency is increased to $$100 \mathrm{~Hz}$$, the new reactance is

The coil of an a.c. generator has 100 turns, each of cross-sectional area $$2 \mathrm{~m}^2$$. It is rotating at constant angular speed $$30 ~\mathrm{rad} / \mathrm{s}$$, in a uniform magnetic field of $$2 \times 10^{-2} \mathrm{~T}$$. If the total resistance of the circuit is $$600 ~\Omega$$ then maximum power dissipated in the circuit is

A capacitor, an inductor and an electric bulb are connected in series to an a.c. supply of variable frequency. As the frequency of the supply is increased gradually, then the electric bulb is found to

In an $$\mathrm{AC}$$ circuit, the current is $$\mathrm{i}=5 \sin \left(100 \mathrm{t}-\frac{\pi}{2}\right) \mathrm{A}$$ and voltage is $$\mathrm{e}=200 \sin (100 \mathrm{t})$$ volt. Power consumption in the circuit is $$\left(\cos 90^{\circ}=0\right)$$

A capacitor of capacitance $$50 \mu \mathrm{F}$$ is connected to a.c. source $$\mathrm{e}=220 \sin 50 \mathrm{t}$$ ($$\mathrm{e}$$ in volt, $$\mathrm{t}$$ in second). The value of peak current is

The resistance offered by an inductor $$\left(X_L\right)$$ in an a.c. circuit is

A coil having an inductance of $$\frac{1}{\pi} \mathrm{H}$$ is connected in series with a resistance of $$300 \Omega$$. If A.C. Source $$(20 \mathrm{~V}-200 \mathrm{~Hz})$$ is connected across the combination, the phase angle between voltage and current is

In a full wave rectifier circuit without filter, the output current is

A rejector circuit is the resonant circuit in which

In series LCR circuit, at resonance the peak value of current will be [$$\mathrm{E_0}$$ is peak emf, R is resistance, $$\omega \mathrm{L}$$ is inductive reactance and $$\omega \mathrm{C}$$ is capacitive]

An alternating e.m.f. is $$\mathrm{e}=\mathrm{e}_0 \sin \omega \mathrm{t}$$. In what time the e.m.f. will have half its maximum value, if '$$\mathrm{e}$$' starts from zero? ($$\mathrm{T}=$$ time period, $$\sin 30^{\circ}=0.5$$)

A step up transformer operates on $$220 \mathrm{~V}$$ and supplies current of $$2 \mathrm{~A}$$. The ratio of primary and secondary windings is $$1: 20$$. The current in the primary is

In the part of an a.c. circuit as shown, the resistance $$R=0.2 \Omega$$. At a certain instant $$(\mathrm{V_A-V_B})= 0.5 \mathrm{~V}, \mathrm{I}=0.5 \mathrm{~A}$$ and $$\frac{\Delta \mathrm{I}}{\Delta \mathrm{t}}=8 \mathrm{~A} / \mathrm{s}$$. The inductance of the coil is

In the circuit shown in the figure, a.c. source gives voltage $$\mathrm{V}=20 \cos (2000 \mathrm{t})$$. Impedance and r.m.s. current respectively will be

Which graph shows the correct variation of r.m.s. current 'I' with frequency 'f' of a.c. in case of (LCR) parallel resonance circuit?

The peak value of an alternating emf '$$\mathrm{e}$$' given by $$\mathrm{e}=\mathrm{e}_0 \cos \omega \mathrm{t}$$ is 10 volt and its frequency is $$50 \mathrm{~Hz}$$. At time $$\mathrm{t}=\frac{1}{600} \mathrm{~s}$$, the instantaneous e.m.f is $$\left(\cos \frac{\pi}{6}=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}\right)$$

A circuit containing resistance R$$_1$$, inductance L$$_1$$ and capacitance C$$_1$$ connected in series resonates at the same frequency 'f$$_0$$' as another circuit containing R$$_2$$, L$$_2$$ and C$$_2$$ in series. If two circuits are connected in series then the new frequency at resonance is

A series L-C-R circuit containing a resistance of $$120 ~\Omega$$ has angular frequency $$4 \times 10^5 \mathrm{~rad} \mathrm{~s}^{-1}$$. At resonance the voltage across resistance and inductor are $$60 \mathrm{~V}$$ and $$40 \mathrm{~V}$$ respectively, then the value of inductance will be

For series LCR circuit, which one of the following is a CORRECT statement?

In an LCR series a.c. circuit, the voltage across each of the components L, C and R is 60 V. The voltage across the LC combination is

If we increase the frequency of an a.c. supply, then inductive reactance

A capacitor of capacity '$$C$$' is charged to a potential '$$V$$'. It is connected in parallel to an inductor of inductance '$$\mathrm{L}$$'. The maximum current that will flow in the circuit is

A step down transformer is used to reduce the main supply from '$$V_1$$' volt to '$$V_2$$' volt. The primary coil draws a current '$$\mathrm{I}_1$$' $$\mathrm{A}$$ and the secondary coil draws '$$\mathrm{I}_2$$' A. $$(\mathrm{I}_1<\mathrm{I}_2)$$. The ratio of input power to output power is

For the circuit shown below, instantaneous current through inductor '$$\mathrm{L}$$' and capacitor '$$\mathrm{C}$$' is respectively.

A parallel plate capacitor having plates of radius 6 cm has capacitance 100 pF. It is connected to 230 V a.c. supply with angular frequency 300 rad/s. The r.m.s. value of current is

A step down transformer has turns ratio $$20: 1$$. If $$8 \mathrm{~V}$$ is applied across $$0.4 \mathrm{~ohm}$$ secondary then the primary current will be

An a.c. source of angular frequency '$$\omega$$' is fed across a resistor '$$R$$' and a capacitor '$$C$$' in series. The current registered is I. If now the frequency of source is changed to $$\frac{\omega}{3}$$ (but maintaining the same voltage), the current in the circuit is found to be halved. The ratio of reactance to resistance at the original frequency '$$\omega$$' will be

In an a.c. circuit, a resistance R = 40 $$\Omega$$ and an inductance 'L' are connected in series. If the phase angle between voltage and current is 45$$^\circ$$, then the value of the inductive reactance is (tan 45$$^\circ$$ = 1)

The frequency of the output signal of an LC oscillator circuit is '$$\mathrm{F}$$' Hz with a capacitance of 0.1 $$\mu \mathrm{F}$$. If the value of the capacitor is increased to $$0.2~ \mu \mathrm{F}$$, then the frequency of the output signal will be

In LCR series resonant circuit, at resonance, voltage across 'L' and 'C' will cancel each other because they are

The inductive reactance of a coil is R$$\Omega$$. If the inductance of a coil is doubled and frequency of a.c. supply is also doubled then the new inductive reactance will be

Three pure inductors each of inductance 6H are connected as shown in the figure. Their equivalent inductance between the points 'P' and 'Q' is

The instantaneous value of an alternating current is given by $$\mathrm{i}=50 \sin (100 \pi \mathrm{t})$$. It will achieve a value of $$25 \mathrm{~A}$$ after a time interval of $$\left(\sin 30^{\circ}=0.5\right)$$

In a step up transformer, which one of the following statements is correct?

In the graphical representation of e.m.f. '$$\mathrm{e}$$' and current '$$\mathrm{i}$$' versus '$$\omega \mathrm{t}$$' for an a.c. circuit, both emf and current reach zero, minimum and maximum value at the same time. The circuit element connected to the source will be

An alternating voltge is represented by $$\mathrm{V}=80 \sin (100 \pi \mathrm{t}) \cos (100 \pi \mathrm{t})$$ volt. The peak voltage is

A series combination of resistor 'R' and capacitor 'C' is connected to an a.c. source of angular frequency '$$\omega$$'. Keeping the voltage same, if the frequency is changed to $$\frac{\omega}{3}$$ the current becomes half of the original current. Then the ratio of capacitive reactance and resistance at the former frequency is

An inductive coil has a resistance of $$100 ~\Omega$$. When an a.c. signal of frequency $$1000 \mathrm{~Hz}$$ is applied to the coil the voltage leads the current by $$45^{\circ}$$. The inductance of the coil is $$\left(\tan 45^{\circ}=1\right.$$)

In an ideal step down transformer, out of the following quantities, which quantity increases in the secondary coil?

A series LCR circuit with resistance (R) $$500 ~\mathrm{ohm}$$ is connected to an a.c. source of $$250 \mathrm{~V}$$. When only the capacitance is removed, the current lags behind the voltage by $$60^{\circ}$$. When only the inductance is removed, the current leads the voltage by $$60^{\circ}$$. The impedance of the circuit is $$\left(\tan \frac{\pi}{3}=\sqrt{3}\right)$$

When a d.c. voltage of $$200 \mathrm{~V}$$ is applied to a coil of self-inductance $$\left(\frac{2 \sqrt{3}}{\pi}\right) \mathrm{H}$$, a current of $$1 \mathrm{~A}$$ flows through it. But by replacing d.c. source with a.c. source of $$200 \mathrm{~V}$$, the current in the coil is reduced to $$0.5 \mathrm{~A}$$. Then the frequency of a.c. supply is

An inductor coil wound uniformly has self inductance 'L' and resistance 'R'. The coil is broken into two identical parts. The two parts are then connected in parallel across a battery of 'E' volt of negligible internal resistance. The current through battery at steady state is

An inductor coil takes current 8A when connected to an 100 V and 50 Hz a.c. source. A pure resistor under the same condition takes current of 10A. If inductor coil and resistor are connected in series to an 100V and 40 Hz a.c. supply, then the current in the series combination of above resistor and inductor is

An AC circuit contains resistance of $12 \Omega$ and inductive reactance $5 \Omega$. The phase angle between current and potential difference will be

A step-up transformer has 300 turns of primary winding and 450 turns of secondary winding. A primary is connected to 150 V and the current flowing through it is 9A. The current and voltage in the secondary are

An alternating emf of $$0.2 \mathrm{~V}$$ is applied across an L-C-R series circuit having $$R=4 \Omega, C=80 \mu \mathrm{F}$$ and $$L=200 \mathrm{~mH}$$. At resonance the voltage drop across the inductor is

A 220 V input is supplied to a transformer. The output circuit draws a current of 2.0 A at 440 V . If the ratio of output to input power is 0.8 , then the current drawn by primary winding is

A coil has inductance 2 H . The ratio of its reactance, when it is connected first to an $A C$ source and then to DC source, is

An alternating voltage is given by $E=100 \sin \left(\omega+\frac{\pi}{6}\right) \mathrm{V}$. The voltage will be maximum for the first time when is [ $T=$ periodic time)

In a series $L C R$ circuit $R=300 \Omega, L=0.9 \mathrm{H}$, $C=2 \mu \mathrm{~F}, \omega=1000 \mathrm{rad} / \mathrm{s}$. The impedance of the circuit is