Circular Motion · Physics · MHT CET

A point mass ' $m$ ' attached at one end of a massless, inextensible string of length ' $l$ ' performs a vertical circular motion and the string rotates in vertical plane, as shown in the diagram. The increase in the centripetal acceleration of the point mass when it moves from point A to point C is

[ $\mathrm{g}=$ acceleration due to gravity.]

An inextensible string of length ' $l$ ' fixed at one end, carries a mass ' $m$ ' at the other end. If the string makes $\frac{1}{\pi}$ revolutions per second around the vertical axis through the fixed end, the tension in the string is [The string makes an angle $\theta$ with the vertical]

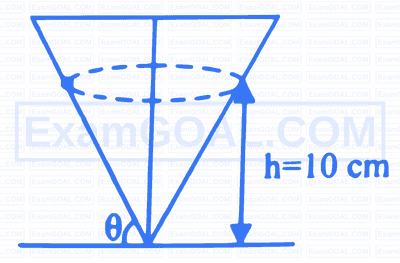
A particle describes a horizontal circle on smooth inner surface of a cone as shown in figure. If the height of the circle above the vertex is 10 cm . The speed of the particle is $\left(\mathrm{g}\right.$, acceleration due to gravity $\left.=10 \mathrm{~m} / \mathrm{s}^2\right)$

Two stones of masses m and 3 m are whirled in horizontal circles, the heavier one in a radius $\left(\frac{\mathrm{r}}{3}\right)$ and lighter one in a radius r . The tangential speed of lighter stone is ' $n$ ' times the value of heavier stone. When the magnitude of centripetal force becomes equal the value of $n$ is

A motor cyclist has to rotate in horizontal circles inside the cylindrical wall of inner radius ' $R$ ' metre. If the coefficient of friction between the wall and the tyres is ' $\mu_{\mathrm{s}}$ ', then the minimum speed required is ( $\mathrm{g}=$ acceleration due to gravity)

The figure shows two masses ' $m$ ' and ' $M$ ' connected by a light string that passes through ${ }_a$ small hole ' $O$ ' at the centre of the table. Mass ' $m$ ' is moved round in a horizontal circle with ' $O$ ' as the centre. The frequency with which ' $m$ ' should be revolved so that ' $M$ ' remains stationary is

( $\mathrm{g}=$ gravitational acceleration)

Radius of curved road is ' $R$ ', width of road is ' $b$ '. The outer edge of road is raised by ' $h$ ' with respect to inner edge so that a car with velocity ' $V$ ' can pass safe over it, then value of ' $h$ ' is ( $\mathrm{g}=$ acceleration due to gravity)

Two bodies of mass 10 kg and 5 kg are moving in concentric circular orbits of radii ' R ' and ' r ' respectively such that their periods are same. The ratio between their centripetal acceleration is

A car is driven on the banked road of radius of curvature 20 m with maximum safe speed. In order to increase its safety speed by $20 \%$, without changing the angle of banking, the increase in the radius of curvature will be [Assume friction is same on the road]

A vehicle is moving with uniform speed along 3 different shaped roads as horizontal, concave and convex. The surface of road on which, the normal reaction on vehicle is maximum is

A body of mass 100 gram is tied to a spring of spring constant $8 \mathrm{~N} / \mathrm{m}$, while the other end of a spring is fixed. If the body moves in a circular path on smooth horizontal surface with constant angular speed $8 \mathrm{rad} / \mathrm{s}$ then the ratio of extension in the spring to its natured length will be

A simple pendulum oscillates with an angular amplitude $\theta$. If the maximum tension in the string is 4 times the minimum tension then the value of $\theta$ is

A pendulum bob has a speed $4 \mathrm{~m} / \mathrm{s}$ at its lowest position. The pendulum is 1 m long. When the length of the string makes an angle of $60^{\circ}$ with the vertical, the speed of the bob at that position is (acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$, $\cos 60^{\circ}=0.5$ )

For a particle moving in a circle with constant angular speed, which of the following statements is 'false'?

A particle performing uniform circular motion of radius $\frac{\pi}{2} \mathrm{~m}$ makes $x$ revolutions in time $t$. Its tangential velocity is

A weightless thread can bear tension up to 3.7 kg wt. A stone of mass 500 gram is tied to it and revolved in circular path of radius 4 m in vertical plane. Maximum angular velocity of the stone will be (acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

The linear speed of a particle at the equator of the earth due to its spin motion is ' V '. The linear speed of the particle at latitude $30^{\circ}$ is

$$\left[\begin{array}{l} \sin 30^{\circ}=\cos 60^{\circ}=1 / 2 \\ \cos 30^{\circ}=\sin 60^{\circ}=\sqrt{3} / 2 \end{array}\right]$$

Two objects of masses ' $m_1$ ' and ' $m_2$ ' are moving in the circles of radii ' $r_1$ ' and ' $r_2$ ' respectively. Their respective angular speeds ' $\omega_1$ ' and ' $\omega_2$ ' are such that they both complete one revolution in the same time ' $t$ '. The ratio of linear speed of ' $m_2$ ' to that of ' $m_1$ ' is

A body performing uniform circular motion of radius ' $R$ ' has frequency ' $n$ '. Its centripetal acceleration per unit radius is proportional to $(n)^x$. The value of $x$ is

A particle starting from rest moves along the circumference of a circle of radius ' $r$ ' with angular acceleration ' $\alpha$ '. The magnitude of the average velocity in time it completes the small angular displacement ' $\theta$ ' is

A particle is moving in a circle with uniform speed. It has constant

A particle of mass ' $m$ ' is performing uniform circular motion along a circular path of radius ' $r$ '. Its angular momentum about the axis passing through the centre and perpendicular to the plane is ' $L$ '. The kinetic energy of the particle is

A particle of mass ' $m$ ' performs uniform circular motion of radius ' $r$ ' with linear speed ' $v$ ' under the application of force ' $F$ '. If ' $m$ ', ' $v$ ' and $' \mathrm{r}$ ' are all increased by $20 \%$ the necessary change in force required to maintain the particle in uniform circular motion, is

A particle rotates in a horizontal circle of radius 'R' in a conical funnel with constant speed 'V'. The inner surface of the funnel is smooth. The height of the plane of the circle from the vertex of the funnel is (g-acceleration due to gravity)

For a particle in uniform circular motion

A disc at rest is subjected to a uniform angular acceleration about its axis. Let $\theta$ and $\theta_1$ be the angle made by the disc in $2^{\text {nd }}$ and $3^{\text {rd }}$ second of its motion. The ratio $\frac{\theta}{\theta_1}$ is

A body moves along a circular path of radius 15 cm . It starts from a point on the circular path and reaches the end of diameter in 3 second, The angular speed of the body in $\mathrm{rad} / \mathrm{s}$ is

A wheel of radius 1 m rolls through $180^{\circ}$ over a plane surface. The magnitude of the displacement of the point of the wheel initially in contact with the surface is.

The string of pendulum of length ' $L$ ' is displaced through $90^{\circ}$ from the vertical and released. Then the maximum strength of the string in order to withstand the tension, as the pendulum passes through the mean position is ( $\mathrm{m}=$ mass of pendulum, $\mathrm{g}=$ acceleration due to gravity)

A particle at rest starts moving with a constant angular acceleration of $4 \mathrm{~rad} / \mathrm{s}^2$ in a circular path. The time at which magnitudes of its centripetal acceleration and tangential acceleration will be equal, is (in second)

A particle is performing uniform circular motion along the circumference of the circle of diameter 1 m with frequency 4 Hz . The acceleration of the particle in $\mathrm{m} / \mathrm{s}^2$ is

A particle moves around a circular path of radius '$$r$$' with uniform speed '$$V$$'. After moving half the circle, the average acceleration of the particle is

On dry road, the maximum speed of a vehicle along a circular path is '$$V$$'. When the road becomes wet, maximum speed becomes $$\frac{\mathrm{V}}{2}$$. If coefficient of friction of dry road is '$$\mu$$' then that of wet road is

A string of length '$$L$$' fixed at one end carries a body of mass '$$\mathrm{m}$$' at the other end. The mass is revolved in a circle in the horizontal plane about a vertical axis passing through the fixed end of the string. The string makes angle '$$\theta$$' with the vertical. The angular frequency of the body is '$$\omega$$'. The tension in the string is

A stone is projected at angle $$\theta$$ with velocity $$u$$. If it executes nearly a circular motion at its maximum point for short time, then the radius of the circular path will be ( $$g=$$ acceleration due to gravity)

A particle is moving in a circle with uniform speed '$$v$$'. In moving from a point to another diametrically opposite point

A body of mass '$$\mathrm{m}$$' attached at the end of a string is just completing the loop in a vertical circle. The apparent weight of the body at the lowest point in its path is ( $$\mathrm{g}$$ = gravitational acceleration)

A railway track is banked for a speed ',$$v$$' by elevating outer rail by a height '$$h$$' above the inner rail. The distance between two rails is 'd' then the radius of curvature of track is ( $$\mathrm{g}=$$ gravitational acceleration)

Two particles having mass '$$M$$' and '$$m$$' are moving in a circular path with radius '$$R$$' and '$$r$$' respectively. The time period for both the particles is same. The ratio of angular velocity of the first particle to the second particle will be

In a conical pendulum the bob of mass '$$\mathrm{m}$$' moves in a horizontal circle of radius '$$r$$' with uniform speed '$$\mathrm{V}$$'. The string of length '$$\mathrm{L}$$' describes a cone of semi vertical angle '$$\theta$$'. The centripetal force acting on the bob is ( $$\mathrm{g}=$$ acceleration due to gravity)

A ball of mass '$$\mathrm{m}$$' is attached to the free end of a string of length '$$l$$'. The ball is moving in horizontal circular path about the vertical axis as shown in the diagram.

The angular velocity '$$\omega$$' of the ball will be [ $$\mathrm{T}=$$ Tension in the string.]

A particle performing uniform circular motion of radius $$\frac{\pi}{2} \mathrm{~m}$$ makes '$$\mathrm{x}$$' revolutions in time '$$t$$'. Its tangential velocity is

A body of mass 200 gram is tied to a spring of spring constant $$12.5 \mathrm{~N} / \mathrm{m}$$, while other end of spring is fixed at point '$$O$$'. If the body moves about '$$O$$' in a circular path on a smooth horizontal surface with constant angular speed $$5 \mathrm{~rad} / \mathrm{s}$$ then the ratio of extension in the spring to its natural length will be

A particle of mass '$$\mathrm{m}$$' moves along a circle of radius '$$r$$' with constant tangential acceleration. If K.E. of the particle is '$$E$$' by the end of third revolution after beginning of the motion, then magnitude of tangential acceleration is

A simple pendulum of length $$2 \mathrm{~m}$$ is given a horizontal push through angular displacement of $$60^{\circ}$$. If the mass of bob is 200 gram, the angular velocity of the bob will be (Take Acceleration due to gravity $$=10 \mathrm{~m} / \mathrm{s}^2$$ ) $$\left(\sin 30^{\circ}=\cos 60^{\circ}=0.5, \cos 30^{\circ}=\sin 60^{\circ}=\sqrt{3} / 2\right)$$

A particle at rest starts moving with constant angular acceleration $$4 ~\mathrm{rad} / \mathrm{s}^2$$ in circular path. At what time the magnitudes of its tangential acceleration and centrifugal acceleration will be equal?

A bucket containing water is revolved in a vertical circle of radius $$r$$. To prevent the water from falling down, the minimum frequency of revolution required is

($$\mathrm{g}=$$ acceleration due to gravity)

A body moving in a circular path with a constant speed has constant

Two bodies of masses '$$\mathrm{m}$$' and '$$3 \mathrm{~m}$$' are rotating in horizontal speed of the body of mass '$$m$$' is $$n$$ times that of the value of heavier body; while the centripetal force is same for both. The value of $$n$$ is

A particle is moving along the circular path with constant speed and centripetal acceleration 'a'. If the speed is doubled, the ratio of its acceleration after and before the change is

A body of mass 'm' is moving with speed 'V' along a circular path of radius 'r'. Now the speed is reduced to $$\frac{V}{2}$$ and radius is increased to '3r'. For this change, initial centripetal force needs to be

A body attached to one end of a string performs motion along a vertical circle. Its centripetal acceleration, when the string is horizontal, will be [$$\mathrm{g}=$$ acceleration due to gravity]

A projectile is thrown with an initial velocity $$(a \hat{i}+b \hat{j}) \mathrm{m} / \mathrm{s}$$, where $$\hat{i}$$ and $$\hat{j}$$ are unit vectors along horizontal and vertical directions respectively. If the range of the projectile is twice the maximum height reached by it, then

A particle is performing U.C.M. along the circumference of a circle of diameter $$50 \mathrm{~cm}$$ with frequency $$2 \mathrm{~Hz}$$. The acceleration of the particle in $$\mathrm{m} / \mathrm{s}^2$$ is

If $$\omega_1$$ is angular velocity of hour hand of clock and $$\omega_2$$ is angular velocity of the earth, then the ratio $$\omega_1$$ : $$\omega_2$$ is

The angular displacement of body performing circular motion is given by $$\theta=5 \sin \frac{\pi t}{6}$$. The angular velocity of the body at $$t=3$$ second will be $$\left[\sin \frac{\pi}{2}=1, \cos \frac{\pi}{2}=0\right]$$

A body performing uniform circular motion of radius 'R' has frequency 'n'. It centripetal acceleration is

The angle of banking '$$\theta$$' for a meter gauge railway line is given by $$\theta=\tan ^{-1}\left(\frac{1}{20}\right)$$. What is the elevation of the outer rail above the inner rail?

A particle moves in a circular orbit of radius '$$r$$' under a central attractive force, $$F=-\frac{k}{r}$$, where $$\mathrm{k}$$ is a constant. The periodic time of its motion is proportional to

A particle at rest starts moving with a constant angular acceleration of $$4 \mathrm{~rad} / \mathrm{s}^2$$ in a circular path. At what time the magnitude of its centripetal acceleration and tangential acceleration will be equal?

A child starts running from rest along a circular track of radius $r$ with constant tangential acceleration a. After time $t$ he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is

[g = acceleration due to gravity]

A body is moving along a circular track of radius 100 m with velocity $20 \mathrm{~m} / \mathrm{s}$. Its tangential acceleration is $3 \mathrm{~m} / \mathrm{s}^2$, then its resultant acceleration will be

A particle starting from rest moves along the circumference of a circle of radius $$r$$ with angular acceleration $$\alpha$$. The magnitude of the average velocity, in the time it completes the small angular displacement $$\theta$$ is

A particle of mass $$m$$ is performing UCM along a circle of radius $$r$$. The relation between centripetal acceleration $$a$$ and kinetic energy $$E$$ is given by

In non-uniform circular motion, the ratio of tangential to radial acceleration is ($$r=$$ radius, $$\alpha=$$ angular acceleration and $$v=$$ linear velocity)

A particle is moving in a radius $$R$$ with constant speed $$v$$. The magnitude of average acceleration after half revolution is

A mass is whirled in a circular path with constant angular velocity and its linear velocity is $v$. If the string is now halved keeping the angular momentum same, the linear velocity is

A body of mass $m$ is performing a UCM in a circle of radius $r$ with speed $v$. The work done by the centripetal force in moving it through $\left(\frac{2}{3}\right) \mathrm{rd}$ of the circular path is

In U.C.M., when time interval $\delta t \rightarrow 0$, the angle between change in velocity ( $\delta \mathbf{v}$ ) and linear velocity $(\boldsymbol{v})$ will be

A particle is performing U.C.M. along the circumference of a circle of diameter 50 cm with frequency 2 Hz . The acceleration of the particle in $\mathrm{m} / \mathrm{s}^2$ is

A stone of mass 1 kg is tied to a string 2 m long and it's rotated at constant speed of $40 \mathrm{~ms}^{-1}$ in a vertical circle. The ratio of the tension at the top and the bottom is [Take $g=10 \mathrm{~ms}^{-2}$]

The real force ' $F$ ' acting on a particle of mass $m$ ' performing circular motion acts along the radius of circle ' $r$ ' and is directed towards the centre of circle. The square root of magnitude of such force is ( $T=$ periodic time)