Simple Harmonic Motion · Physics · MHT CET

All the springs in fig. (a), (b) and (c) are identical, each having force constant K each. Mass m is attached to each system. If $\mathrm{T}_a, \mathrm{~T}_b$ and $\mathrm{T}_{\mathrm{c}}$ are the time periods of oscillations of the three systems in fig. (a), (b) and (c) respectively, then

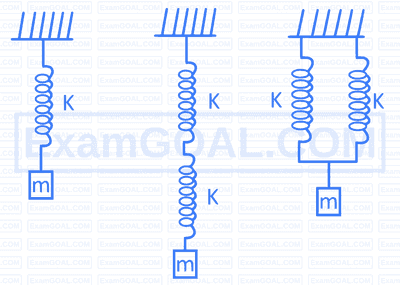
A point particle of mass 200 gram is executing S.H.M. of amplitude 0.2 m . When the particle passes through the mean position, its kinetic energy is $16 \times 10^{-3} \mathrm{~J}$. The equation of motion of this particle is (Initial phase of oscillation $=0^{\circ}$ )

A simple pendulum starts oscillating simple harmonically from its mean position ( $\mathrm{x}=0$ ) with amplitude ' $a$ ' and periodic time ' $T$ '. The magnitude of velocity of pendulum at $x=\frac{a}{2}$ is

A simple pendulum is suspended from ceiling of a lift when lift is at rest its period is ' T '. With what acceleration ' $a$ ' should lift be accelerated upward in order to reduce the period to ' $T$ '? (take ' g ' as acceleration due to gravity)

A particle is performing S.H.M. starting from extreme position. Graphical representation shows that between displacement and acceleration, there is a phase difference of

A mass ' $M$ ' attached to a horizontal spring executes S.H.M. of amplitude $A_1$. When the mass M passes through its mean position, then a smaller mass ' $m$ ' is placed over it and both of them move together with amplitude $\mathrm{A}_2$. The ratio $\left(\frac{A_1}{A_2}\right)$ is

At a place, the length of the oscillating simple pendulum is made $\frac{1}{4}$ times keeping amplitude same then the total energy will be

A spring executes S.H.M. with mass 1 kg attached to it. The force constant of the spring is $4 \mathrm{~N} / \mathrm{m}$. If at any instant its velocity is $20 \mathrm{~cm} / \mathrm{s}$, the displacement at that instant is (Amplitude of S.H.M. is 0.4 m )

The ratio of the frequencies of two simple pendulums is $4: 3$ at the same place. The ratio of their respective lengths is

Two simple pendulums have first (A) bob of mass ' $M_1$ ' and length ' $L_1$ ', second (B) of mass ' $\mathrm{M}_2$ ' and length ' $\mathrm{L}_2$ '. $\mathrm{M}_1=\mathrm{M}_2$ and $\mathrm{L}_1=2 \mathrm{~L}_2$. If their total energies are same then the correct statement is

As shown in the figure, $S_1$ and $S_2$ are identical springs with spring constant K each. The oscillation frequency of the mass ' $m$ ' is ' $f$ '. If the spring $\mathrm{S}_2$ is removed, the oscillation frequency will become

A particle starts oscillating simple harmonically from its mean position with time period ' $T$ '. At time $\mathrm{t}=\frac{\mathrm{T}}{6}$, the ratio of the potential energy to kinetic energy of the particle is

$$ \left[\sin 30^{\circ}=\cos 60^{\circ}=0 \cdot 5, \cos 30^{\circ}=\sin 60^{\circ}=\sqrt{3} / 2\right] $$

Two particles ' $A$ ' and ' $B$ ' execute SHMs of periods ' $T$ ' and $\frac{3 T}{2}$. If they start from the mean position then the phase difference between them, when the particle ' $A$ ' completes two oscillations will be

A small sphere oscillates simple harmonically in a watch glass whose radius of curvature is 1.6 m . The period of oscillation of the sphere is (acceleration due to gravity $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

The displacement of particle in S.H.M. is $\mathrm{x}=\mathrm{A} \cos (\omega \mathrm{t}+\pi / 6)$. Its speed will be maximum at time $\left(\sin 90^{\circ}=1\right)$

An object of mass 0.2 kg executes simple harmonic oscillations along the x -axis with frequency of $\left(\frac{25}{\pi}\right) \mathrm{Hz}$. At the position $x=0.04 \mathrm{~m}$, the object has kinetic energy 1 J and potential energy 0.6 J . The amplitude of oscillation is

The motion of the particle is given by the equation $\mathrm{x}=\mathrm{A} \sin \omega \mathrm{t}+\mathrm{B} \cos \omega \mathrm{t}$.

The motion of the particle is

A particle is executing S.H.M. of amplitude ' $A$ '. When the potential energy of the particle is half of its maximum value during the oscillation, its displacement from the equilibrium position is

A particle is executing linear S.H.M. starting from mean position. The ratio of the kinetic energy to the potential energy of the particle at a point of half the amplitude is

The amplitude of a damped oscillator becomes $\left(\frac{1}{3}\right)^{\mathrm{rd}}$ of original amplitude in 2 seconds. If its amplitude after 6 second become $\left(\frac{1}{n}\right)$ times the original amplitude, the value of $n$ is ( $n$ is non zero integer)

A particle executes S.H.M. starting from the mean position. Its amplitude is ' a ' and its periodic time is ' $T$ '. At a certain instant, its speed ' $u$ ' is half that of maximum speed $\mathrm{V}_{\text {max }}$. The displacement of the particle at that instant is

A particle performing linear S.H.M. has period 8 seconds. At time $\mathrm{t}=0$, it is in the mean position. The ratio of the distances travelled by the particle in the $1^{\text {st }}$ and $2^{\text {nd }}$ second is $\left(\cos 45^{\circ}=1 / \sqrt{2}\right)$

For a particle performing S.H.M.; the total energy is ' $n$ ' times the kinetic energy, when the displacement of a particle from mean position is $\frac{\sqrt{3}}{2} \mathrm{~A}$, where A is the amplitude of S.H.M. The value of ' $n$ ' is

The length of the simple pendulum is made 3 times the original length. If ' T ' is its original time period, then the new time period will be

Two simple harmonic motions of angular frequency $300 \mathrm{rad} / \mathrm{s}$ and $3000 \mathrm{rad} / \mathrm{s}$ have same amplitude. The ratio of their maximum accelerations is

A mass $m$ is suspended from a spring of negligible mass. The spring is pulled a little and then released, so that mass executes S.H.M. of time period $T$. If the mass is increased by $m_0$, the periodic time becomes $\frac{5 \mathrm{~T}}{4}$. The ratio $\frac{\mathrm{m}_0}{\mathrm{M}}$

A simple pendulum has time period ' $\mathrm{T}_1$ '. The point of suspension is now moved upward according to equation $\mathrm{y}=\mathrm{kt}^2$ where $\mathrm{k}=1 \mathrm{~m} / \mathrm{s}^2$. If new time period is ' $\mathrm{T}_2$ ' then $\mathrm{T}_1^2 / \mathrm{T}_2^2$ will be ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

A mass attached to a spring performs S.H.M. whose displacement is $\mathrm{x}=3 \times 10^{-3} \cos 2 \pi \mathrm{t}$ metre. The time taken to obtain maximum speed for the first time is

A mass $x$ gram is suspended from a light spring. It is pulled in downward direction and released so that mass performs S.H.M. of period T. If mass is increased by Y gram, the period becomes $\frac{4 \mathrm{~T}}{3}$. The ratio of $\mathrm{Y} / \mathrm{x}$ is

The period of S. H.M. of a particle is 16 second. The phase difference between the positions at $\mathrm{t}=2 \mathrm{~s}$ and $\mathrm{t}=4 \mathrm{~s}$ will be

If the period of a oscillation of mass ' m ' suspended from a spring is 2 s , then the period of suspended mass ' 4 m ' with the same spring will be

A particle oscillates in straight line simple harmonically with period 8 second and amplitude $4 \sqrt{2} \mathrm{~m}$. Particle starts from mean position. The ratio of the distance travelled by it in $1^{\text {st }}$ second of its motion to that in $2^{\text {nd }}$ second is $\left(\sin 45^{\circ}=1 / \sqrt{2}, \sin \frac{\pi}{2}=1\right)$

A vertical spring oscillates with period 6 second with mass $m$ is suspended from it. When the mass is at rest, the spring is stretched through a distance of (Take, acceleration due to gravity, $\mathrm{g}=\pi^2=10 \mathrm{~m} / \mathrm{s}^2$ )

For a particle performing; S.H.M. the displacement - time graph is shown.

For that particle the force - time graph is correctly shown in graph

If the length of the oscillating simple pendulum is made $\frac{1}{3}$ times the original keeping amplitude same then increase in its total energy at a place will be

' $P$ ' and ' $Q$ ' are fixed points in same plane and mass ' $m$ ' is tied by string as shown in figure. If the mass is displaced slightly out of this plane and released, it will oscillate with time period $(\mathrm{PQ}=2 \mathrm{~d}, \mathrm{PR}=\mathrm{QR}=\mathrm{L})(\mathrm{g}=$ gravitational acceleration)

The bob of a pendulum of length ' $l$ ' is pulled aside from its equilibrium position through an angle ' $\theta$ ' and then released. The bob will then pass through its equilibrium position with speed ' $v$ ', where ' $v$ ' equal to ( $g=$ acceleration due to gravity)

The kinetic energy of a particle, executing simple harmonic motion is 16 J when it is in mean position. If amplitude of motion is 25 cm and the mass of the particle is 5.12 kg , the period of oscillation is

A particle performs linear S.H.M. At a particular instant, velocity of the particle is ' $u$ ' and acceleration is ' $\alpha$ ' while at another instant, velocity is ' $v$ ' and acceleration is ' $\beta$ ' $(0<\alpha<\beta)$. The distance between the two positions is

A particle executing S.H.M. has velocities ' $\mathrm{V}_1$ ' and ' $\mathrm{V}_2$ ' at distances ' $x_1$ ' and ' $x_2$ ' respectively, from the mean position. Its frequency is

For a particle executing S.H.M. having amplitude A, the speed of the article is $\left(\frac{1}{3}\right)^{\text {rd }}$ of its maximum speed when the displacement from the mean position is

The motion of a particle is described by the equation $a=-b x$ where ' $a$ ' is the acceleration, x is the displacement from the equilibrium position and b is a constant. The periodic time will be

A horizontal platform with a small object placed on it executes a linear S.H.M. in the vertical direction. The amplitude of oscillation is 40 cm . What should be the least period of these oscillations, so that the object is not detached from the platform? [Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$]

Starting from mean position, a body oscillates simple harmonically with a period ' $T$ '. After what time will its kinetic energy be $75 \%$ of the total energy? $\left(\sin 30^{\circ}=0.5\right)$

The maximum velocity of a particle, executing S.H.M. with an amplitude 7 mm is $4.4 \mathrm{~ms}^{-1}$ The period of oscillation is $\left[\pi=\frac{22}{7}\right]$

A particle is performing S.H.M. about its mean position with an amplitude ' $a$ ' and periodic time ' $T$ '. The speed of the particle when its displacement from mean position is $\frac{a}{3}$ will be

A piece of wood has length, breadth and height, ' $a$ ', ' $b$ ' and ' $c$ ' respectively. Its relative density, is ' $d$ '. It is floating in water such that the side ' $a$ ' is vertical. It is pushed down a little and released. The time period of S.H.M. executed by it is ($\mathrm{g}=$ acceleration due to gravity)

All the springs in fig. (a), (b) and (c) are identical, each having force constant K . Mass attached to each system is ' $m$ '. If $T_a, T_b$ and $T_c$ are the time periods of oscillations of the three systems respectively, then

A simple pendulum of length ' $L$ ' has mass ' $M$ ' and it oscillates freely with amplitude ' $A$ '. At extreme position, its potential energy is

A particle performing S.H.M. starts from equilibrium position and its time period is 12 second. After 2 seconds its velocity is $\pi \mathrm{m} / \mathrm{s}$. Amplitude of the oscillation is $\left[\sin 30^{\circ}=\cos 60^{\circ}=0 \cdot 5, \sin 60^{\circ}=\cos 30^{\circ}=\sqrt{3} / 2\right]$

A particle performs linear S.H.M. at a particular instant, velocity of the particle is ' $u$ ' and acceleration is ' $\mathrm{a}_1$ ' while at another instant velocity is ' V ' and acceleration is ' $a_2$ ' $\left(0

A particle starts oscillating simple harmonically from its equilibrium position with time period ' T '. What is the ratio of potential energy to kinetic energy of the particle at time $t=\frac{T}{12}$ ? $$\left(\sin \left(\frac{\pi}{6}\right)=\frac{1}{2}\right)$$

A particle performs linear S.H.M. When the displacement of the particle from mean position is 3 cm and 4 cm , corresponding velocities are $8 \mathrm{~cm} / \mathrm{s}$ and $6 \mathrm{~cm} / \mathrm{s}$ respectively. Its periodic time is

A simple pendulum of length ' $l$ ' has a brass bob attached at its lower end. It's period is ' T '. A steel bob of the same size, having density ' $x$ ' times that of brass, replaces the brass bob. Its length is then so changed that the period becomes ' 2 T '. What is the new length?

A particle performing S.H.M. with maximum velocity ' $V$ '. If the amplitude double and periodic time is made, $\left(\frac{1}{3}\right)^{\text {rd }}$ then the maximum velocity is

Let ' $l_1$ ' be the length of simple pendulum. Its length changes to ' $l_2$ ' to increase the periodic time by $20 \%$. The ratio $\frac{l_2}{l_1}=$

A particle is executing a linear simple harmonic motion. Let ' $\mathrm{V}_1$ ' and ' $\mathrm{V}_2$ ' are its speed at distance ' $x_1$ ' and ' $x_2$ ' from the equilibrium position. The amplitude of oscillation is

In S.H.M. the displacement of a particle at an instant is $Y=A \cos 30^{\circ}$, where $A=40 \mathrm{~cm}$ and kinetic energy is 200 J . If force constant is $1 \times 10^{\times} \mathrm{N} / \mathrm{m}$, then x will be $\left(\cos 30^{\circ}=\sqrt{3} / 2\right)$

A particle is performing S.H.M. with an amplitude 4 cm . At the mean position the velocity of the particle is $12 \mathrm{~cm} / \mathrm{s}$. When the speed of the particle becomes $6 \mathrm{~cm} / \mathrm{s}$, the distance of the particle from mean position is

The maximum velocity and maximum acceleration of a particle performing a linear S.H.M. is ' $\alpha$ ' and ' $\beta$ ' respectively. Then the path length of the particle is

A mass ' $m$ ' attached to a spring oscillates with a period of 3 second. If the mass is increased by 0.6 kg , the period increases by 3 second. The initial mass ' $m$ ' is equal to

The velocity of particle executing S.H.M. varies with displacement $(\mathrm{x})$ as $4 \mathrm{~V}^2=50-\mathrm{x}^2$. The time period of oscillation is $\frac{x}{7}$ second. The value of ' $x$ ' is (Take $\pi=\frac{22}{7}$)

A simple pendulum of length $l_1$ has time period $\mathrm{T}_1$. Another simple pendulum of length $l_2\left(l_1>l_2\right)$ has time period $T_2$. Then the time period of the pendulum of length $\left(l_1-l_2\right)$ will be

Two bodies A and B of equal mass are suspended from two separate massless springs of spring constants $\mathrm{K}_1$ and $\mathrm{K}_2$ respectively. The two bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitude of $B$ to that of $A$ is

The period of a simple pendulum gets doubled when

Frequency of a particle performing S.H.M. is 10 Hz . The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right)$

When a particle in linear S.H.M. completes two oscillations, its phase increases by

A small sphere oscillates simple harmonically in a watch glass whose radius of curvature is 1.6 m . The period of oscillation of the sphere in second is (acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

A tube of uniform bore of cross-sectional area ' $A$ ' has been set up vertically with open end facing up. Now ' $M$ ' gram of a liquid of density ' $d$ ' is poured into it. The column of liquid in this tube will oscillate with a period ' T ', which is equal to [ $g=$ acceleration due to gravity]

A spring has a certain mass suspended from it and its period of vertical oscillations is $T_1$. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillations is now $\mathrm{T}_2$. The ratio of $T_2 / T_1$ is

For a body performing simple harmonic motion, its potential energy is $\mathrm{E}_{\mathrm{x}}$ at displacement x and $\mathrm{E}_{\mathrm{y}}$ at displacement y from mean position. The potential energy $E_0$ at displacement $(x+y)$ is

The displacement of a particle performing S.H.M. is given by $Y=A \cos [\pi(t+\phi)]$. If at $\mathrm{t}=0$, the displacement is $\mathrm{y}=2 \mathrm{~cm}$ and velocity is $2 \pi \mathrm{~cm} / \mathrm{s}$, the value of amplitude $A$ in cm is

A particle is performing simple harmonic motion and if the oscillations are Camped oscillations then the angular frequency is given by

Choose the correct answer. When a point of suspension of pendulum is moved vertically upward with acceleration ' $a$ ', its period of oscillation

Three masses $500 \mathrm{~g}, 300 \mathrm{~g}$ and 100 g are suspended at the end of spring as shown in figure and are in equilibrium. When the 500 g mass is removed, the system oscillates with a period of 3 second. When the 300 g mass is also removed it will oscillate with a period of

A uniform circular disc of mass $$12 \mathrm{~kg}$$ is held by two identical springs. When the disc is slightly pressed down and released, it executes S.H.M. of period 2 second. The force constant of each spring is (nearly) (Take $$\pi^2=10$$ )

A light spring is suspended with mass $$m_1$$ at its lower end and its upper end fixed to a rigid support. The mass is pulled down a short distance and then released. The period of oscillation is $$T$$ second. When a mass $$m_2$$ is added to $$m_1$$ and the system is made to oscillate, the period is found to be $$\frac{3}{2} T$$. The ratio $$m_1: m_2$$ is

A block of mass '$$M$$' rests on a piston executing S.H.M. of period one second. The amplitude of oscillations, so that the mass is separated from the piston, is (acceleration due to gravity, $$\mathrm{g}=10 \mathrm{~ms}^{-2}, \pi^2=10$$ )

A simple pendulum of length '$$l$$' and a bob of mass '$$\mathrm{m}$$' is executing S.H.M. of small amplitude '$$A$$'. The maximum tension in the string will be ($$\mathrm{g}=$$ acceleration due to gravity)

The displacement of a particle executing S.H.M. is $$x=\mathrm{a} \sin (\omega t-\phi)$$. Velocity of the particle at time $$\mathrm{t}=\frac{\phi}{\omega}$$ is $$\left(\cos 0^{\circ}=1\right)$$

The bob of simple pendulum of length '$$L$$' is released from a position of small angular displacement $$\theta$$. Its linear displacement at time '$$\mathrm{t}$$' is ( $$\mathrm{g}=$$ acceleration due to gravity)

Under the influence of force $$F_1$$ the body oscillates with a period $$T_1$$ and due to another force $$F_2$$ body oscillates with period $$T_2$$. If both forces acts simultaneously, then the resultant period is (consider displacement is same in all three cases)

A mass $$M$$ is suspended from a light spring. An additional mass $$M_1$$ added extends the spring further by a distance $$x$$. Now, the combined mass will oscillate on the spring with period $$T=$$

A body of mass $$0.04 \mathrm{~kg}$$ executes simple harmonic motion (SHM) about $$\mathrm{x}=0$$ under the influence of force $$\mathrm{F}$$ as shown in graph. The period of

A simple pendulum has a time period '$$T$$' in air. Its time period when it is completely immersed in a liquid of density one eighth the density of the material of bob is

In a stationary lift, time period of a simple pendulum is '$$\mathrm{T}$$'. The lift starts accelerating downwards with acceleration $$\left(\frac{\mathrm{g}}{4}\right)$$, then the time period of the pendulum will be

A particle starts from mean position and performs S.H.M. with period 4 second. At what time its kinetic energy is $$50 \%$$ of total energy?

$$\left(\cos 45^{\circ}=\frac{1}{\sqrt{2}}\right)$$

A simple pendulum performs simple harmonic motion about $$\mathrm{x}=0$$ with an amplitude '$$\mathrm{a}$$' and time period '$$T$$'. The speed of the pendulum at $$x=\frac{a}{2}$$ is

Four massless springs whose force constants are $$2 \mathrm{~K}, 2 \mathrm{~K}, \mathrm{~K}$$ and $$2 \mathrm{~K}$$ respectively are attached to a mass $$\mathrm{M}$$ kept on a frictionless plane as shown in figure, If mass $$M$$ is displaced in horizontal direction then frequency of oscillating system is

The upper end of the spring is fixed and a mass '$$m$$' is attached to its lower end. When mass is slightly pulled down and released, it oscillates with time period 3 second. If mass '$$\mathrm{m}$$' is increased by $$1 \mathrm{~kg}$$, the time period becomes 5 second. The value of '$$\mathrm{m}$$' is (mass of spring is negligible)

For a particle executing S.H.M., its potential energy is 8 times its kinetic energy at certain displacement '$$x$$' from the mean position. If '$$A$$' is the amplitude of S.H.M the value of '$$x$$' is

The time period of a simple pendulum inside a stationary lift is '$$T$$'. When the lift starts accelerating upwards with an acceleration $$\left(\frac{\mathrm{g}}{3}\right)$$, the time period of the pendulum will be

A body is executing a linear S.H.M. Its potential energies at the displacement '$$\mathrm{x}$$' and '$$\mathrm{y}$$' are '$$\mathrm{E}_1$$' and '$$E_2$$' respectively. Its potential energy at displacement $$(\mathrm{x}+\mathrm{y})$$ will be

A simple harmonic progressive wave is represented by $$y=A \sin (100 \pi t+3 x)$$. The distance between two points on the wave at a phase difference of $$\frac{\pi}{3}$$ radian is

The amplitude of a particle executing S.H.M. is $$3 \mathrm{~cm}$$. The displacement at which its kinetic energy will be $$25 \%$$ more than the potential energy is

Two S.H.Ms. are represented by equations $$\mathrm{y}_1=0.1 \sin \left(100 \pi \mathrm{t}+\frac{\pi}{3}\right)$$ and $$\mathrm{y}_2=0.1 \cos (100 \pi \mathrm{t})$$ The phase difference between the speeds of the two particles is

A spring has a certain mass suspended from it and its period for vertical oscillations is '$$T_1$$'. The spring is now cut in to two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillations is now '$$\mathrm{T}_2$$'. The ratio $$\mathrm{T}_1 / \mathrm{T}_2$$ is

A particle is vibrating in S.H.M. with an amplitude of $$4 \mathrm{~cm}$$. At what displacement from the equilibrium position is its energy half potential and half kinetic?

A rubber ball filled with water, having a small hole is used as the bob of a simple pendulum. The time period of such a pendulum

The maximum velocity of a particle performing S.H.M. is '$$\mathrm{V}$$'. If the periodic time is made $$\left(\frac{1}{3}\right)^d$$ and the amplitude is doubled, then the new maximum velocity of the particle will be

The time taken by a particle executing simple harmonic motion of period '$$\mathrm{T}$$', to move from the mean position to half the maximum displacement is

In a medium, the phase difference between two particles separated by a distance '$$x$$' is $$\left(\frac{\pi}{5}\right)^{\text {c }}$$. If the frequency of the oscillation of particles is $$25 \mathrm{~Hz}$$ and the velocity of propagation of the waves is $$75 \mathrm{~m} / \mathrm{s}$$, then the value of $$x$$ is

A particle starts oscillating simple harmonically from its mean position with time period '$$T$$'. At time $$t=\frac{T}{12}$$, the ratio of the potential energy to kinetic energy of the particle is $$\left(\sin 30^{\circ}=\cos 60^{\circ}=0.5, \cos 30^{\circ}=\sin 60^{\circ}=\sqrt{3} / 2\right)$$

The displacement of a particle performing S.H.M. is given by $$x=5 \sin (3 t+3)$$, where $$x$$ is in $$\mathrm{cm}$$ and $$t$$ is in second. The maximum acceleration of the particle will be

Two identical springs of constant '$$\mathrm{K}$$' are connected in series and parallel in shown in figure. A mass '$$\mathrm{M}$$' is suspended from them. The ratio of their frequencies is series to parallel combination will be

A particle performing linear S.H.M. of amplitude $$0.1 \mathrm{~m}$$ has displacement $$0.02 \mathrm{~m}$$ and acceleration $$0.5 \mathrm{~m} / \mathrm{s}^2$$. The maximum velocity of the particle in $$\mathrm{m} / \mathrm{s}$$ is

A body is executing S.H.M. under the action of force having maximum magntude $$50 \mathrm{~N}$$. When its energy is half kinetic and half potential; the magnitude of the force acting on the particle is

A bob of simple pendulum of mass 'm' perform $$\mathrm{SHM}$$ with amplitude '$$\mathrm{A}$$' and period 'T'. Kinetic energy of pendulum of displacement $$x=\frac{A}{2}$$ will be

An object executes SHM along $$x$$-axis with amplitude $$0.06 \mathrm{~m}$$. At certain distance '$$\mathrm{x}$$' metre from mean position, it has kinetic energy $$10 \mathrm{~J}$$ and potential energy $$8 \mathrm{~J}$$. the distance '$$\mathrm{x}$$' will be

A body executes SHM under the action of force '$$\mathrm{F}_1$$' with time period '$$\mathrm{T}_1$$'. If the force is changed to '$$\mathrm{F_2}$$', it executes SHM with period '$$\mathrm{T_2}$$'. If both the forces '$$\mathrm{F_1}$$' and '$$\mathrm{F}_2$$' act simultaneously in the same direction on the body, its time period is

A particle performing S.H.M. when displacement is '$$x$$', the potential energy and restoring force acting on it are denoted by '$$E$$' and '$$F$$' respectively. The relation between $$x, E$$ and $$F$$ is

A body is performing S.H.M. of amplitude 'A'. The displacement of the body from a point where kinetic energy is maximum to a point where potential energy is maximum, is

A particle excuting S.H.M starts from the mean position. Its amplitude is 'A' and time period '$$\mathrm{T}$$' At what displacement its speed is one-fourth of the maximum speed?

A particle connected to the end of a spring executes S.H.M. with period '$$T_1$$'. While the corresponding period for another spring is '$$\mathrm{T}_2$$'. If the period of oscillation with two springs in series is 'T', then

'$$n$$' waves are produced on a string in 1 second. When the radius of the string is doubled, keeping tension same, the number of waves produced in 1 second for the same harmonic will be

A body of mass '$$m$$' performs linear S.H.M. given by equation $$x=P \sin \omega t+Q \sin \left(\omega t+\frac{\pi}{2}\right)$$. The total energy of the particle at any instant is

A mass $$0.4 \mathrm{~kg}$$ performs S.H.M. with a frequency $$\frac{16}{\pi} \mathrm{Hz}$$. At a certain displacement it has kinetic energy $$2 \mathrm{~J}$$ and potential energy $$1.2 \mathrm{~J}$$. The amplitude of oscillation is

If the amplitude of linear S.H.M. is decreased then

A child is sitting on a swing which performs S.H.M. It has minimum and maximum heights from ground $$0.75 \mathrm{~cm}$$ and $$2 \mathrm{~m}$$ respectively. Its maximum speed will be $$\left[\mathrm{g}=10 \frac{\mathrm{m}}{\mathrm{s}^2}\right]$$

A pendulum clock is running fast. To correct its time, we should

A particle is performing S.H.M. with maximum velocity '$$v$$'. If the amplitude is tripled and periodic time is doubled then maximum velocity will be

A particle executes S.H.M. of period $$\frac{2 \pi}{\sqrt{3}}$$ second along a straight line $$4 \mathrm{~cm}$$ long. The displacement of the particle at which the velocity is numerically equal to the acceleration is

A particle is suspended from a vertical spring which is executing S.H.M. of frequency $$5 \mathrm{~Hz}$$. The spring is unstretched at the highest point of oscillation. Maximum speed of the particle is $$(\mathrm{g} =10 \mathrm{~m} / \mathrm{s}^2)$$

A body performs S.H.M. under the action of force '$$\mathrm{F}_1$$' with period '$$\mathrm{T}_1$$' second. If the force is changed to '$$\mathrm{F}_2$$' it performs S.H.M. with period '$$\mathrm{T_2}$$' second. If both forces '$$\mathrm{F_1}$$' and '$$\mathrm{F_2}$$' act simultaneously in the same direction on the body, the period in second will be

A mass '$$\mathrm{m}_1$$' is suspended from a spring of negligible mass. A spring is pulled slightly in downward direction and released, mass performs S.H.M. of period '$$\mathrm{T}_1$$'. If the mass is increased by '$$\mathrm{m}_2$$', the time period becomes '$$\mathrm{T}_2$$'. The ratio $$\frac{\mathrm{m}_2}{\mathrm{~m}_1}$$ is

Two particles $$\mathrm{P}$$ and $$\mathrm{Q}$$ performs S.H.M. of same amplitude and frequency along the same straight line. At a particular instant, maximum distance between two particles is $$\sqrt{2}$$ a. The initial phase difference between them is

$$\left[\sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)=\cos ^{-1}\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi}{4}\right]$$

A particle of mass 5kg is executing S.H.M. with an amplitude 0.3 m and time period $$\frac{\pi}{5}$$s. The maximum value of the force acting on the particle is

Two bodies $A$ and $B$ of equal mass are suspended from two separate massles springs of force constant $k_1$ and $k_2$, respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body $A$ to that of body $B$ is

A bob of a simple pendulum has mass $m$ and is oscillating with an amplitude $a$. If the length of the pendulum is $L$, then the maximum tension in the string is $\left[\cos 0^{\circ}=1\right.$, $g=$ acceleration due to gravity]

A body of mass 64 g is made to oscillate turn by turn on two different springs $A$ and $B$. Spring $A$ and $B$ has force constant $4 \frac{\mathrm{~N}}{\mathrm{~m}}$ and $16 \frac{\mathrm{~N}}{\mathrm{~m}}$ respectively. If $T_1$ and $T_2$ are period of oscillations of springs $A$ and $B$ respectively, then $\frac{T_1+T_2}{T_1-T_2}$ will be

The damping force of an oscillator is directly proportional to the velocity. The unit of constant of proportionality is

A particle performs simple harmonic motion with period of 3 s . The time taken by it to cover a distance equal to half the amplitude from mean position is [$$\sin 30^{\circ}=0.5$$]

A simple pendulum of length $$I$$ has a bob of mass $$m$$. It executes SHM of small amplitude A. The maximum tension in the string is ($$g=$$ acceleration due to gravity)

A block of mass $$m$$ attached to one end of the vertical spring produces extension $$x$$. If the block is pulled and released, the periodic time of oscillation is

A simple pendulum of length $$L$$ has mass $$m$$ and it oscillates freely with amplitude $$A$$. At extreme position, its potential energy is ($$g=$$ acceleration due to gravity)

For a particle performing SHM when displacement is $$x$$, the potential energy and restoring force acting on it is denoted by $$E$$ and $$F$$, respectively. The relation between $$x, E$$ and $$F$$ is

A person measures a time period of a simple pendulum inside a stationary lift and finds it to be $T$. If the lift starts accelerating upwards with an acceleration $\left(\frac{g}{3}\right)$, the time period of the pendulum will be

In damped SHM, the SI unit of damping constant is

The total energy of a simple harmonic oscillaior is proportional to

A particle is performing a linear simple harmonic motion of amplitude ' $A$ '. When it is midway between its mean and extreme position, the magnitudes of its velocity and acceleration are equal. What is the periodic time of the motion?

Two pendulums begin to swing simultaneously. The first pendulum makes nine full oscillations when the other makes seven. The ratio of the lengths of the two pendulums is

If ' $x$ ', $v$ ' and ' $a$ ' denote the displacement, velocity and acceleration of a particle respectively executing SHM of periodic time $h$ then which one of the following does not change with time?

The quantity which does not vary periodically for a particle performing SHM is

A particle executes the simple harmonic motion with an amplitude ' $A$ '. The distance travelled by it in one periodic time is