1
GATE ECE 2003
MCQ (Single Correct Answer)
+2
-0.6
The current flowing through the resistance R in the circuit in figure has the form
P cos 4t, where P is
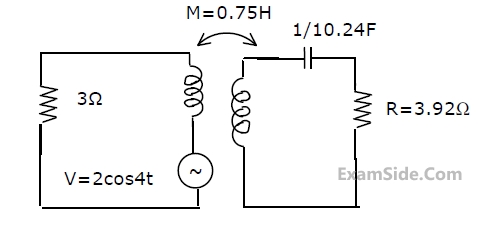

2
GATE ECE 2003
MCQ (Single Correct Answer)
+2
-0.6
An input voltage $$v(t)$$ $$ = 10\sqrt 2 \,\,\cos \,\,\left( {t + {{10}^0}} \right) + 10\sqrt 5 \,\,\cos \left( {2t + {{10}^0}} \right)\,\,V$$ is applied to a series combination of resistance $$L = 1H$$. the resulting steady - state current $$i(t)$$ in ampere is
3
GATE ECE 2002
MCQ (Single Correct Answer)
+2
-0.6
If the 3-phase balanced source in Fig. delivers 1500 W at a leading power
factor of 0.844, then the value of ZL (in ohm) is approximately
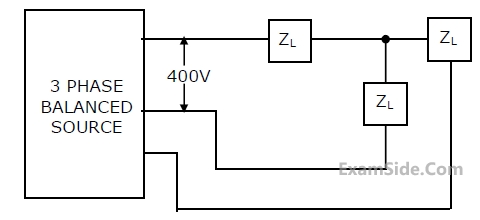

4
GATE ECE 2001
MCQ (Single Correct Answer)
+2
-0.6
When the angular frequency $$\omega $$ in Fig. is varied from $$0$$ to $$\infty $$ the locus of the current phasor $${{\rm I}_2}$$ is given by
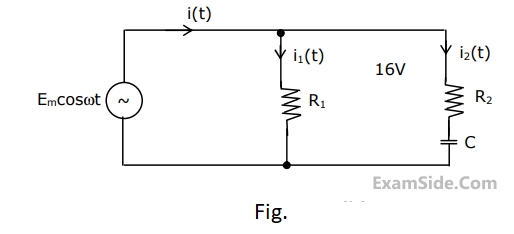
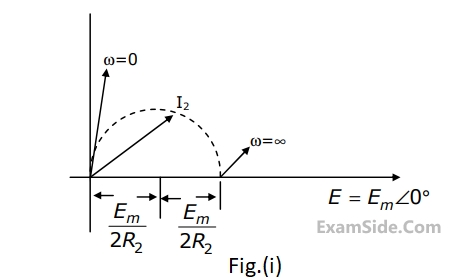
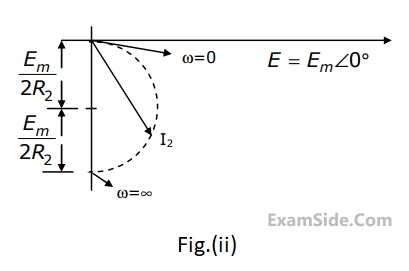
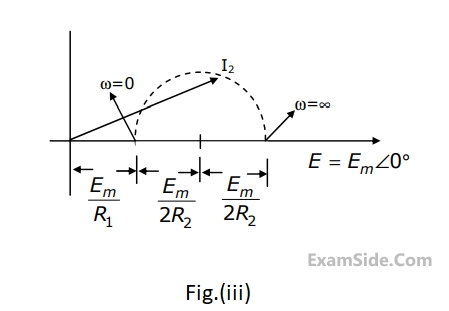
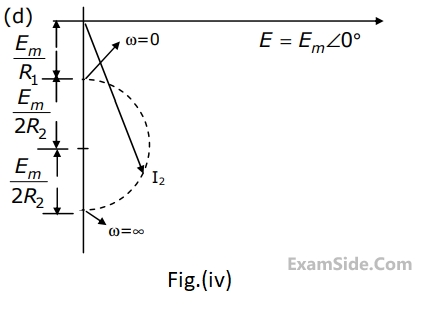





Questions Asked from Sinusoidal Steady State Response (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2025 (1)
GATE ECE 2022 (2)
GATE ECE 2018 (1)
GATE ECE 2017 Set 1 (2)
GATE ECE 2016 Set 1 (2)
GATE ECE 2015 Set 1 (2)
GATE ECE 2015 Set 3 (1)
GATE ECE 2014 Set 4 (1)
GATE ECE 2014 Set 3 (1)
GATE ECE 2014 Set 2 (1)
GATE ECE 2014 Set 1 (3)
GATE ECE 2010 (1)
GATE ECE 2009 (1)
GATE ECE 2007 (2)
GATE ECE 2005 (1)
GATE ECE 2004 (2)
GATE ECE 2003 (2)
GATE ECE 2002 (1)
GATE ECE 2001 (1)
GATE ECE 2000 (1)
GATE ECE 1993 (1)
GATE ECE 1992 (1)
GATE ECE 1991 (1)
GATE ECE 1990 (2)
GATE ECE 1989 (1)
GATE ECE 1987 (1)
GATE ECE Subjects
Network Theory
Control Systems
Electronic Devices and VLSI
Analog Circuits
Digital Circuits
Microprocessors
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Communications
Electromagnetics
General Aptitude