1
GATE ECE 2000
Subjective
+5
-0
For the circuit in Fig., write the state equations using vc
and iL as state variables.
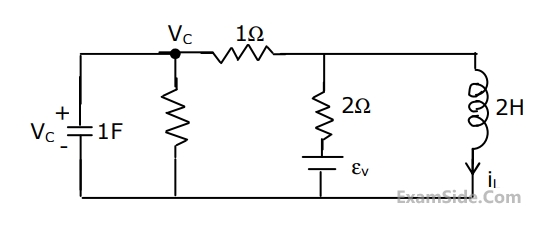

2
GATE ECE 1997
Subjective
+5
-0
 For the circuit shown in Fig. choose state variables $$X_1,\;X_2,\;X_3$$ to be $$i_{L1}\left(t\right),\;v_{C2}\left(t\right),\;i_{L3}\left(t\right)$$
For the circuit shown in Fig. choose state variables $$X_1,\;X_2,\;X_3$$ to be $$i_{L1}\left(t\right),\;v_{C2}\left(t\right),\;i_{L3}\left(t\right)$$
(a) Write the state equations
$$$\begin{bmatrix}{\dot X}_1\\{\dot X}_2\\{\dot X}_3\end{bmatrix}\;=\;A\;\begin{bmatrix}X_1\\X_2\\X_3\end{bmatrix}\;+\;B\left[e\left(t\right)\right]$$$(b) If e(t) = 0, t $$\geq$$ 0, $$i_{L1}\left(0\right)\;=\;0,\;v_{C2}\left(0\right)\;=\;0,\;i_{L3}\left(0\right)\;=\;1A,$$ then what would the total energy dissipated in the registors in the interval $$\left(0,\infty\right)$$ be
3
GATE ECE 1996
Subjective
+5
-0
Refer to the circuit shown in Fig.
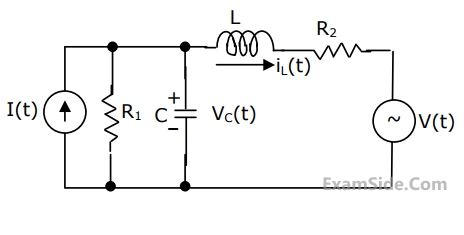 Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
 Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].Questions Asked from State Equations For Networks (Marks 5)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Network Theory
Control Systems
Electronic Devices and VLSI
Analog Circuits
Digital Circuits
Microprocessors
Signals and Systems
Representation of Continuous Time Signal Fourier Series Discrete Time Signal Fourier Series Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Transmission of Signal Through Continuous Time LTI Systems Discrete Time Linear Time Invariant Systems Sampling Continuous Time Signal Laplace Transform Discrete Fourier Transform and Fast Fourier Transform Transmission of Signal Through Discrete Time Lti Systems Miscellaneous Fourier Transform
Communications
Electromagnetics
General Aptitude