The transfer function of a compensator is given as $${G_C}(s) = {{s + a} \over {s + b}}.$$

$${G_C}(s)$$ is a lead compensator if

The transfer function of a compensator is given as $${G_C}(s) = {{s + a} \over {s + b}}.$$

The phase of the above lead compensator is maximum at

A unity negative feedback closed loop system has a plant with the transfer function $$G(s) = {1 \over {{s^2} + 2s + 2}}$$ and a controller $${G_c}(s)$$ in the feed forward path. For a unit set input, the transfer function of the controller that gives minimum steady sate error is

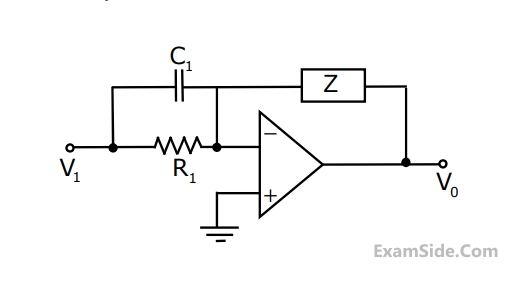
Group I gives two possible choices for the impedance Z in the diagram. The circuit elements in Z satisfy the condition $${R_2}{C_2} > {R_1}{C_{1.}}$$ The transfer $${\textstyle{{{V_0}} \over {{V_1}}}}$$ function represents a kind of controller. Match the impedances in Group I with the types of controllers in Group II. Group - I

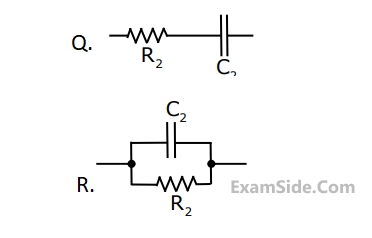
Group - II
1. PID controller
2. Lead compensator
3. Lag compensator