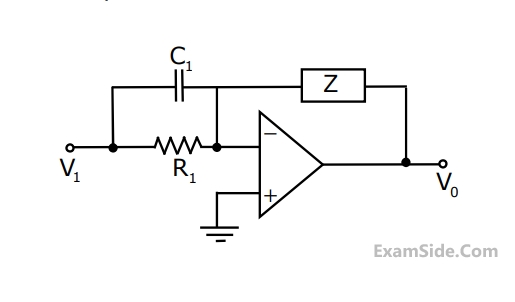
Group I gives two possible choices for the impedance Z in the diagram. The circuit elements in Z satisfy the condition $${R_2}{C_2} > {R_1}{C_{1.}}$$ The transfer $${\textstyle{{{V_0}} \over {{V_1}}}}$$ function represents a kind of controller. Match the impedances in Group I with the types of controllers in Group II. Group - I

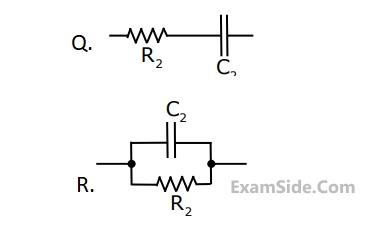
Group - II
1. PID controller
2. Lead compensator
3. Lag compensator

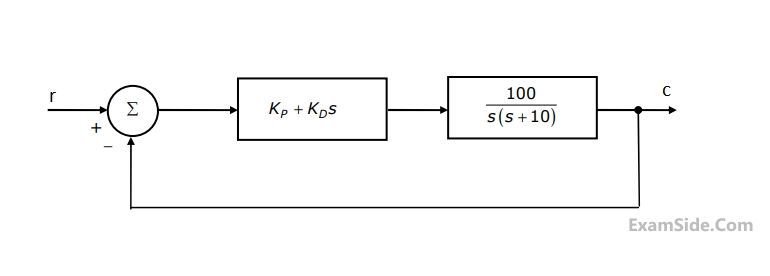
A control system with a PD controller is shown in the figure. If the velocity error constant $${K_v} = 1000$$ and the damping ratio $$\zeta = 0.5,$$ then the values of $${K_P}$$ and $${K_D}$$ are

The open-loop transfer function of a plant is given as $$G(s) = {1 \over {{s^2} - 1}}.$$ If the plant is operated in a unity feedback configuration, then the lead compensator that can stabilize this control system is

A double integrator plant, $$G(s) = {K \over {{s^2}}},H(s) = 1$$ is to be compensated to achieve the damping ratio $$\zeta = 0.5$$ and an undamped natural frequency, $${\omega _n} = 5$$ rad/sec. Which one of the following compensator $${G_c}(s)$$ will be suitable?