The circuit is given in figure.Assume that the switch S is in position 1 for a long time and thrown to position 2 at t = 0.

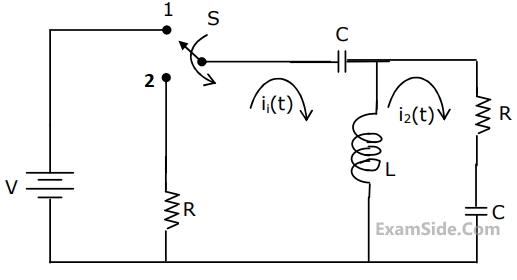
I₁(s) and I₂(s) are the Laplace transforms of i₁(t) and i₂(t) respectively. The equations for the loop currents I₁(s) and I₂(s) for the circuit shown in figure, after the switch is brought from position 1 to position 2 at t = 0, are

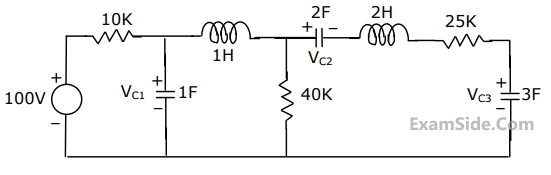
The voltage V_C1, V_C2 and V_C3 across the capacitors in the circuit in Fig., under steady state, are respectively

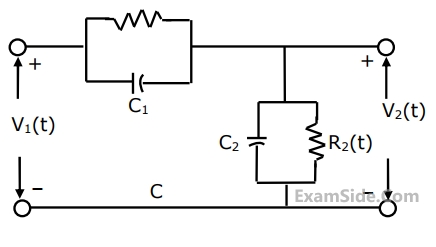
For the compensated attenuator of figure, the impulse response under the condition $$R_1C_1\;=\;R_2C_2$$ is:

If the Laplace transform of the voltage across a capacitor of value of $$\frac12\;\mathrm F$$ is $$V_C\;\left(s\right)\;=\;\frac{s\;+\;1}{s^3\;+\;s^2\;+\;s\;+\;1}$$ , the value of the current through the capacitor at t = 0⁺ is