GATE ECE 2003 | Transient Response Question 30 | Network Theory

GATE ECE 2003

MCQ (Single Correct Answer)

-0.6

The circuit is given in figure.Assume that the switch S is in position 1 for a long time and thrown to position 2 at t = 0.

GATE ECE 2003 Network Theory - Transient Response Question 32 English

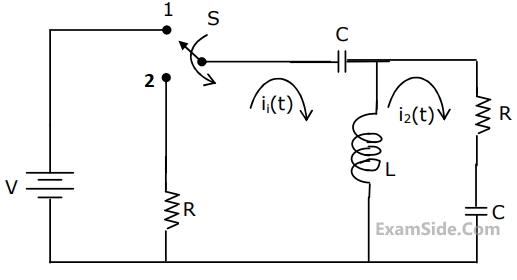
At t = 0⁺, the current i₁ is

$$\frac{-\mathrm V}{2\mathrm R}$$

$$\frac{-\mathrm V}{\mathrm R}$$

$$\frac{-\mathrm V}{4\mathrm R}$$

zero

GATE ECE 2003

MCQ (Single Correct Answer)

-0.6

The circuit is given in figure.Assume that the switch S is in position 1 for a long time and thrown to position 2 at t = 0.

GATE ECE 2003 Network Theory - Transient Response Question 31 English

I₁(s) and I₂(s) are the Laplace transforms of i₁(t) and i₂(t) respectively. The equations for the loop currents I₁(s) and I₂(s) for the circuit shown in figure, after the switch is brought from position 1 to position 2 at t = 0, are

GATE ECE 2003 Network Theory - Transient Response Question 31 English Option 1

GATE ECE 2003 Network Theory - Transient Response Question 31 English Option 2

GATE ECE 2003 Network Theory - Transient Response Question 31 English Option 3

GATE ECE 2003 Network Theory - Transient Response Question 31 English Option 4

GATE ECE 1996

MCQ (Single Correct Answer)

-0.6

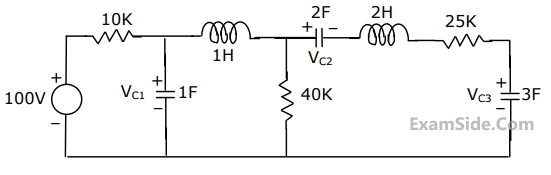
The voltage V_C1, V_C2 and V_C3 across the capacitors in the circuit in Fig., under steady state, are respectively

GATE ECE 1996 Network Theory - Transient Response Question 33 English

80 V, 32 V, 48 V

80 V, 48 V, 32 V

20 V, 8V, 12 V

20 V, 12 V, 8 V

GATE ECE 1992

MCQ (Single Correct Answer)

-0.6

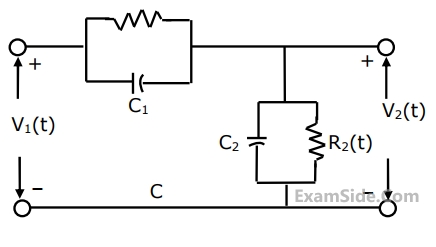
For the compensated attenuator of figure, the impulse response under the condition $$R_1C_1\;=\;R_2C_2$$ is:

GATE ECE 1992 Network Theory - Transient Response Question 34 English

$$\frac{{\mathrm R}_2}{{\mathrm R}_1\;+\;{\mathrm R}_2}\left[1\;-\;\mathrm e^\frac1{{\mathrm R}_1{\mathrm C}_1}\right]\mathrm u\left(\mathrm t\right)$$

$$\frac{{\mathrm R}_2}{{\mathrm R}_1\;+\;{\mathrm R}_2}\mathrm\delta\left(\mathrm t\right)$$

$$\frac{{\mathrm R}_2}{{\mathrm R}_1\;+\;{\mathrm R}_2}\mathrm u\left(\mathrm t\right)$$

$$\frac{{\mathrm R}_2}{{\mathrm R}_1\;+\;{\mathrm R}_2}\mathrm e^\frac1{{\mathrm R}_1{\mathrm C}_1}\mathrm u\left(\mathrm t\right)$$

PREVIOUS NEXT