1
GATE ME 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Maximize $$\,\,\,\,Z = 15{x_1} + 20{x_2}$$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
The above linear programming problem has
2
GATE ME 2016 Set 3
Numerical
+2
-0
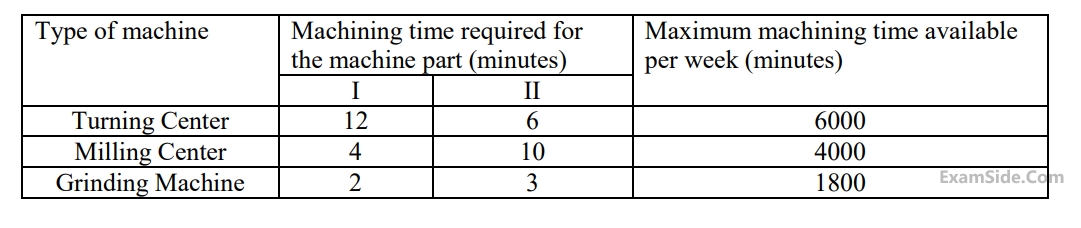
A firm uses a turning center, a milling center and a grinding machine to produce two parts. The table below provides the
machining time required for each part and the maximum machining time available on each machine. The profit per unit on parts $${\rm I}$$ and $${\rm II}$$ are Rs. $$40$$ and Rs. $$100,$$ respectively. The maximum profit per week of the firm is Rs. _______________

Your input ____
3
GATE ME 2015 Set 3
MCQ (Single Correct Answer)
+2
-0.6
For the linear programming problem:
$$\eqalign{ & Maximize\,\,\,\,\,Z = 3{x_1} + 2{x_2} \cr & Subject\,\,to\,\,\,\, - 2{x_1} + 3{x_2} \le 9 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - 5{x_2} \ge - 20 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
$$\eqalign{ & Maximize\,\,\,\,\,Z = 3{x_1} + 2{x_2} \cr & Subject\,\,to\,\,\,\, - 2{x_1} + 3{x_2} \le 9 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - 5{x_2} \ge - 20 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
The above problem has
4
GATE ME 2014 Set 3
Numerical
+2
-0
Consider an objective function $$Z\left( {{x_1},{x_2}} \right) = 3{x_1} + 9{x_2}$$ and the constraints
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
The maximum value of the objective function is ________________.
Your input ____
Questions Asked from Linear Programming (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME Subjects
Engineering Mechanics
Strength of Materials
Theory of Machines
Engineering Mathematics
Machine Design
Fluid Mechanics
Turbo Machinery
Heat Transfer
Thermodynamics
Production Engineering
Industrial Engineering
General Aptitude